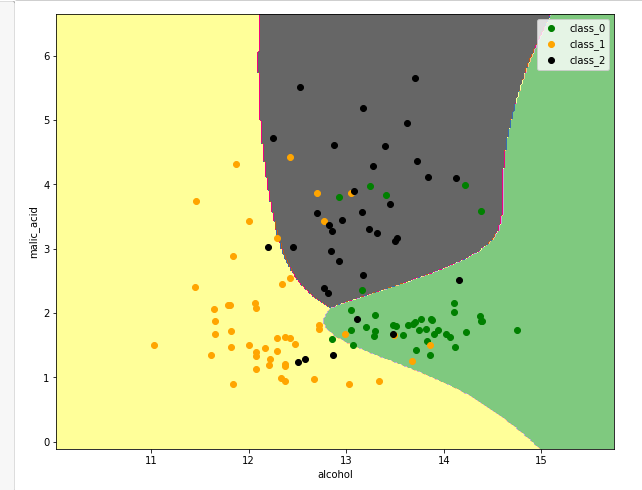
Видим, что картина поменялась. Возможно, эта картина более адекватная. Судя по метрике, она "угадывает на валидации" немножко лучше, отделяет классы друг от друга, и можно сделать вывод, что для данной задачи два скрытых слоя – это слишком много, это переусложнение, и хватает всего одного скрытого слоя, даже более того: кажется, что от уменьшения сложности нейронной сети мы выигрываем в качестве.



import torch

import random

import numpy as np

##

random.seed(0)

np.random.seed(0)

torch.manual_seed(0)

torch.cuda.manual_seed(0)

torch.backends.cudnn.deterministic = True

##
import sklearn.datasets

wine = sklearn.datasets.load_wine()

wine.data.shape

##


from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(

wine.data[:, :2],

wine.target,

test_size=0.3,

shuffle=True)

X_train = torch.FloatTensor(X_train)

X_test = torch.FloatTensor(X_test)

y_train = torch.LongTensor(y_train)

y_test = torch.LongTensor(y_test)

##

class WineNet(torch.nn.Module):

def __init__(self, n_hidden_neurons):

super(WineNet, self).__init__()

self.fc1 = torch.nn.Linear(2, n_hidden_neurons)

self.activ1 = torch.nn.Sigmoid()

self.fc2 = torch.nn.Linear(n_hidden_neurons, n_hidden_neurons)

self.activ2 = torch.nn.Sigmoid()

self.fc3 = torch.nn.Linear(n_hidden_neurons, 3)

self.sm = torch.nn.Softmax(dim=1)

def forward(self, x):

x = self.fc1(x)

x = self.activ1(x)

x = self.fc2(x)

x = self.activ2(x)

x = self.fc3(x)

return x
def inference(self, x):

x = self.forward(x)

x = self.sm(x)

return x

wine_net = WineNet(5)

##

##

loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(wine_net.parameters(),

lr=1.0e-3)
##

batch_size = 10
for epoch in range(5000):

order = np.random.permutation(len(X_train))

for start_index in range(0, len(X_train), batch_size):

optimizer.zero_grad()

batch_indexes = order[start_index:start_index+batch_size]

x_batch = X_train[batch_indexes]

y_batch = y_train[batch_indexes]

preds = wine_net.forward(x_batch)

loss_value = loss(preds, y_batch)

loss_value.backward()

optimizer.step()

if epoch % 100 == 0:

test_preds = wine_net.forward(X_test)

---

test_preds = test_preds.argmax(dim=1)

print((test_preds == y_test).float().mean())
##
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['figure.figsize'] = (10, 8)
n_classes = 3

plot_colors = ['g', 'orange', 'black']

plot_step = 0.02
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1

y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = torch.meshgrid(torch.arange(x_min, x_max, plot_step),

torch.arange(y_min, y_max, plot_step))
preds = wine_net.inference(

torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1))
preds_class = preds.data.numpy().argmax(axis=1)

preds_class = preds_class.reshape(xx.shape)

plt.contourf(xx, yy, preds_class, cmap='Accent')
for i, color in zip(range(n_classes), plot_colors):

indexes = np.where(y_train == i)

plt.scatter(X_train[indexes, 0],

X_train[indexes, 1],

c=color,

label=wine.target_names[i],

cmap='Accent')

plt.xlabel(wine.feature_names[0])

plt.ylabel(wine.feature_names[1])

plt.legend()

##
Задание на лабораторную работу

1. 
   Изучить понятие кросс-энтропии и Softmax.
   
2. 
   Исследовать нейронную сеть при заданных начальных параметрах (см. таблицу). Найти минимальное значение n_hidden_neurons, при котором сеть дает неудовлетворительные результаты, т.е. обучение невозможно.
   
3. 
   Исследовать зависимость точности распознавания от количества нейронов в скрытом слое, количества слоев, метода активации.
   
4. 
   При каком значении test_size сеть предсказывает хуже, чем Base Rate (BaseRate –это вероятность самого многочисленного класса в исходных данных)? И какой Base Rate у датасета вин?
   

Примечание: самый многочисленный класс датасета – первый.

Base Rate = len(wine.target[wine.target == 1]) / len(wine.target)

5. 
   Исследовать зависимость времени обучения от размера батча.
   

Таблица. Начальные значения гиперпараметров нейронной сети

Вариант	Метод оптимизации	Число нейронов в скрытом слое n_hidden_neurons	Шаг градиентного спуска lr
0	ADAM	10	0.01
1	ADAM	20	0.001
2	ADAM	30	0.01
3	ADAM	40	0.001
4	ADAM	5	0.01
5	SGD	10	0.001
6	SGD	20	0.01
7	SGD	30	0.001
8	SGD	40	0.01
9	SGD	50	0.001

---

Содержание отчета

1. 
   Титульный лист
   
2. 
   Цель работы, постановка задачи исследования.
   
3. 
   Описание методики исследования.
   
4. 
   Результаты исследования в соответствии с заданием.
   
5. 
   Выводы по работе.
   

---

Смотрите также файлы

• Диагностический инструментарий Адаптация первоклассников к обучению в школе Методика Что мне нравится в школе.docx

• Контрольная работа по географии по теме литосфера моу семибратовская сош учитель географии.doc

• Минимизация логических выражений.docx

• Физика 2тосан тыызды блімі бойынша жиынты баалау.docx

• Білім беру йымыны атауы 66 азырт.docx