Файл: А. Д. Швецова Специальность 15. 02. 10 Мехатроника и мобильная робототехника (по отраслям).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Пермского края
Краевое государственное автономное профессиональное
образовательное учреждение
«Пермский авиационный техникум им. А.Д. Швецова»
Специальность 15.02.10 «Мехатроника и мобильная робототехника (по отраслям)»

ОТЧЁТ ПО ЛАБАЛАТОРНЫМ РАБОТАМ
по дисциплине: Основы Автоматического Управления
Выполнил студенты гр. МХ-20-1
Ю.С. Колобов А.В.Старцев .
(И.О. Фамилия)
(номер зачётной книжки)
(дата, подпись)
Проверил _ преподаватель___
(должность)
А.В. Могильников
(И.О. Фамилия)
(оценка)
(дата, подпись)
2022 г.
С
 одержание
одержаниеОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1
Цель работы: изучить временные характеристики систем, познакомиться с интерфейсом и выполнить задания в программе Matlab.
Задание 1
Создать график ступенчатого входного воздействия
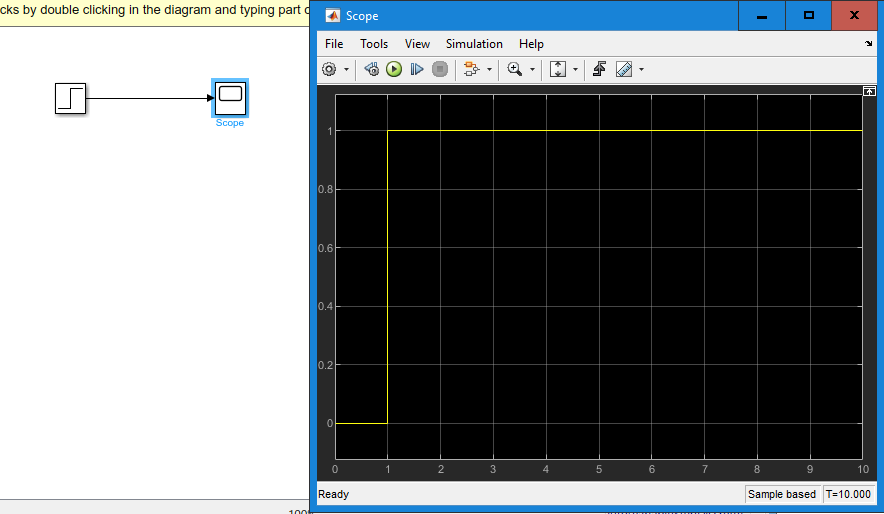
Рисунок 1 График ступенчатого входного воздействия
Задание 2
Создать график придаточной функции апериодического звена
Формула придаточной функции апериодического звена
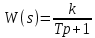
K- коэффициент усиления
T- постоянная времени
p- оператор Лапласа
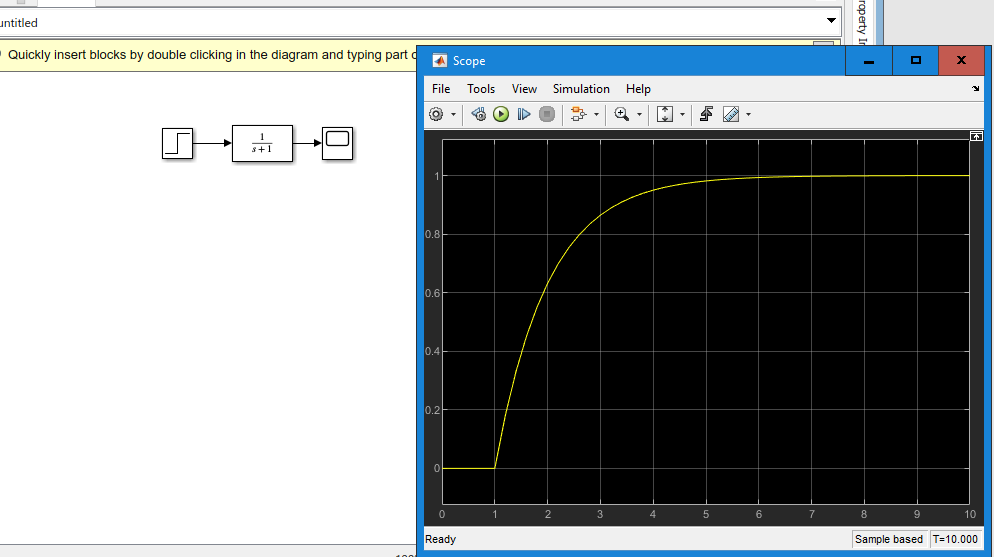
Рисунок 2 График придаточной функции апериодического звена
Изменить задержку при при ступенчатой входной характиристике с 1 на число приблеженное к 0.
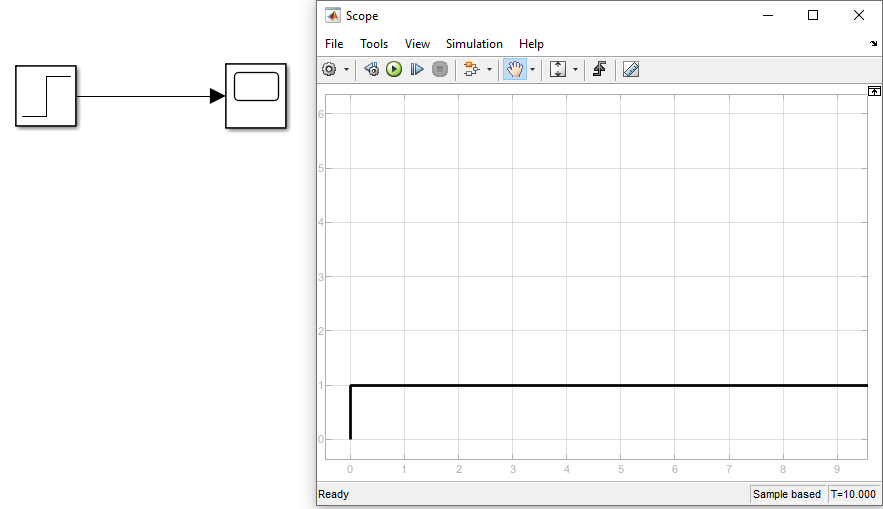
Рисунок 3 График ступенчатого входного воздействия с задержкой приближенной к 0
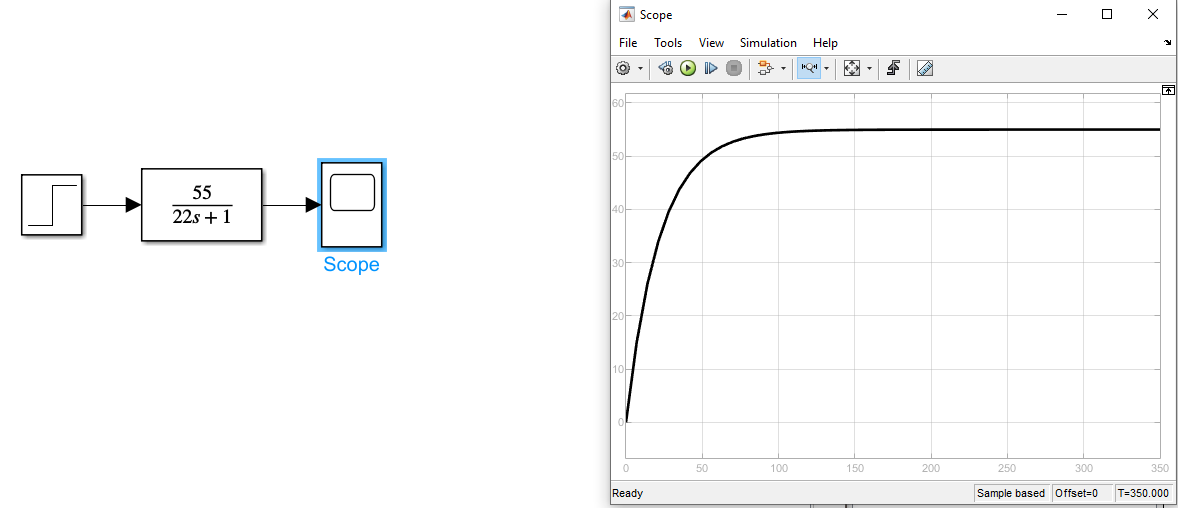
Рисунок 4 График придаточной функции апериодического звена с задержкой приближенной к 0 K=55 и T=22
Задание 3
Создать графики передаточных функций апериодического звена с изменением данных
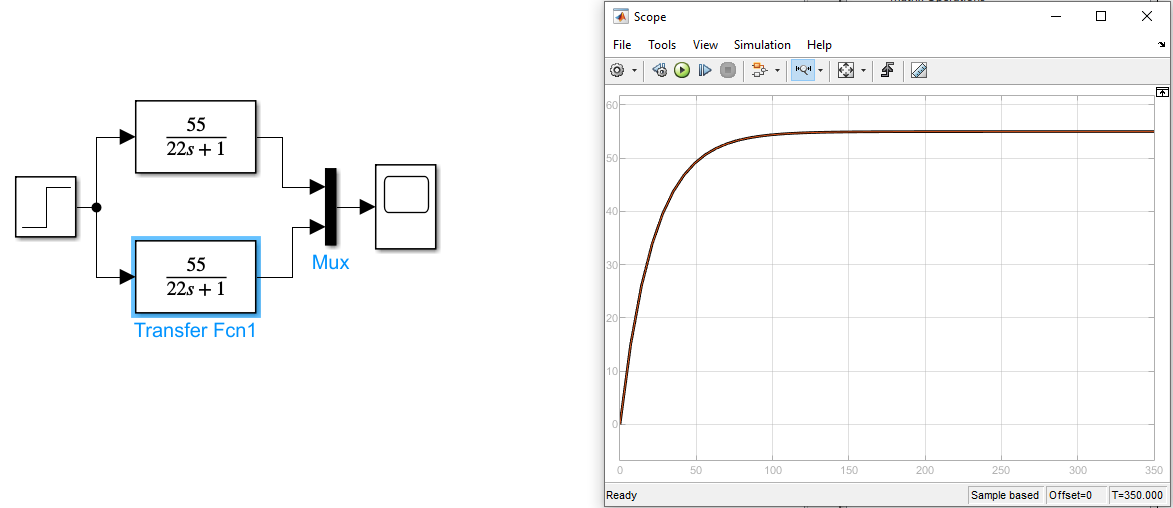
Рисунок 5 Графики передаточных функций апериодического звена K1=K2=55 T1=T2=22
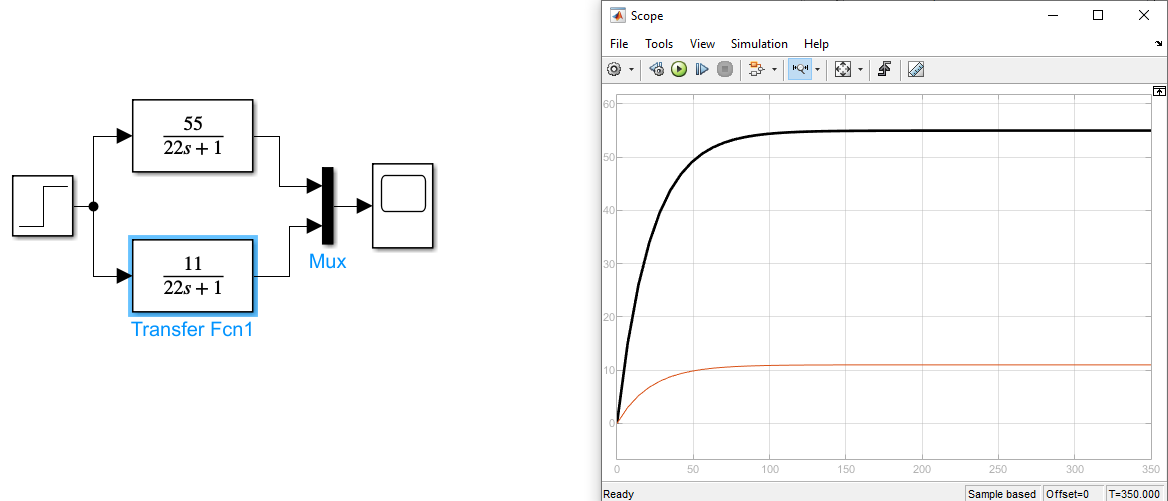
Рисунок 6 Графики передаточных функций апериодического звена с изменением коэффициента усиления
Красный график K1=11, черный – K2=55
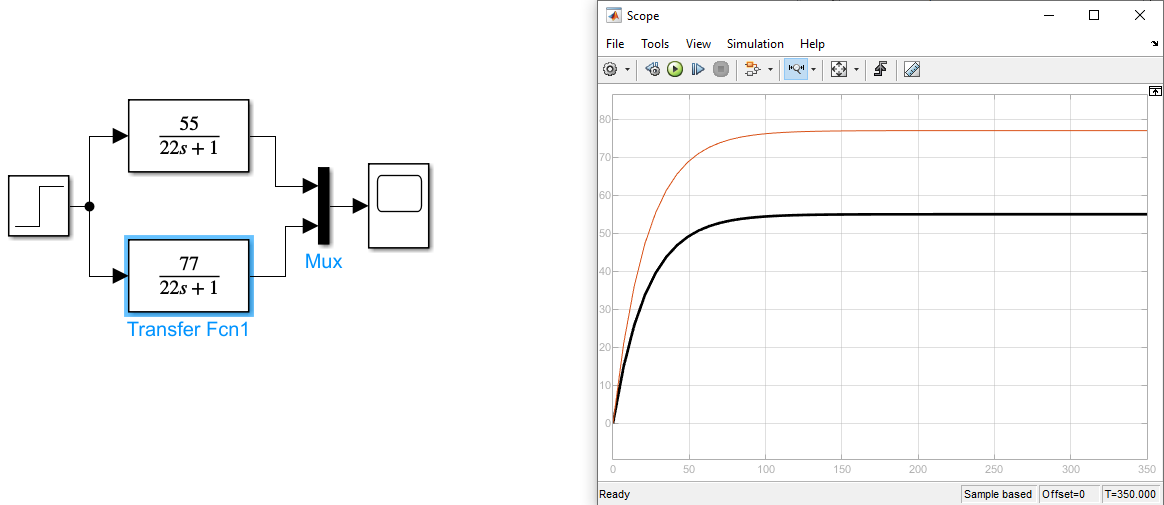
Рисунок 7 Графики передаточных функций апериодического звена с изменением коэффициента усиления
Красный график K1=77, черный - K2=55
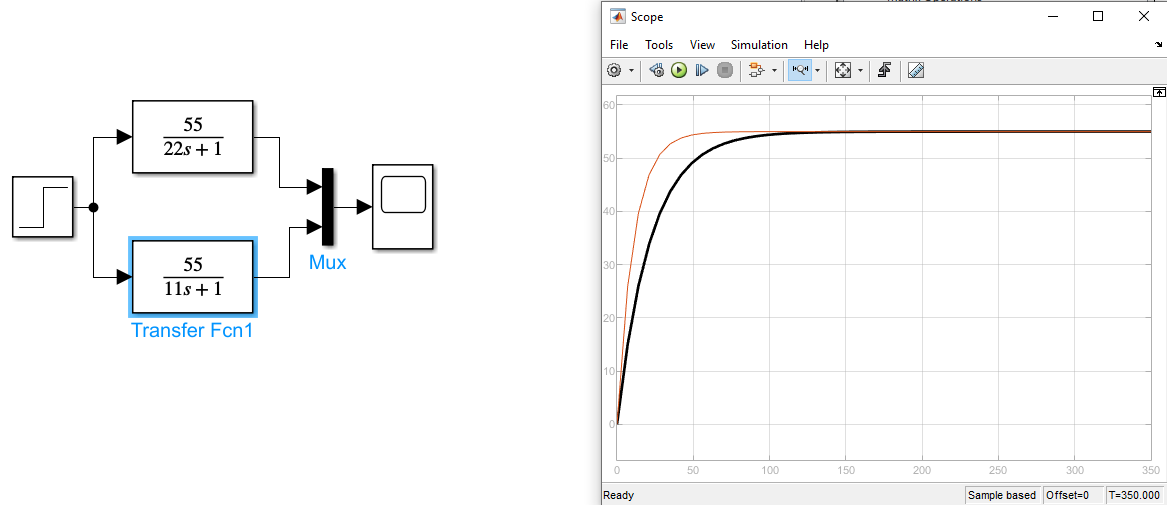
Рисунок 8 Графики передаточных функций апериодического звена с изменением постоянной времени
Красный график T1=11, черный – T2=22
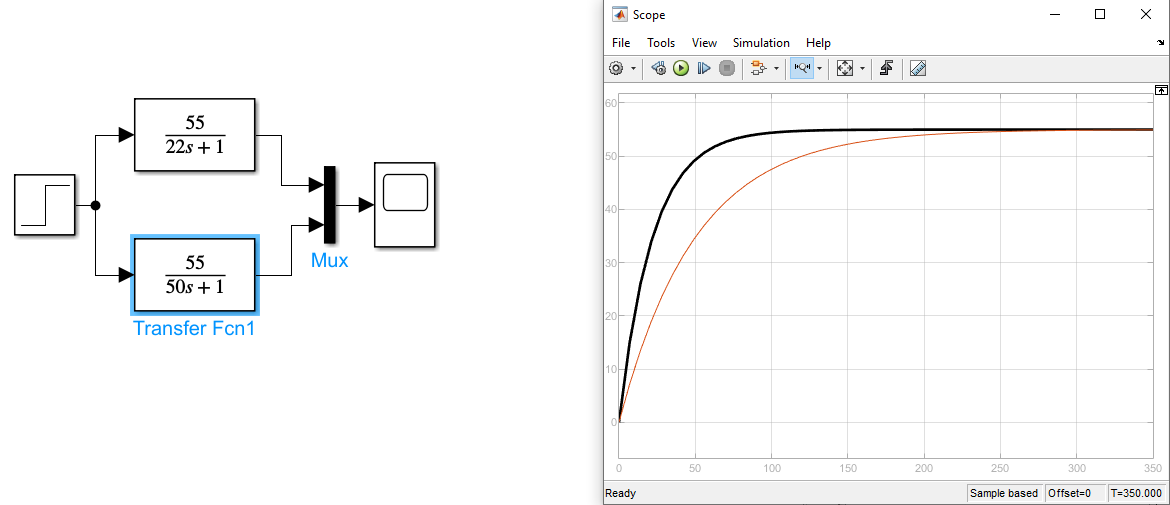
Рисунок 9 Графики передаточных функций апериодического звена с изменением постоянной времени
Красный график T1=50, черный T2=22
Задание 3
Создать график весовой характеристики
Её отличие в том что для нее нужен не ступенчатый входной сигнал, а импульсный который можно получить взяв производную от ступенчатого
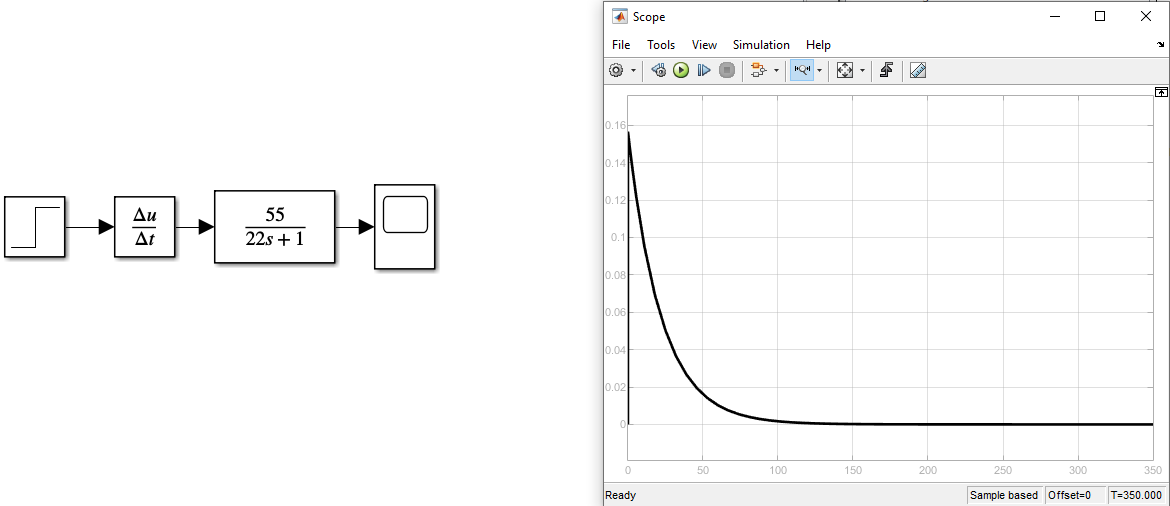
Рисунок 10 График весовой характеристики
Задание 4
Создать графики весовой характеристики с изменением данных
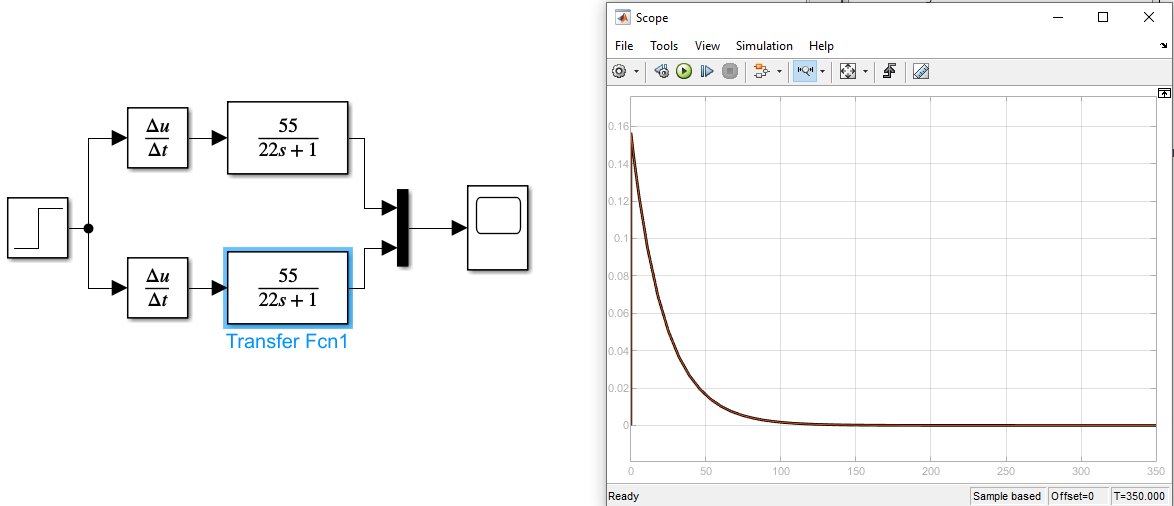
Рисунок 11 Графики весовой характеристики K1=K2=55 T1=T2=22
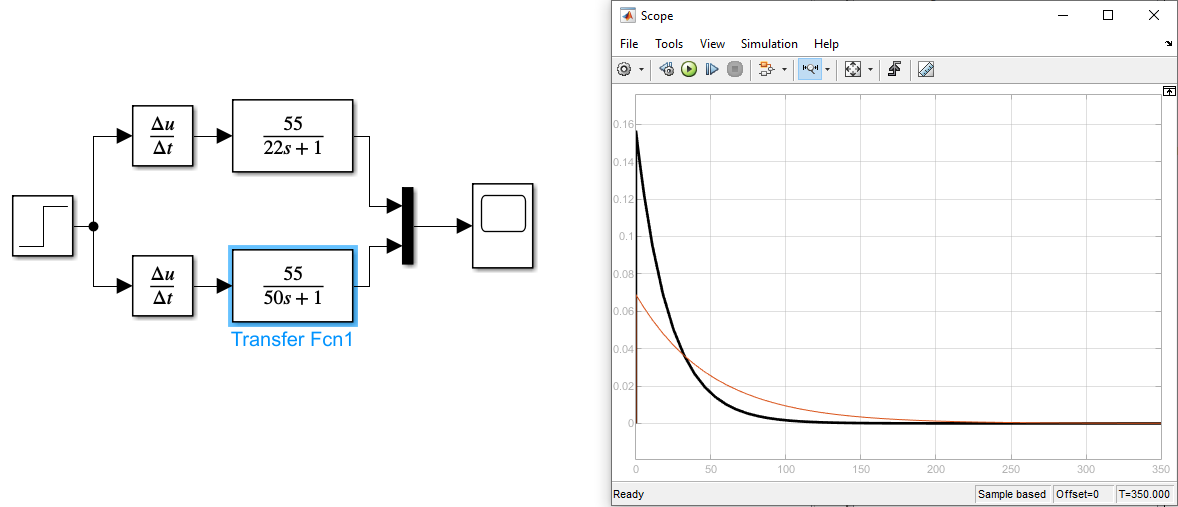
Рисунок 12 Графики весовой характеристики с изменением постоянной времени
Красный график T1=50, черный – T2=22
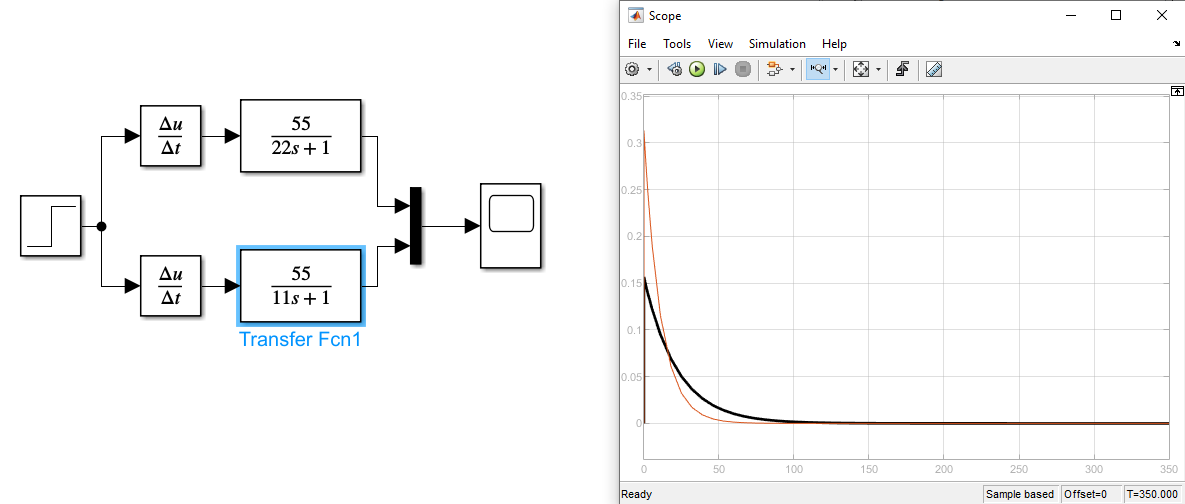
Рисунок 13 Графики весовой характеристики с изменением постоянной времени
Красный график T1=11, черный – T2=22
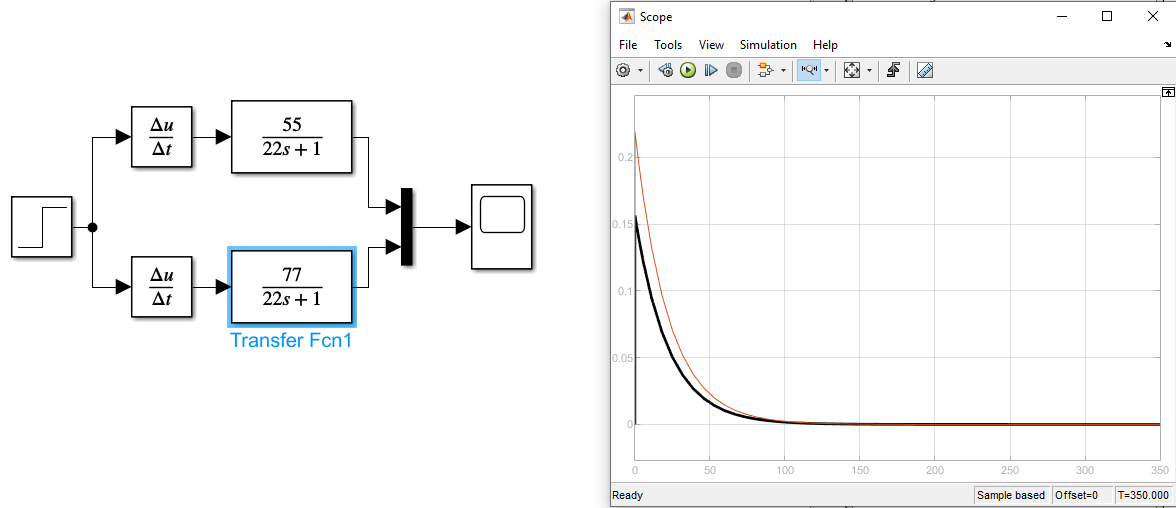
Рисунок 14 Графики весовой характеристики с изменением коэффициента усиления
Красный график K1=75, черный – K2=55
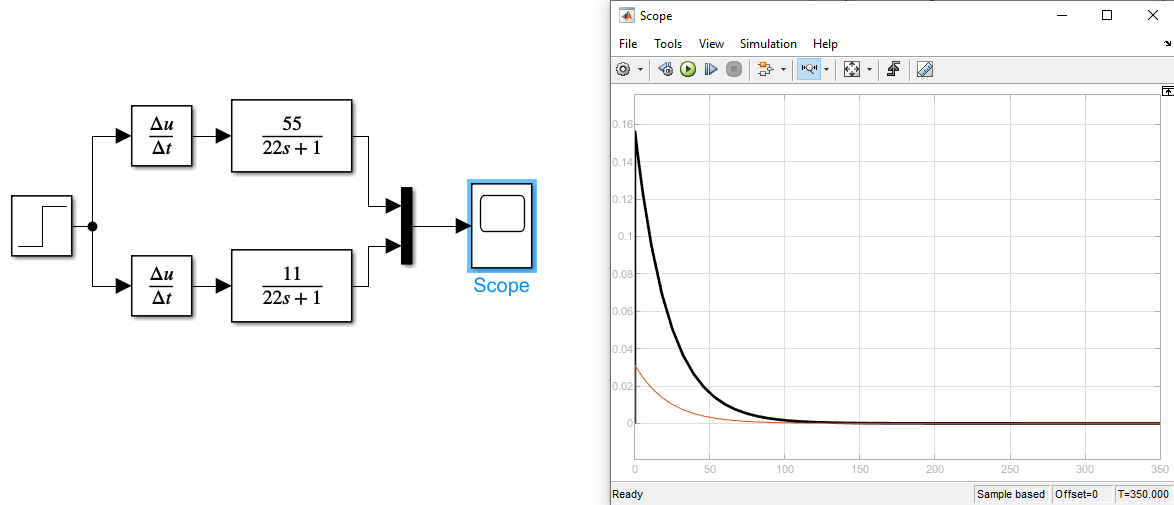
Рисунок 15 Графики весовой характеристики с изменением коэффициента усиления
Красный график K1=11, черный – K2=55
Задание 3
Создать график весовой ( импульсной ) функции колебательных звеньев
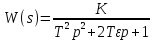
K- коэффициент усиления
T- постоянная времени
p- оператор Лапласа
 - коэффициент демпфирования
- коэффициент демпфирования 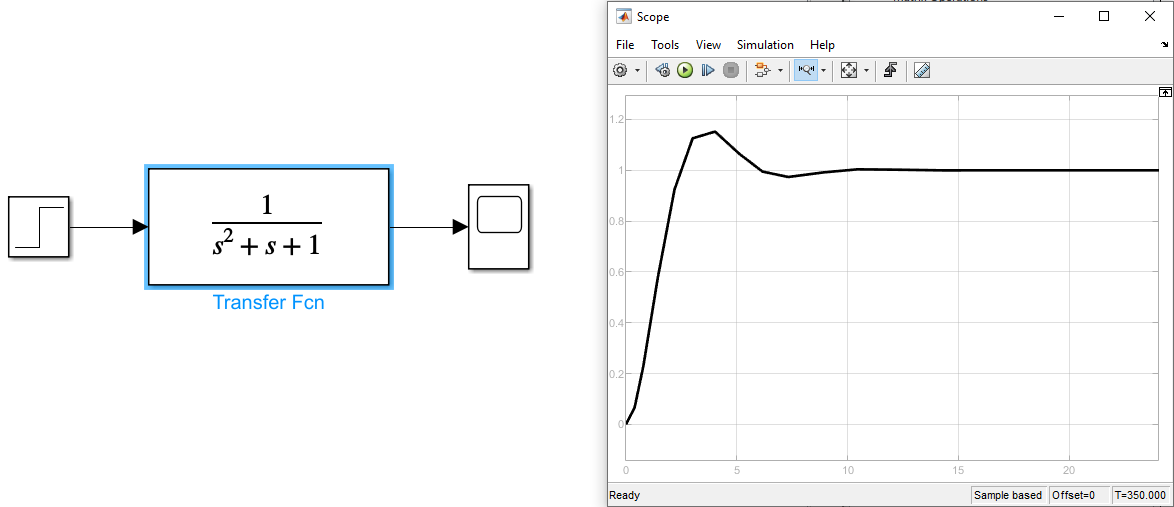
Рисунок 16 График весовой ( импульсной ) функции колебательных звеньев
Задание 5
Создать графики весовых ( импульсных ) функций колебательных звеньев с изменением данных
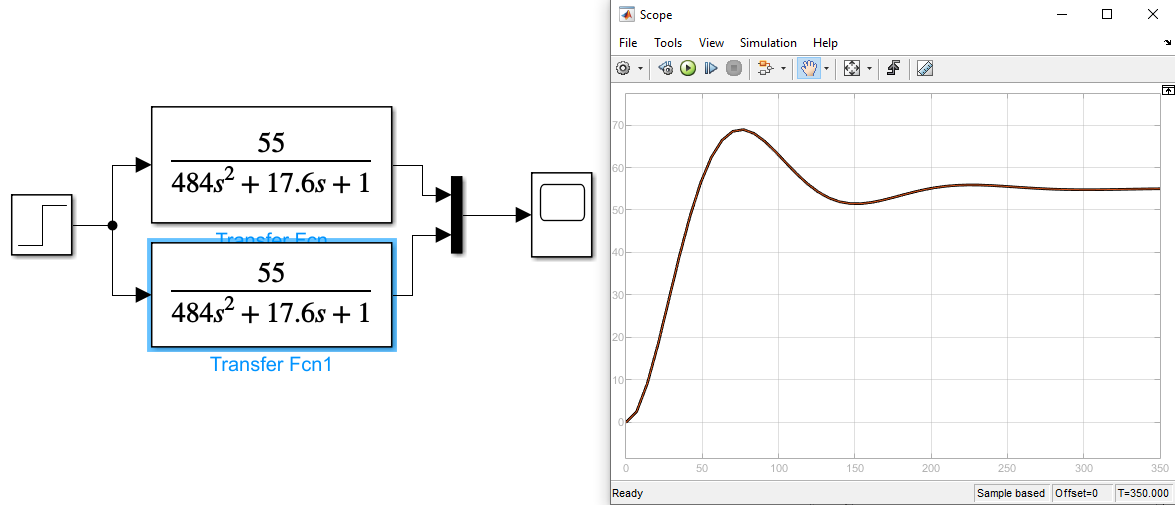
Рисунок 17 Графики весовых ( импульсных ) функций колебательных звеньев без изменений K=55, T=22, E=0.4
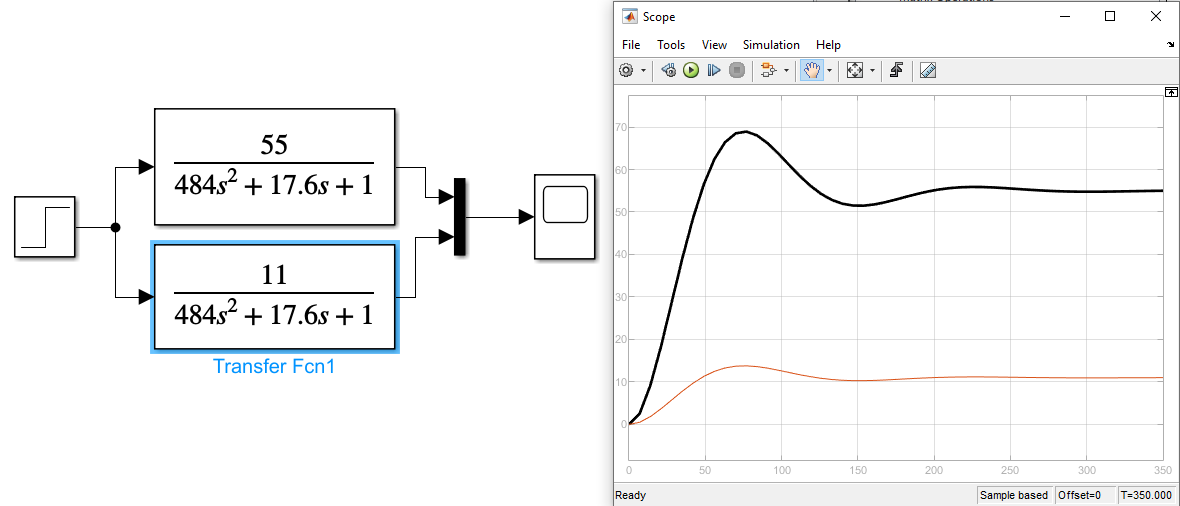
Рисунок 18 Графики весовых ( импульсных ) функций колебательных звеньев с изменением коэффициента усиления
Красный график K1=11, черный – K2=55
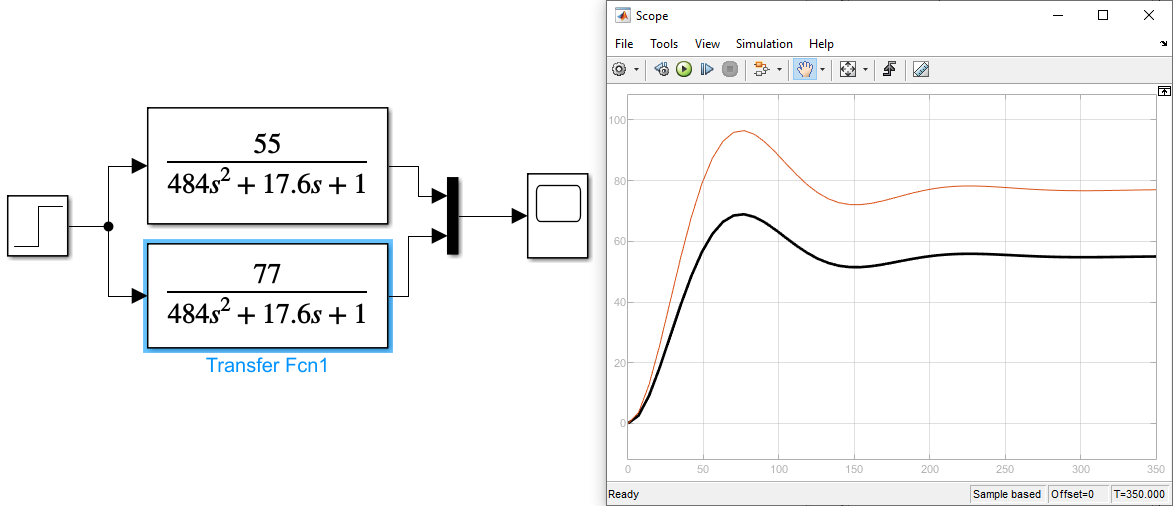
Рисунок 19 Графики весовых ( импульсных ) функций колебательных звеньев с изменением коэффициента усиления
Красный график K1=55, черный – K2=77
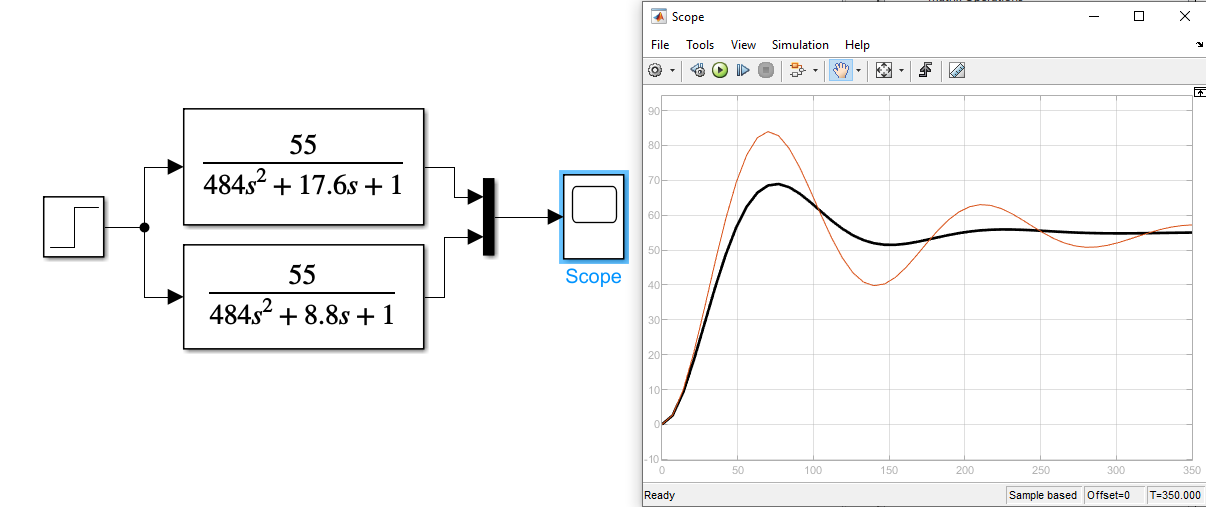
Рисунок 20 Графики весовых ( импульсных ) функций колебательных звеньев с изменением коэффициент демпфирования
Красный график
 1=0.2, черный –
1=0.2, черный –  2=0.4
2=0.4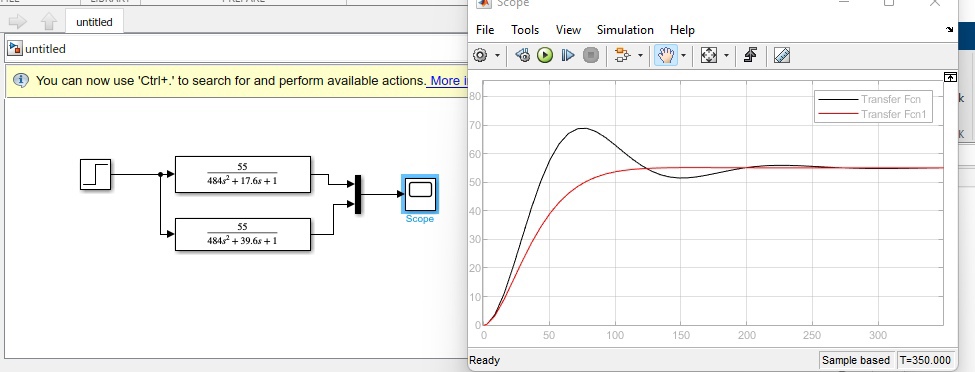
Рисунок 21 Графики весовых ( импульсных ) функций колебательных звеньев с изменением коэффициент демпфирования
Красный график
 1=0.9, черный –
1=0.9, черный –  2=0.4
2=0.4Вывод: Мы построили графики: придаточной функции апериодического звена, весовой характеристики, весовых ( импульсных ) функций колебательных, познакомились с интерфейсом и выполнили задания в программе Matlab.
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 2
Цель работы:
-
Ознакомиться с составом и назначением программной средой MATLAB и Simulink -
Ознакомиться с основными способами моделирования частотных характеристик объектов и систем управления
Задание
Создать блок схему позволяющую рассчитать АФХ, АЧХ, ФЧХ
Построим блок схему в программе Matlab позволяющую рассчитать АФХ, АЧХ, ФЧХ при K= 55, T=22.
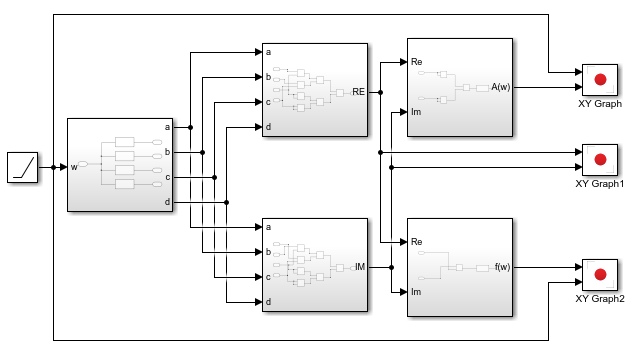
Рисунок 1-Блок схема позволяющая рассчитать АФХ, АЧХ, ФЧХ
Блок abcd предназначен для ввода в данных в формулу

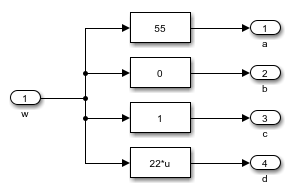
Рисунок 2-Блок abcd
Блок RE(W) предназначен для расчета действительной части алгебраической формы АФХ
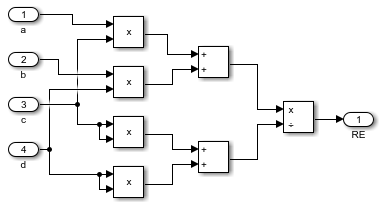
Рисунок 3-Блок RE(W)
Блок IM(W) предназначен для расчета мнимой части алгебраической формы АФХ
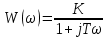
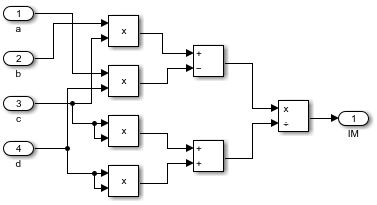
Рисунок 4-Блок IM(W)
Блок A(W) предназначен для расчета АЧХ


Рисунок 5-Блок A(W)
Блок F(W) предназначен для расчета ФЧХ
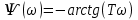

Рисунок 6-Блок F(W)
При запуске симуляции данной блок схемы мы получаем:
АФХ-амплитудно- фазовая характеристика
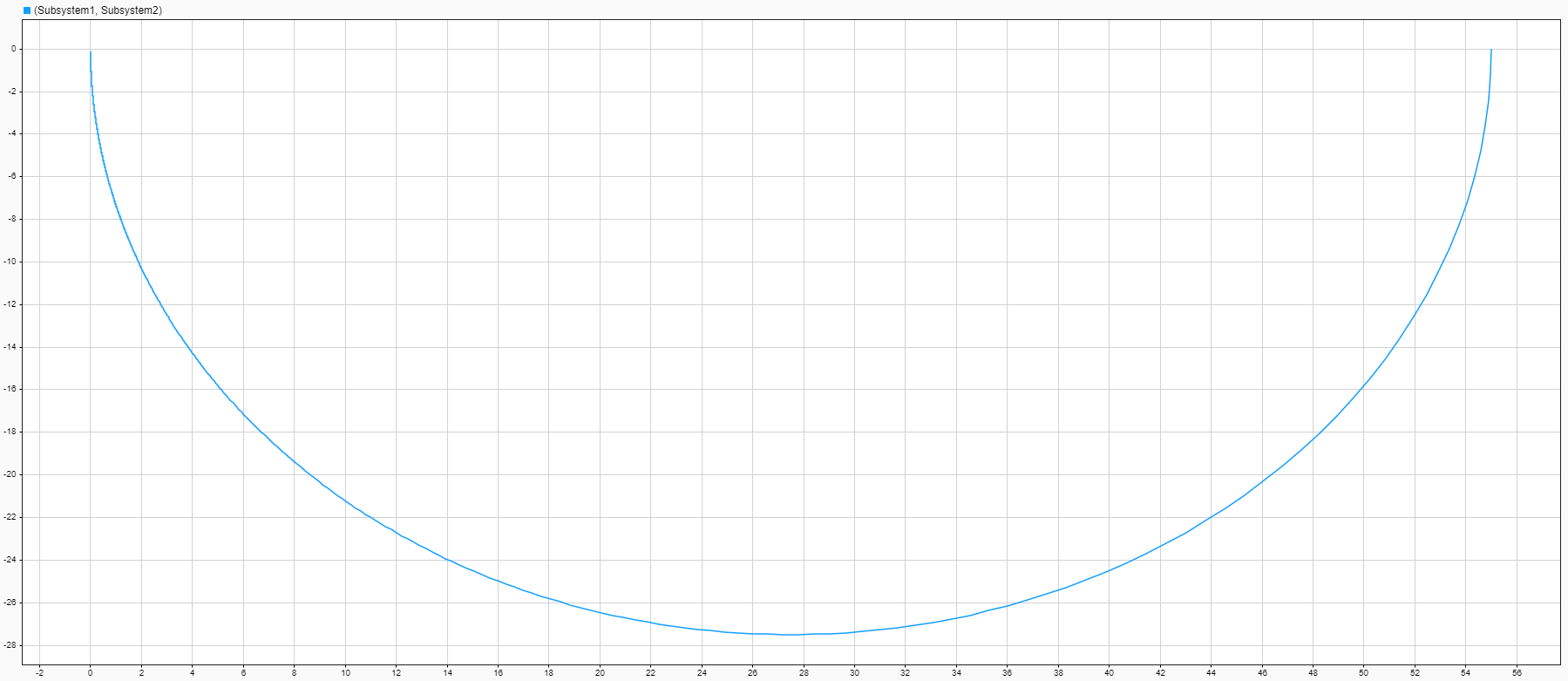
Рисунок 7-График амплитудно-фазовой характеристики (АФХ) при K= 55, T=22
АЧХ-амплитудно-частотная характеристика
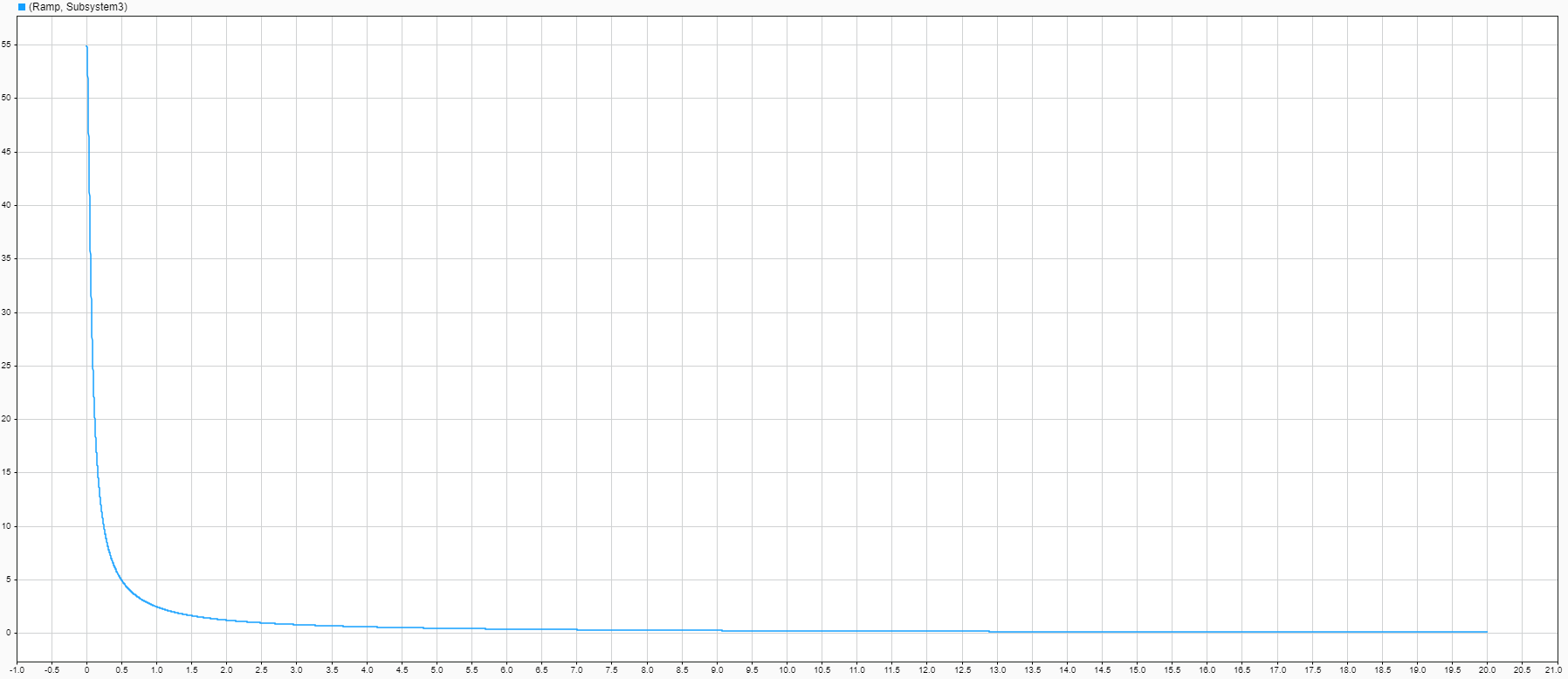
Рисунок 8-График амплитудно-частотной характеристики (АЧХ) при K= 55, T=22
ФЧХ-фаза-частотная характеристика(ФЧХ)
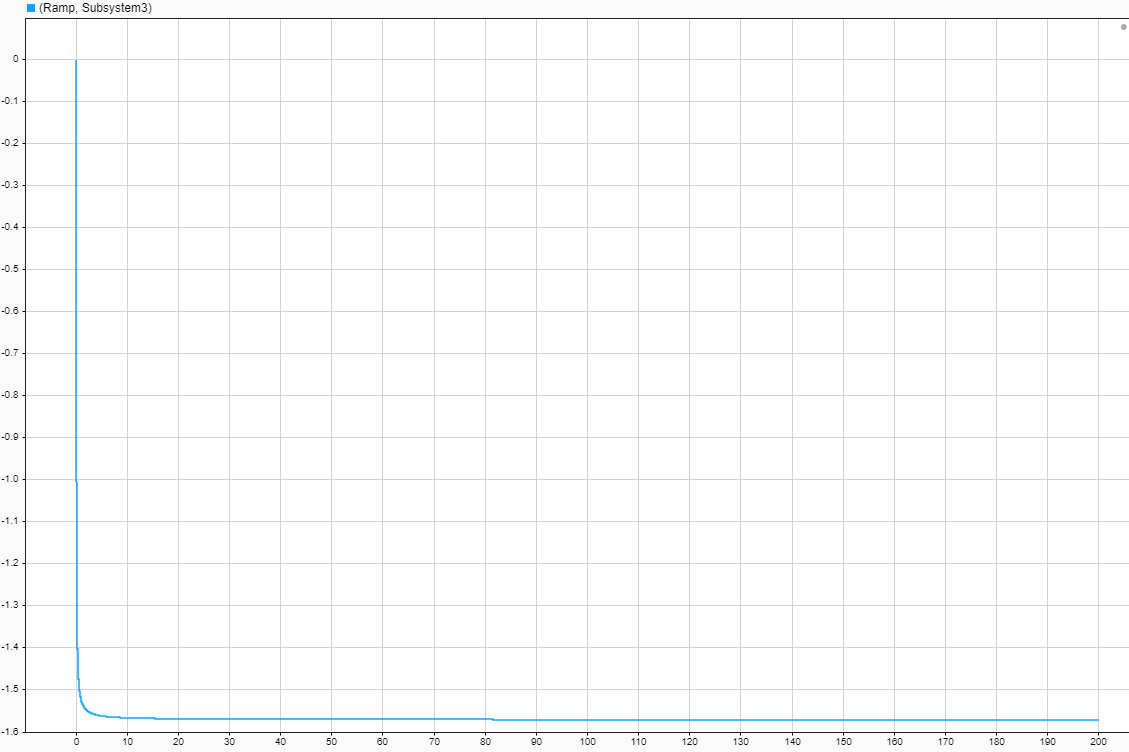
Рисунок 9-График фаза-частотной характеристики(ФЧХ) при K= 55, T=22
Вывод: в ходе работы было доказано, что частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Каждую функцию можно описать с помощью графиков, которые будут наглядно описывать воздействие на систему. Зная частотную характеристику элемента, можно определить реакцию элемента на гармоническое воздействие любой частоты, а также на сумму гармонических воздействий различной частоты.
Частотные характеристики широко используются в теории и практике автоматического управления, так как реальные возмущения, действующие на автоматические системы, могут быть представлены как сумма гармонических сигналов.
Программа MATLAB включает огромное количество способов моделирования частотных характеристик объектов и систем управления. Это помогает специалистом более точно определить различные воздействия, которые влияют на работу мехатронной системе и применять методы по их минимизации.
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 3
Цель работы: Исследование влияния параметров системы на устойчивость, определение критического передаточного коэффициента разомкнутой системы с использованием алгебраических критериев Гурвица и Гауса.