ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 9
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Теоретическое введение.
Ф
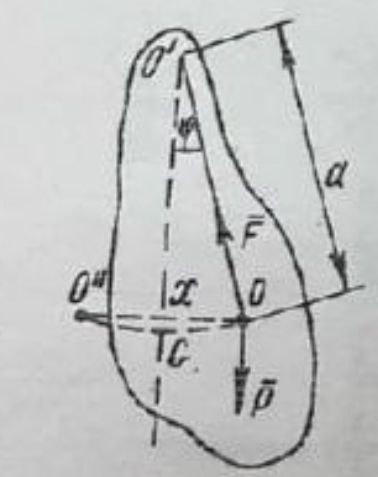изическим маятником называется тело, могущее совершать колебания около оси, смещенной относительно цента тяжести этого тела. На рисунке изображён схематический физический маятник, колеблющийся в поле тяжести около горизонтальной оси О’ перпендикулярной плоскости чертежа.
Если углы отклонения не превышает 5-6о, то маятник совершает гармонические колебания. Докажем это. Обратим внимание на то, что центр тяжести О маятника перемещается по дуге О”СО окружности радиуса ОО’, другие его точки – по дугам окружностей соответствующих радиусов. Имеет место вращательное движение относительно оси О’.
Внешнее воздействие на маятник определяется моментами сил F и P, причём векторы сил приложены к центру тяжести тела.
Результирующий момент этих сил равен:
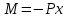. (1) Плечо для сил F равно нулю, поскольку линия действия силы пересекает ось О’. Плечо для силы Р обозначено х. Знак минус поставлен потому, что момент силы действует в направлении уменьшения х.
Вращающий момент М создаёт угловое ускорение ε. Запишем второй закон динамики для вращательного движения
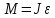(2)Здесь J – момент инерции физического маятника относительно оси вращения О’.
Угловым ускорение определяется:
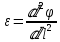(3)Объединим (3), (2) и (1). Получим:
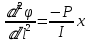(4)При углах отклонения до 60 справедливы соотношения:
; 
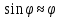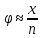(5)где а – расстояние от центра тяжести до оси вращения.
Дифференцируем (5) и подставляем в (4). Имеем:
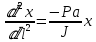(6)Решением дифференцированного уравнения (6) является:
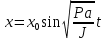(7)в чём можно убедится, если дифференцировать (7) дважды и поставить в (6).
Следовательно, при малых отклонениях физического маятника он совершает гармоническое (синусоидальное) колебания.
Определим период колебания физического маятника. Для этого напомним формулу смещения для синусоидальных колебаний:
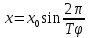(8)Сравнивая уравнения (8) с (7) получим:
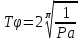(9)Или
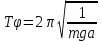(10)Уравнение (10) представляет собой формулу для периода колебания физического маятника. В нём m – масса физического маятника.
Математический маятник является частным случаем физического маятника, который представляет собой материальную точку, укрепленную на невесомой, нерастяжимой нити. Момент инерции точки массы m относительно оси О’:
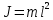(11)Вычислим период колебания математического маятника Тм. Для этого в (10) подставим (11). Имеем:
; 
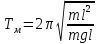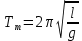. Сравнивая (12) с (10) даёт, если Тм = Тф:
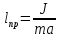. (13)Формула (13) определяет так так называемую приведенную длину физического маятника (lnp). Приведённой длинной физического маятника называется длина такого математического маятника, который имеет период колебания, равный с физическим.
-
Описание аппаратуры и метода измерений.
Физическим маятником млужит однородный металлический стержень. Он, опираясь с помощью муфты на призмы, может совершать колебания в плоскости, параллельной стене, относительно горизонтальной оси О’. Ось вращения совпадает с ребрами опорных призм.
Момент инерции J стержня (без учета муфты) относительно оси определим, исходя из теоремы Штейна:
J = J0 + ma2 (14)
где J0 – момент инерции стрежня относительно его центра тяжести: а – расстояние между осью вращения и центром тяжести, причем
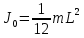(15)где
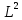
– длинна стержня.
Подставим (15) в (14), а (14) в (10). Получим, решая (10) относительно g:
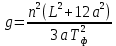(16)Измеряя период колебания физического маятника Тф, длину стержня L и удаление выреза муфты от центра стрежня a, можно вычислить по формуле (16) ускорение свободного падения g.
-
Обработка результатов измерения.
| | | Опыт 1 | |||
| | | a | n | t | T |
| № измерения | 1 | | | | |
| 2 | | | | ||
| 3 | | | | ||
| 4 | | | | ||
| 5 | | | | ||
| | | Опыт 2 | |||
| | | a | n | t | T |
| № измерения | 1 | | | | |
| 2 | | | | ||
| 3 | | | | ||
| 4 | | | | ||
| 5 | | | | ||
| | | Опыт 3 | |||
| | | a | n | t | T |
| № измерения | 1 | | | | |
| 2 | | | | ||
| 3 | | | | ||
| 4 | | | | ||
| 5 | | | | ||
| | G | ||
| | Опыт 1 | Опыт 2 | Опыт 3 |
| 1 | | | |
| 3 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
; 
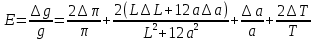
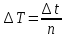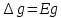
g =