Файл: Рубежный контроль к разделу Выберите правильный вариант ответа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 62
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рубежный контроль к разделу 1.
Выберите правильный вариант ответа
1. Предметом статистики как науки является...
A) метод статистики
Б) статистические показатели
B) количественные закономерности массовых варьирующих общественных
явлений
Г) группировки и классификации
2. Основным разделом статистической науки является
A) общая теория статистики
Б) промышленная статистика
B) теория вероятностей
Г) математическая статистика
3. Элементом какой отрасли статистической науки является статистика
строительства
A) экономическая статистика
Б) общей теории статистики
B) социальной статистики
Г) математической статистики
4. Вариация - это:
A) изменение состава совокупности
Б) изменение массовых явлений во времени
B) структуры статистической совокупности в пространстве
Г) изменение значений признака внутри наблюдаемой совокупности
5. Какие отчетные документы деятельности предприятия
представляются в органы государственной статистики?
A) декларация по страховым взносам на обязательное пенсионное
страхование
Б) расчетная ведомость по средствам фонда социального страхования
B) баланс и отчет о прибылях и убытках
Г) сведения о затратах на производство и продажу продукции
6. Статистический ряд распределения это.
A) бессистемное распределение единиц изучаемой совокупности
Б) распределение единиц изучаемой совокупности на группы по определенному
варьирующему признаку
B) хаотичное распределение единиц изучаемой совокупности
Г) упорядоченное распределение единиц изучаемой совокупности по баллам
7. Как называется ряд распределения, построенный по качественному
признаку?
A) дискретный
Б) атрибутивный
B) вариационный
Г) интервальный
8. В чем отличие дискретного ряда распределения от интервального?
А) варианты имеют значения целых чисел
Б) варианты имеют значения дробных чисел
В) варианты имеют значения отрицательных чисел
Г) варианты имеют значения комплексных чисел
9. Какие показатели не входят в состав обобщающих показателей?
A) абсолютные показатели
Б) относительные показатели
B) средние величины
Г) атрибутивные показатели
10. К какому классу относятся средняя арифметическая, средняя
гармоническая, средняя геометрическая?
A) к классу структурных средних
Б) к классу порядковых средних
B) к классу степенных средних
Г) к классу промежуточных средних.
11. Расположите средние величины в соответствии с правилом
мажорантности (в порядке возрастания).
A) средняя квадратическая, средняя арифметическая, средняя
геометрическая, средняя гармоническая
Б) средняя арифметическая, средняя геометрическая, средняя квадратическая,
средняя гармоническая
B) средняя гармоническая, средняя геометрическая, средняя
арифметическая, средняя квадратическая
Г) средняя геометрическая, средняя арифметическая, средняя квадратическая,
средняя гармоническая
12. Понятие средней величины.
A) обобщающий показатель, характеризующий структурные сдвиги
Б) частный показатель, характеризующий индекс цен
B) частный показатель, характеризующий развитие явления
Г) обобщающий показатель, характеризующий типичный уровень явления в
конкретных условиях места и времени
13. Основное условие правильного расчета средних величин.
A) рассчитываются для качественно однородных совокупностей
Б) рассчитываются для разнокачественных совокупностей
B) рассчитываются для качественно не однородных совокупностей
Г) рассчитываются для разнородных совокупностей по существенным
признакам
14. Какие два основных элемента имеется в таблице?
A) Подлежащее, сказуемое Б) Подлежащее, дополнение
B) Дополнение, обстоятельство Г) Сказуемое, обстоятельство
15. Какие существуют виды статистических таблиц?
А) Простые, групповые Б) Простые, сложные
В) Простые, групповые и комбинационные Г) Нет правильного варианта
16. Как называется график, созданный на основании накопленных
частот?
A) Гистограмма
Б) Полигон частот
B) Огива
Г) Линейная диаграмма
17. Что такое относительная величина в статистике?
A) Показатель, которым статистика характеризует совокупности единиц,
соединенных в группы или в целом
Б) Обобщающий показатель, который представляет собой частное от деления
двух статистических величин и характеризует количественное соотношение
между ними
B) Показатель, характеризующий уровень выполнения предприятием своих
обязательств, предусмотренных в договорах
Г) Показывает, насколько широко распространено изучаемое явление в той
или иной среде
18. В чем выражается относительная величина структуры?
A) В процентах, коэффициентах
Б) В коэффициентах, промилле
B) В промилле, процентах
Г) В децемилле, промилле
19. Что характеризуют относительные величины динамики?
A) характеризуют количественное соотношение одноименных показателей,
относящихся к различным объектам статистического наблюдения
Б) характеризуют соотношения между отдельными частями статистической
совокупности и показывают во сколько раз сравнимая часть совокупности
больше или меньше части, которая принимается за базу сравнения
B) характеризуют изменение изучаемого явления во времени, выявляют
направление развития, измеряют интенсивность развития
Г) характеризуют насколько широко распространено изучаемое явление в той
или иной среде
20. По какой формуле можно рассчитать относительную величину
структуры?
A) ОВd = Часть совокупности / Вся совокупность х 100%
Б) ОВd= ДО1 / ДО0 х 100%
B) ОВd = Часть совокупности / Вся совокупность
Г) ОВd= ДО1 / ДО0
Вариант №4.
1. Понятие, виды и задачи группировок.
Группировка – это разбиение совокупности на группы, однородные по какому – либо признаку.
Значение группировки состоит в том, что этот метод обеспечивает обобщение данных, представление их в обозримом виде; кроме того, группировка создает основу для последующей сводки и анализа данных.
С помощью метода группировок решаются следующие задачи:
- выделение социально – экономических типов явлений;
- изучение структуры явления и структурных сдвигов, происходящих в нем;
- выявление связи и зависимости между явлениями.
В соответствии с задачами группировки различают следующие её виды: типологическая, структурная, аналитическая.
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов путем разделения качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки. Примерами типологической группировки могут служить группировки по секторам экономики, предприятий по формам собственности.
Структурной называется группировка, в которой происходит разделение однородных совокупностей на группы; характеризующие их структуру по какому-либо варьирующему признаку. Эта группировка дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. К ним относится группировка по населения по полу, возрасту, по размеру среднедушевого дохода, группировка хозяйств по объёму продукции.
Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой. Например, группировка предприятий определенной отрасли экономики по уровню производительности труда для выявления её влияния на себестоимость продукции.
В зависимости от степени сложности массового явления группировки могут производиться по одному или нескольким признакам.
Группировка по двум или нескольким признакам называется сложной (многомерной). Частным случаем многомерной группировки является комбинационная группировка. Если группы, образованные по одному признаку, делятся затем на подгруппы по второму и т. д. признакам, т. е. в основании группировки лежит несколько признаков, взятых в комбинации, то такая группировка называется комбинационная.
В зависимости от вида группировочных признаков различают группировки по атрибутивным и количественным признакам.
По отношению между признаками выделяют иерархические и неиерархические группировки.
Иерархические группировки выполняются по двум и более признакам, при этом значения второго признака определяется областью значения первого.
Неиерархические группировки строятся, когда строгой зависимости значений второго признака от первого не существует.
Относительно временного критерия группировки бывают статические и динамические. Динамические – это группировки, показывающие переходы единиц из одних групп в другие.
По очередности обработки информации группировки бывают первичные и вторичные, являющиеся результатом перегруппировки. Применяются два способа образования новых групп: 1) изменение (чаще укрупнение) первоначальных интервалов; 2) долевая перегруппировка – образование новых групп на основе закрепления за каждой группой определенной доли единиц совокупности.
2. Мода и техника её исчисления.
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
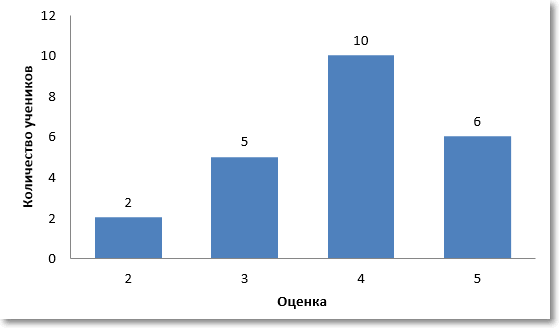
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
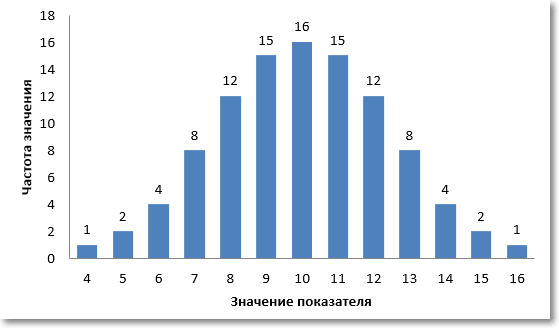
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
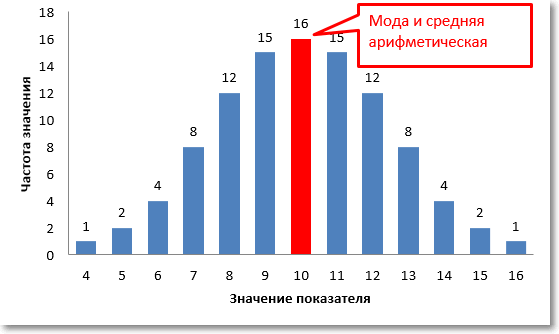
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
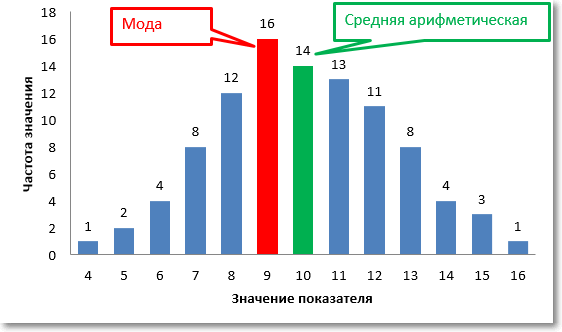
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.