Файл: Рубежный контроль к разделу Выберите правильный вариант ответа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 63
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
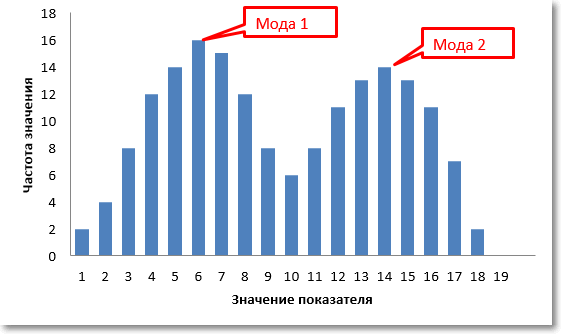
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
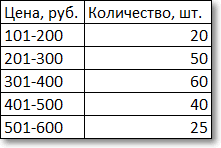
Для наглядности изобразим соответствующую диаграмму.
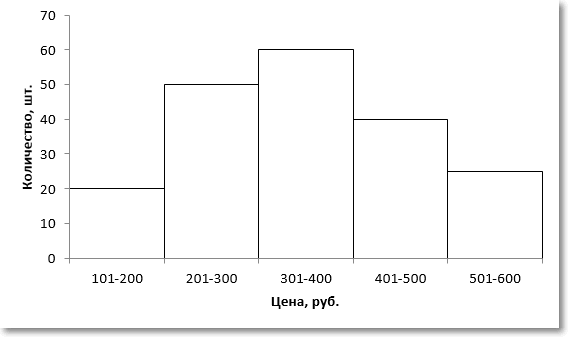
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
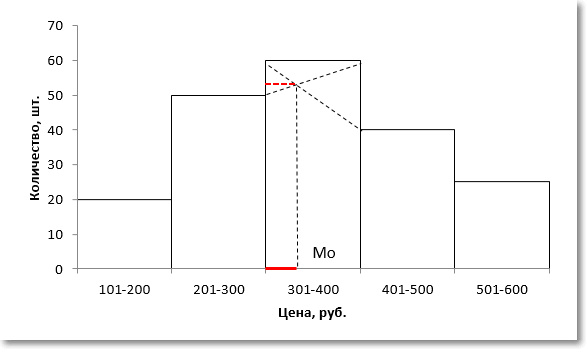
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
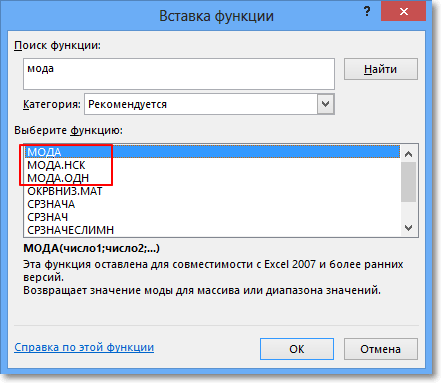
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
3. Статистические графики и их виды.
Статистический график – это чертёж, на котором статистические совокупности, характеризуемые определёнными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблиц в виде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковывать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. График должен быть выразительным, доходчивым и понятным, включать ряд основных элементов – графический образ, поле графика, пространственные ориентиры, масштабные ориентиры, экспликацию графика.
Графический образ (основа графика) – это геометрические знаки, т. е. совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели. Важно правильно выбрать графический образ, который должен соответствовать цели графика и способствовать наибольшей выразительности изображаемых статистических данных. Графическими являются лишь те образы, в которых свойства геометрических знаков – фигура, размер линий, расположение частей – имеют существенное значение для выражения содержания изображаемых статистических величин, причём каждому изменению выражаемого содержания соответствует изменение графического образа.
Поле графика – это часть плоскости, где расположены графические образы. Поле графика характеризуется его форматом (размерами и пропорциями сторон). Размер поля графика зависит от его назначения. Стороны поля графика обычно находятся в определённой пропорции. Принято считать, что наиболее оптимальным для зрительного восприятия является график, выполненный на поле прямоугольной формы с соотношением сторон от 1 : 1,3 до 1 : 1,5 (правило «золотого сечения»). Иногда используется и поле графика с равными сторонами, т. е. имеющее форму квадрата.
Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее распространённой является система прямоугольных координат.
Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика – это мера перевода числовой величины в графическую. Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определённые числа. Шкала имеет большое значение и включает три элемента: линию (или носитель шкалы), определённое число помеченных черточками точек, которые расположены на носителе шкалы в определённом порядке, цифровое обозначение чисел, соответствующих отдельным помеченным точкам.
Последний элемент графика – экспликация. Каждый график должен иметь словесное описание. Оно включает его содержание, подписи вдоль масштабных шкал и пояснения к отдельным частям графика.
По форме графического образа статистические графики бывают:
· линейные (статистические кривые);
· плоскостные (столбиковые, полосовые, квадратные, круговые, секторные, фигурные, точечные, фоновые);
· объёмные (поверхностные распределения).
По способу построения статистические графики делятся на диаграммы и статистические карты. Диаграммы – наиболее распространённый способ графических изображений. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.), независимых друг от друга величин: территорий, населения т. д. В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные диаграммы и диаграммы динамики. Статистические карты – графики количественного распределения по территории. По своей цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространённость статистических данных. Статистические карты по графическому образу делятся на картограммы и картодиаграммы
Наиболее распространёнными диаграммами сравнения являются столбиковые диаграммы, принцип построения которых состоит в изображении статистических показателей в виде поставленных по вертикали прямоугольников – столбиков. Каждый столбик изображает величину отдельного уровня исследуемого статистического ряда. Таким образом, сравнение статистических показателей возможно потому, что все сравнимые показатели выражены в одной единице измерения.
Разновидностью столбиковых диаграмм являются ленточные или полосовые диаграммы. В ленточных диаграммах основания столбиков располагаются вертикально, а масштабная шкала наносится на горизонтальную ось.
Квадратные и круговые диаграммы относятся к типу плоскостных диаграмм. Они представляют собой различные по размеру квадраты или круги, площади которых пропорциональны величине изображаемых статистических данных. Недостаток этих диаграмм в том, что они менее наглядны, чем столбиковые, т. к. сравниваются площади, а не высоты и строить их несколько сложнее.
Наиболее распространённым способом графического изображения структуры статистических совокупностей является секторная диаграмма, которая считается основной формой диаграммы такого назначения. Структура того или иного явления изображается с помощью кругов, разделённых на секторы, пропорциональные долям частей явлений. Круг принимается за целое (100 %) и разбивается на секторы, дуги которых пропорциональны значениям отдельных частей отражаемых величин. Дуга каждого сектора рассчитывается по формуле: , где - площадь круга (100 %), а d – величина изображаемого явления в процентах. Секторные диаграммы следует применять лишь в тех случаях, когда совокупность делится не более, чем на 4 – 5 частей, а также при условии значительных различий сравниваемых структур. В противном случае они теряют свою выразительность.
Для изображения развития явления во времени строятся диаграммы динамики. Для наглядного изображения явлений в рядах динамики используются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. выбор вида диаграммы зависит в основном от особенностей исходных данных, цели исследования. Когда число уровней в ряду динамики велико, целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать: в том случае, если целью исследования является изображение общей тенденции и характера развития явления или когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения.
4. Задача. По плану на 2020 год предполагалось увеличить производство
продукции с 5650 шт. до 6100 шт. В действительности в 2020 году было
произведено продукции 5850 шт. Найти относительные величины планового задания, выполнения планового задания.
Решение:
ОПП = 6100 / 5650 = 1,08
т.е. по плану предполагалось увеличить производство продукции в 1,08 раза,
это - плановый коэффициент роста (плановый индекс роста).