5. Спектр интеграла от сигнала:
s(t)↔ S( )

______________________ (3.5)



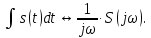
Вывод: спектр сигнала, равного интегралу от исходного сигнала, равен спектру исходного сигнала, деленному на . При этом амплитудный спектр изменяется обратно пропорционально изменению частоты , т.е. амплитудный спектр равен S( )/ , а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная -π/2.

6. Спектр радиоимпульса:
s_в(t)↔ S_в( )

___________________________________________ (3.6)

s_в(t)cos 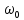t↔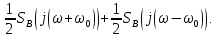

Вывод: обратим внимание, что спектр видеоимпульса отображается в области низких частот – низкочастотный сигнал, а спектр радиоимпульса – высоких частот – высокочастотный сигнал.

7. Спектр произведения двух сигналов:
s₁(t)↔ S₁( )

s₂(t)↔ S₂( )

_____________________________ (3.7)

s₁(t)s₂(t)↔

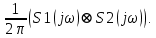
Вывод: Спектр произведения двух сигналов равен свертке их спектров, умноженной на коэффициент 1/(2π).
В данном разделе мы рассмотрели свойства преобразования Фурье. Данные свойства в дальнейшем будут использоваться для расчета спектральных характеристик сигнала 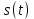, заданным в курсовом проекте.

---

4 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ОДИНОЧНОГО ВИДЕОИМПУЛЬСА
Сигналы, используемые в радиотехнике, имеют достаточно сложную структуру. Математическое описание таких сигналов является трудной задачей. Поэтому для упрощения процедуры анализа сигналов и прохождения их через радиотехнические цепи используют прием, предусматривающий разложение сложных сигналов на совокупность идеализированных математических моделей, описываемых элементарными функциями.

В радиотехнике в качестве непериодических сигналов рассматривают обычно одиночные импульсные сигналы. Для спектрального анализа таких сигналов используются  преобразования  Фурье  [1]:

; (4.1)

Из условия нам известно:

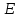=6 В; 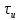=50 мкс, где 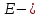амплитуда сигнала; 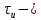длительность импульса.

В соответствии с заданием курсовой работы необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 4.1.



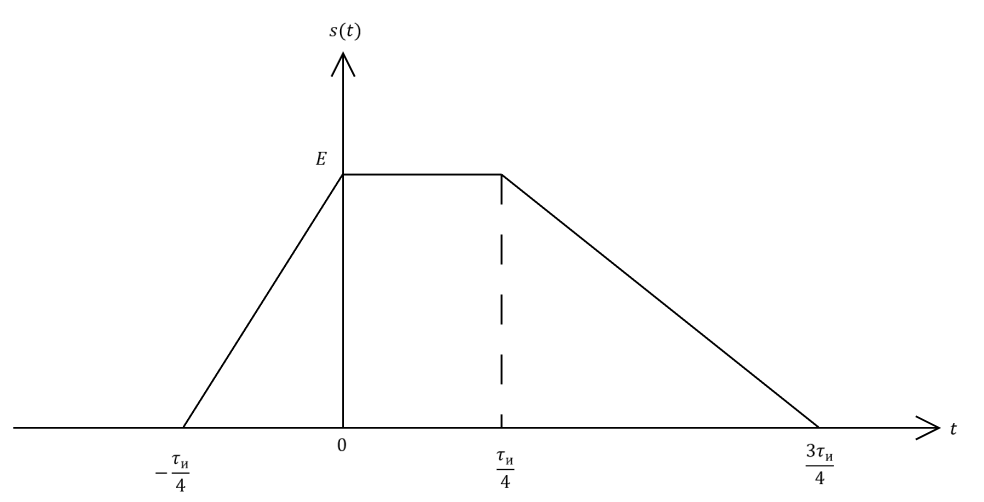
Рисунок 4.1– Одиночный видеоимпульс

Форма сигнала заданного в курсовом проекте имеет вид:


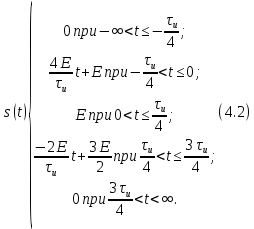
Так как форма сигнала является произвольной , то наш сигнал имеет действительную и мнимую часть, поэтому для расчёта спектра сигнала мы используем прямое преобразование Фурье:
.
Подставим формулу сигнала, зная ,что при
;

---

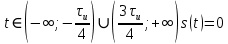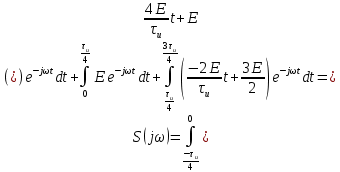
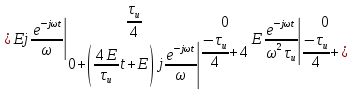
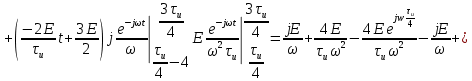
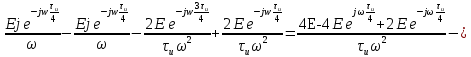
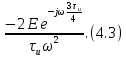
Для того, чтобы отделить мнимую часть от действительной воспользуемся формулами Эйлера, которые представлены ниже:












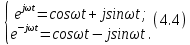
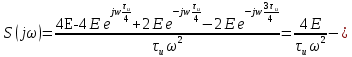
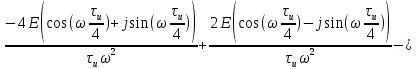
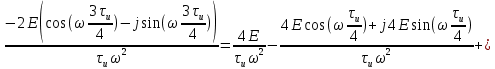
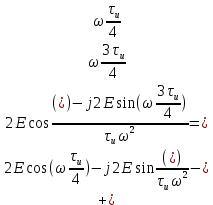
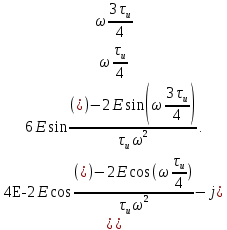
Так как:
,
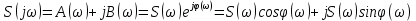  где 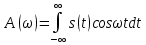– действительная часть спектра;
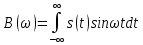– мнимая часть спектра;
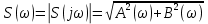– амплитудный спектр сигнала;
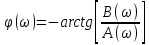– фазовый спектр сигнала.
Получим:



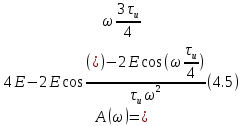
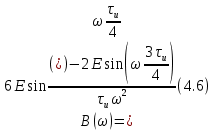
Амплитудный спектр [1]:

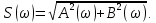
Фазовый спектр[1]:


Следовательно:



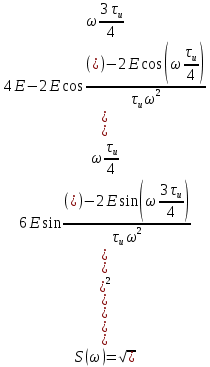
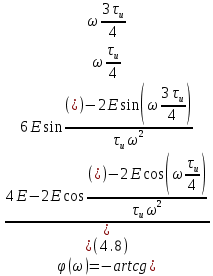
Перейдем от к 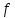,применим это к формулам (4.7),(4.8):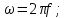





Следовательно:




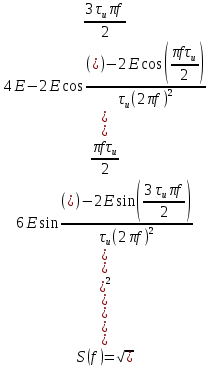
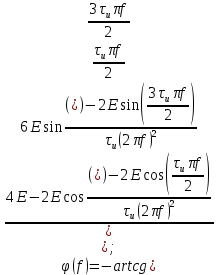
Подставив численные значения получим:

---

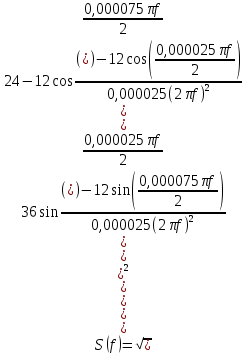
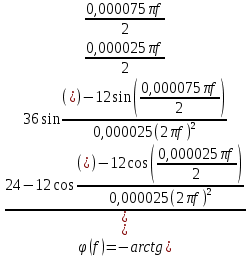
По полученной формуле построим график амплитудного спектра:



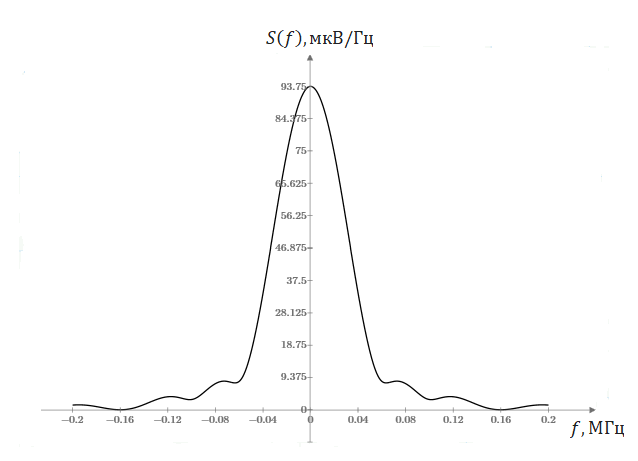
Рисунок 4.2 – Амплитудный спектр одиночного видеоимпульса
В данном разделе были рассчитаны амплитудный и фазовый спектры одиночного видеоимпульса. Был построен график амплитудного спектра (рисунок 4.2) одиночного видеоимпульса (рисунок 4.1). Для расчёта использовались: прямое преобразование Фурье, свойство четных сигналов и формулы Эйлера.

5 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ВИДЕОИМПУЛЬСОВ
В соответствии с заданием на курсовую работу необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 5.1 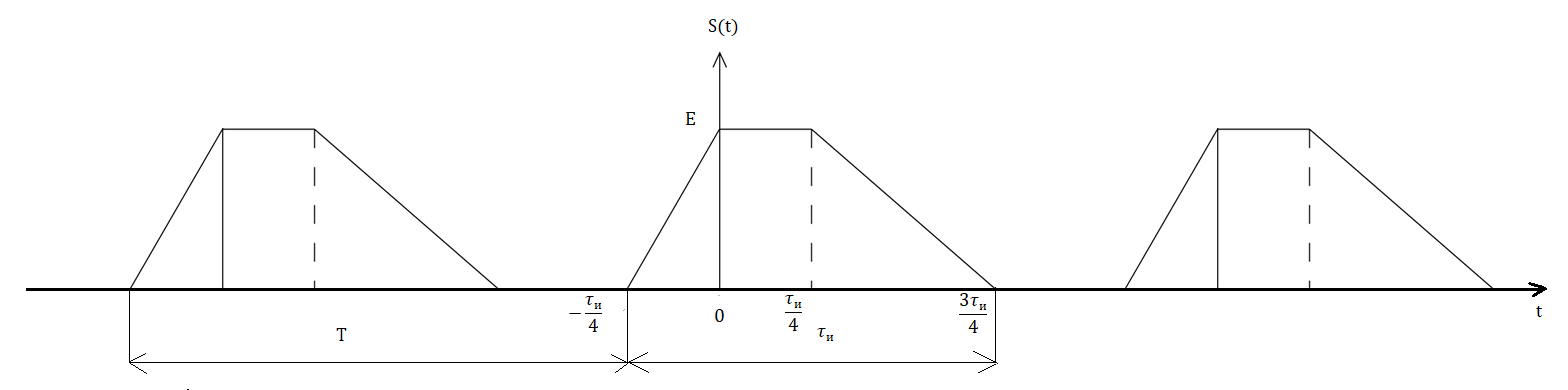Рисунок 5.1 – Периодическая последовательность видеоимпульсов Исходные данные: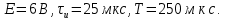

Как видно из рисунка 3.1 сигнал является периодическим, поэтому для определения его спектральных характеристик необходимо использовать комплексную форму ряда Фурье[2]:
Определим


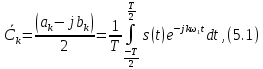
где: s(t) – сигнал, 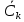– спектр к-той гармоники, k=1, 2, 3, ….

– угловая частота, рад/с.
Подставим формулу данного сигнала:




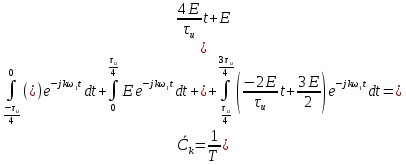
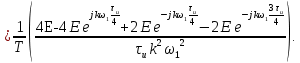
Для того, чтобы отделить мнимую часть от действительной воспользуемся формулами Эйлера, которые представлены ниже:

---

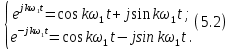
Следовательно:



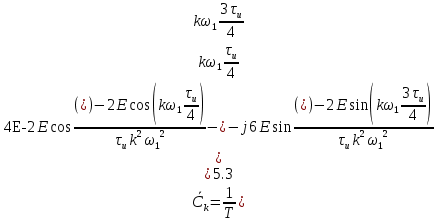
Примем:

Действительная часть спектра:


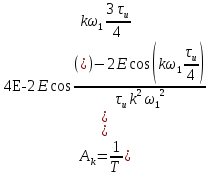
Мнимая часть спектра:


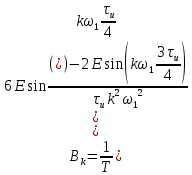
Амплитудный спектр:


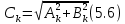
Фазовый спектр:



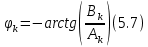
Следовательно:



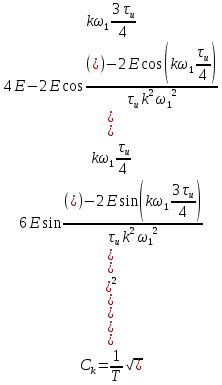
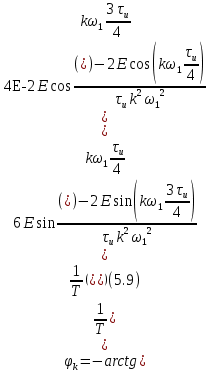
Найдём 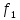как: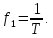


Перейдём от к :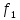






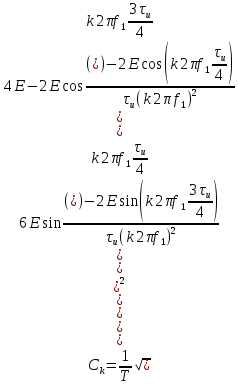
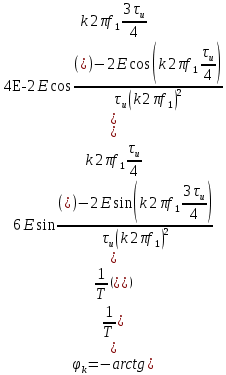
Перейдём от 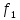к T: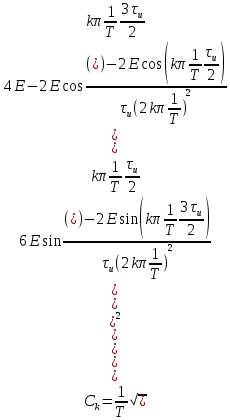



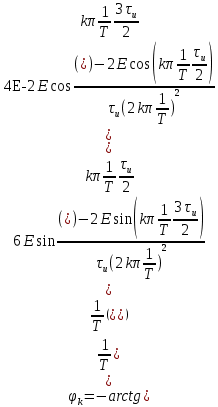
Подставим численные значения:




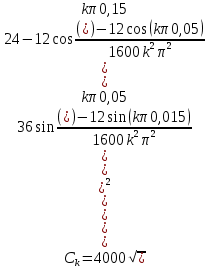
Подставим численные значения:



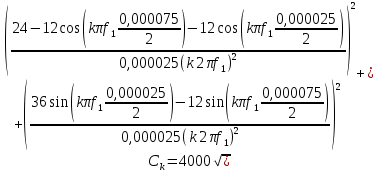
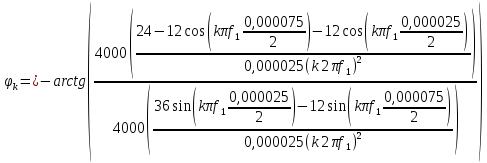
В соответствии с полученной формулой построим график амплитудного спектра:

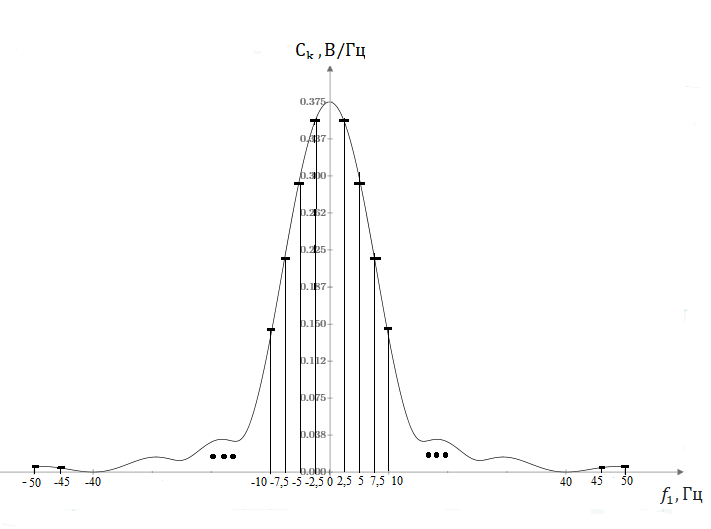
Рисунок 5.2 – Амплитудный спектр периодической последовательности видеоимпульсов
В данном разделе были рассчитаны амплитудный и фазовый спектры периодической последовательности видеоимпульсов. Был построен график амплитудного спектра (рисунок 5.2) периодической последовательности радиоимпульсов (рисунок 5.1). Для расчёта использовались: ряд Фурье в комплексной форме, свойство четных сигналов и формулы Эйлера.

---

Смотрите также файлы

• Основные черты налогового контроля в рф.docx

• Трбиені масаты мен міндеттері. Трбие.docx

• Практическая работа к теме Доверие к государству Тема занятия Наша страна россия. Класс 5.docx

• В качестве файлового сервера организации выступает сервер.docx

• О вере, неверии и сомнении Часть I. Детская вера Часть ii. Разумная вера.pdf