6 РАСЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ОДИНОЧНОГО РАДИОИМПУЛЬСА
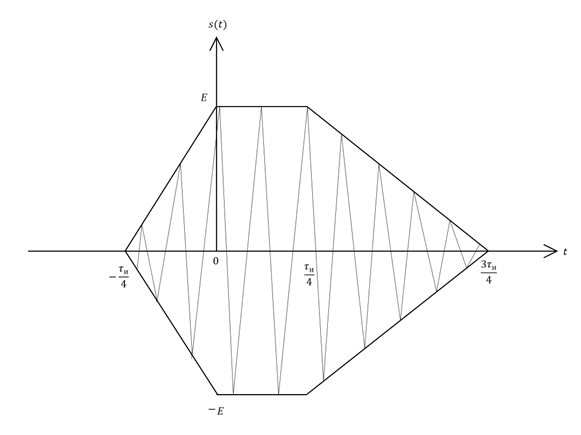
В соответствии с заданием на курсовую работу необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 6.1.


Исходные данные:

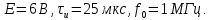
Как видно из рисунка 6.1, сигнал является одиночным радиоимпульсом, т.е. непериодическим сигналом. Для определения спектра этого сигнала используем одно из свойств преобразований Фурье, а именно смещением спектра сигнала.

Для упрощения расчёта спектра данного сигнала воспользуемся формулой преобразования Фурье [4] и формулой 2.1



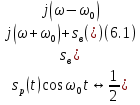
Тогда получим:



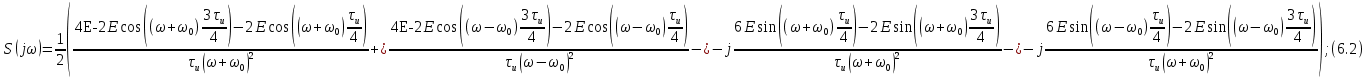
– амплитудный спектр сигнала,

где –действительная часть спектра;

– мнимая часть спектра.

Cледовательно:







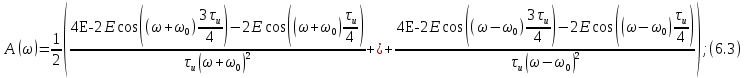
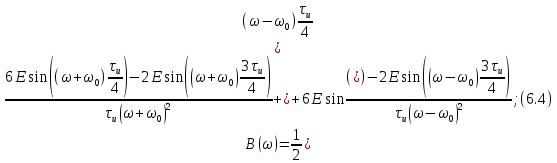
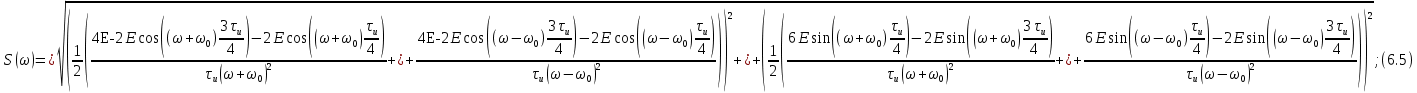
Сделаем переход



    

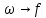
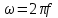
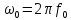
Тогда получим:



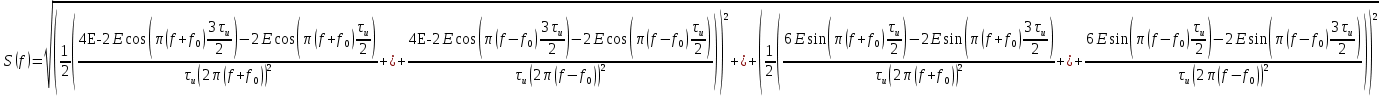
Подставим численные значения:

;

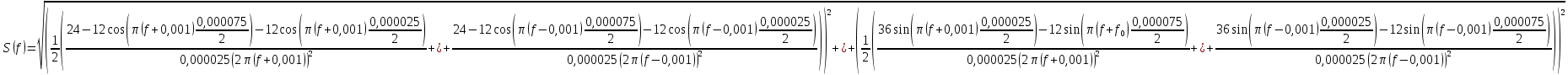Фазовый спектр одиночного радиоимпульса:



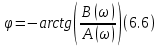
Тогда:

;

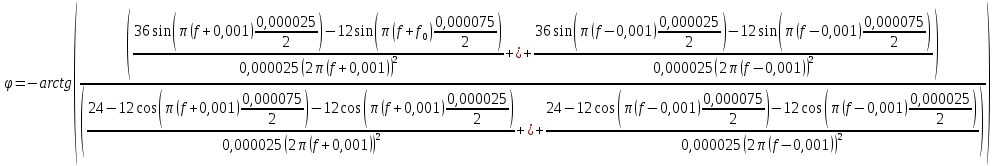По полученной формуле построим график амплитудного спектра:


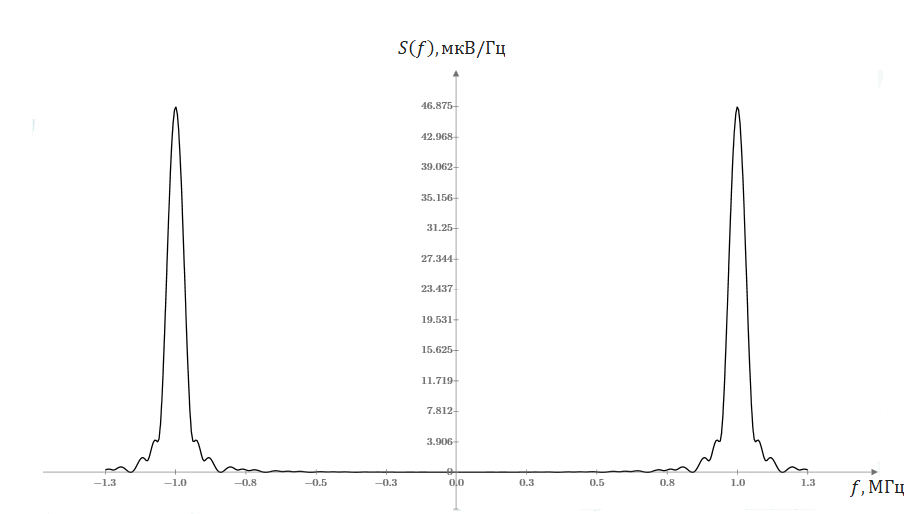
Рисунок 6.2 – Амплитудный спектр одиночного радиоимпульса

В данном разделе были рассчитаны амплитудный и фазовый спектры одиночного радиоимпульса. Был построен график амплитудного спектра (рисунок 6.2) одиночного радиоимпульса (рисунок 6.1). Для расчёта использовались свойства преобразования Фурье.

---

7 РАСЧЁТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК

     ПЕРИОДИЧЕСКИХ РАДИОИМПУЛЬСОВ

В соответствии с заданием на курсовую работу необходимо рассчитать амплитудный и фазовый спектры сигнала, представленного на рисунке 7.1

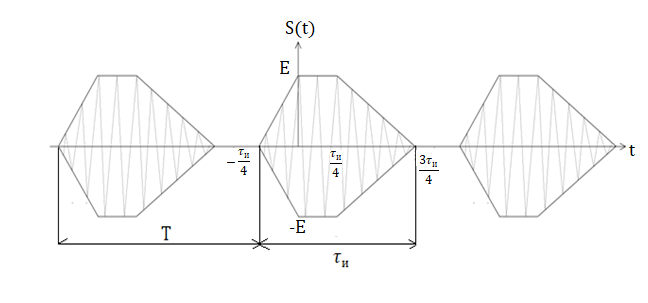
Рисунок 7.1 – Периодическая последовательность радиоимпульсов

Исходные данные:

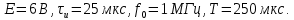
Как видно из рисунка 7.1 сигнал является периодическим, поэтому для определения его спектральных характеристик необходимо использовать свойства преобразования Фурье опираясь на спектральную плотность периодической последовательности видеоимпульсов:


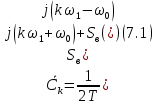
Следовательно, в нашем случае получим, что:

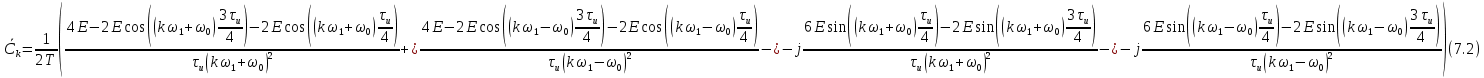
Примем:

Действительная часть спектра:

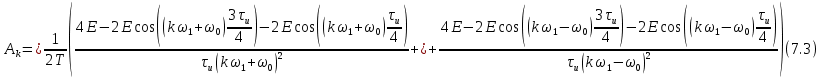
Мнимая часть спектра:


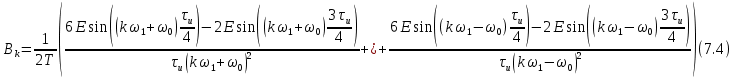
Амплитудный спектр:

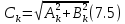
Фазовый спектр:

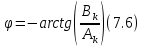
Подставим:




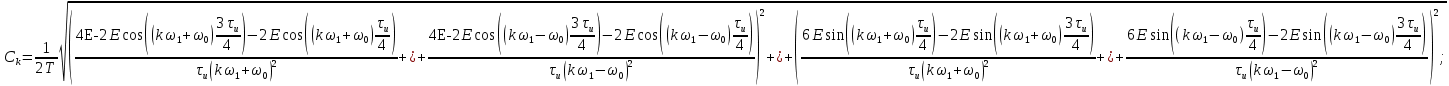
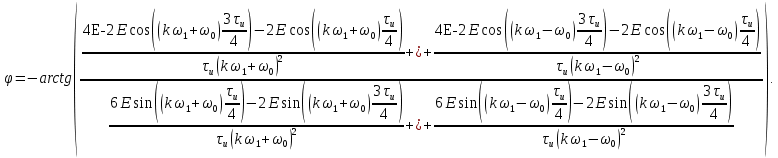
Перейдём от к использую следующие формулы: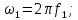








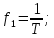
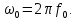
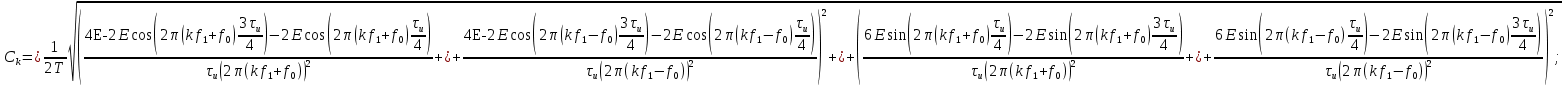
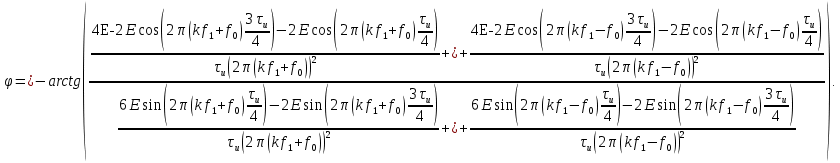
Подставим числовые значения:

.

---

.
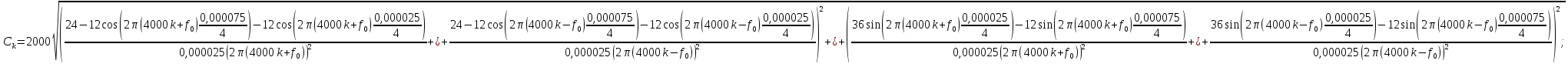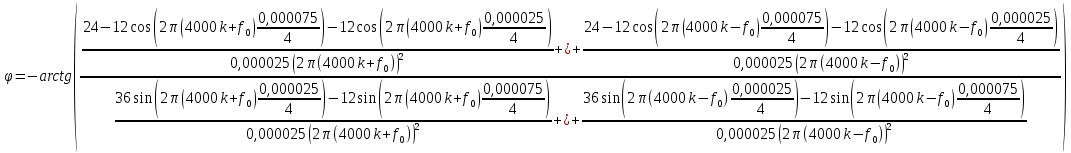
Построим график :

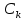Рисунок 7.2 – Амплитудный спектр периодической последовательности радиоимпульсов

В данном разделе были рассчитаны амплитудный и фазовый спектры периодической последовательности радиоимпульсов. Был построен график амплитудного спектра (рисунок 7.2) периодической последовательности радиоимпульсов (рисунок 7.1). Для расчёта использовались свойства преобразования Фурье.
ЗАКЛЮЧЕНИЕ
Во время выполнения курсовой работы были произведены расчеты амплитудного и фазового спектров одиночного видеоимпульса, одиночного радиоимпульса, периодической последовательности видеоимпульсов и периодической последовательности радиоимпульсов.

Для расчёта спектральной плотности одиночного видеоимпульса использовалось прямое преобразование Фурье.

Для расчёта спектральной плотности периодической последовательности видеоимпульсов использовался ряд Фурье в комплексной форме.

Для расчёта спектральной плотности одиночного радиоимпульса использовалось свойство прямого преобразование Фурье.

Для расчёта спектральной плотности периодической последовательности использовалось свойство прямого преобразование Фурье.

Даная работа подтверждает, что спектр периодического сигнала дискретен, а непериодического сигнала сплошной.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
[1] Надольский А. Н. Теоретические основы радиотехники: / А. Н. Надольский. – Минск: БГУИР, 2005.

[2] Иванов М.Т., Сергиенко А.Б., Ушаков В.Н. Теоретические основы радиотехники. Учеб. Пособие для вузов. – М.: Высш. шк., 2002.

[3] Надольский А. Н. Конспект лекций по курсу «Теоретические основы радиотехники и электроники», Минск 2019.

[4] Кауфман М. Практическое руководство по расчётам схем в электронике 1 справочник: справ.пособие / Кауфман М.,Сидман А.,1991.

---

Смотрите также файлы

• Основные черты налогового контроля в рф.docx

• Трбиені масаты мен міндеттері. Трбие.docx

• Практическая работа к теме Доверие к государству Тема занятия Наша страна россия. Класс 5.docx

• В качестве файлового сервера организации выступает сервер.docx

• О вере, неверии и сомнении Часть I. Детская вера Часть ii. Разумная вера.pdf