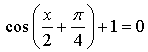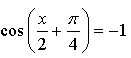ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 75
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Исследуйте функцию
на периодичность; укажите основной период, если он существует.4. Решите графически уравнение
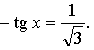
5. Постройте график функции, указанной в пункте а) или б).
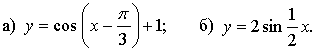
6. При каком значении параметра а неравенство имеет единственное решение? Найдите это решение.
Вариант 2
1. Не выполняя построения, установите, принадлежит ли графику функции
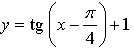точка:
2. Исследуйте функцию на четность.
3. Исследуйте функцию на периодичность; укажите основной период, если он существует.
4. Решите графически уравнение
5. Постройте график функции, указанной в пункте а) или б).
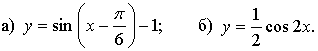
6. При каком значении параметра а неравенство имеет единственное решение? Найдите это решение.
Решение контрольной работы
Вариант 1
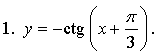
а)
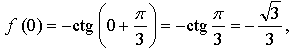значит, точка 
не принадлежит графику функции.б)
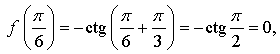значит, точка 
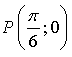принадлежит графику функции.Ответ: а) нет; б) да.
2. а)
значит, функция нечетная.
б)
f(x), значит, функция четная.в)
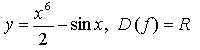
значит, функция ни четная, ни нечетная.Ответ: а) нечетная; б) четная; в) ни четная, ни нечетная.
3.
Пусть Т – основной период функции, тогда
Т = П – основной период для функции
Т = 2П – основной период для функции у = cos х.
Значит,
f(x).Ответ: Т = 2П.
4.
Построим графики функций y = tg x и
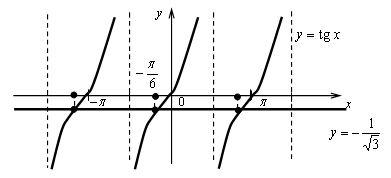
Ответ:
5. а)
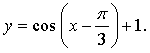
График функции получен параллельным переносом графика функции у = cos х на единиц вправо и на 1 единицу вверх.
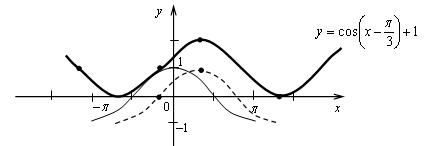
б)
График функции получен из графика функции у = sin х растяжением от оси х и от оси у в 2 раза.
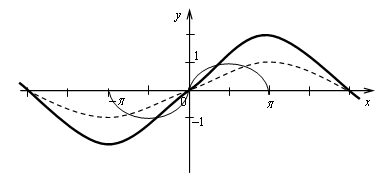
6.
у = а – х2
у = sin х
Если а < 0, то неравенство не имеет решений;
а >0, то неравенство имеет бесконечно много решений;
а = 0, то неравенство имеет единственное решение х = 0.
Ответ: а = 0.
Вариант 2
1.
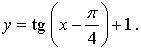
а)
значит, точка принадлежит графику функции.б)
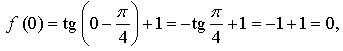значит, точка не принадлежит графику функции.Ответ: а) да; б) нет.
2. а)
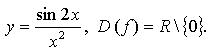
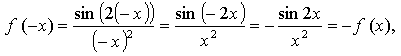значит, функция нечетная.б)
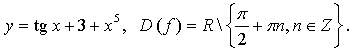
значит, функция ни четная, ни нечетная.в)
f(x), значит, функция четная.Ответ: а) нечетная, б) ни четная, ни нечетная; в) четная.
3.
Пусть Т – основной период функции, тогда
Т = П – основной период для функции у = │sin х│.
Т = 2П – основной период для функции у = cos х.
Значит,
f(x).Ответ: Т = 2П.
4.
Построим графики функций y = ctg x и
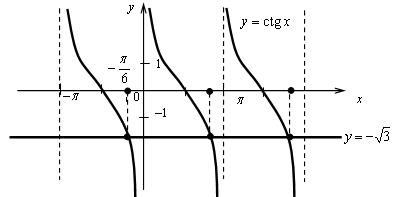
Ответ:
5. а)
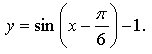
График функции получен параллельным переносом графика функции у = sin х на единиц вправо и на 1 единицу вниз.
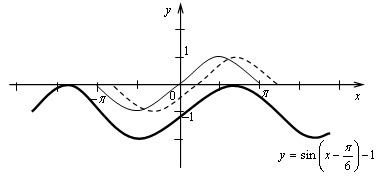
б)
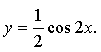
График получен сжатием графика функции у = cos 2х к оси х и к оси у в 2 раза.
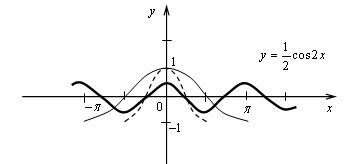
6.
у = а + х2
у = cos х
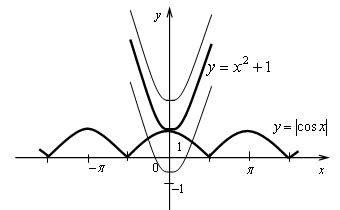
Если а >1, то неравенство не имеет решений;
а < 1, то неравенство имеет бесконечно много решений;
а = 1, то неравенство имеет единственное решение х = 0.
Ответ: а = 1.
Контрольная работа № 8 «Тригонометрические уравнения»
Вариант 1
Решите уравнения:
1.
2.
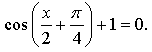
3.
4.
5. Решите уравнение:
6. Найдите корни уравнения принадлежащие отрезку
Вариант 2
Решите уравнения:
1.
2.
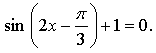
3.
4.
5. Решите уравнение:
6. Найдите корни уравнения
принадлежащие отрезку Решение заданий контрольной работы
Вариант 1
1.
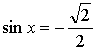
Ответ:
2.
