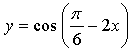6. Сумма бесконечной убывающей геометрической прогрессии равна 4, а сумма квадратов её членов равна 48. Найдите первый член и знаменатель прогрессии.

Решение вариантов контрольной работы

Вариант 1

1.







Ответ:

2. 1,(18) = 0,18 18 18 18… =

Найдем сумму бесконечной геометрической прогрессии, у которой



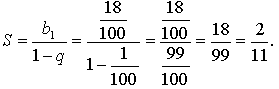
Значит, 1(18) =

Ответ:

3. а)



б)



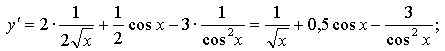
в)





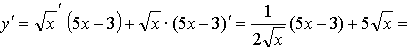
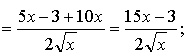
г)



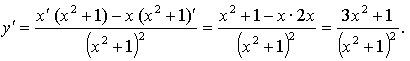
4. ,

---

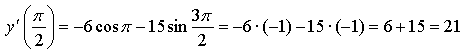
Ответ: 21.

5.

Найдем у' и подставим во второе равенство:



Имеем:





Доказано.

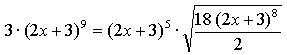
6. Пусть а_п – произвольный член геометрической прогрессии, q – знаменатель этой прогрессии.

Тогда а_{п + 1,} а_{п + 2,} а_{п + 3},… – последующие члены этой прогрессии. Найдем их сумму:



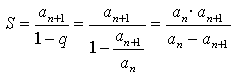
По условию а_п в 6 раз больше этой суммы. Получим уравнение:





.

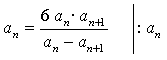
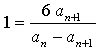
Значит, знаменатель

Ответ:

Решение вариантов контрольной работы

Вариант 1

1.







Ответ:

2. 1,(18) = 0,18 18 18 18… =

Найдем сумму бесконечной геометрической прогрессии, у которой



Значит, 1(18) =

Ответ:

3. а)

---

б)



в)





г)



4. ,





Ответ: 21.

5.

Найдем у' и подставим во второе равенство:



Имеем:





Доказано.

6. Пусть а_п – произвольный член геометрической прогрессии, q – знаменатель этой прогрессии.

Тогда а_{п + 1,} а_{п + 2,} а_{п + 3},… – последующие члены этой прогрессии. Найдем их сумму:



По условию а_п в 6 раз больше этой суммы. Получим уравнение:





.

Значит, знаменатель

Ответ:

Вариант 2

1.

---

Ответ: 5, 23, –602.

2. 0,27 = 0,27 27 27 27… =

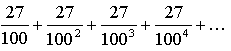
Найдем сумму бесконечной геометрической прогрессии, у которой



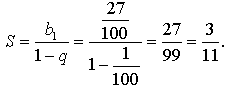
Значит, 2(27) =

Ответ:

3. а)



б)



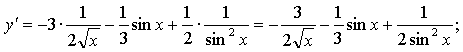
в)





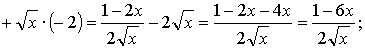
г)



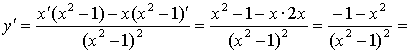
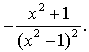
4. ,





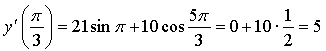
Ответ: 5.

5.

Найдем у' и подставим во второе равенство:



Имеем:

---

0 = 0. Доказано.

6. Пусть дана геометрическая прогрессия и пусть q – знаменатель этой прогрессии. Найдем её сумму, которая по условию равна 4:



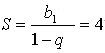
Тогда получим, что b₁ = 4(1 – q).

Последовательность, состоящая из квадратов членов данной геометрической прогрессии, в свою очередь также является геометрической прогрессией, у которой первый член равен b₁², а знаменатель равен q². Найдём сумму этой прогрессии:



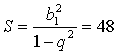
Тогда получим, что

Составим и решим уравнение:



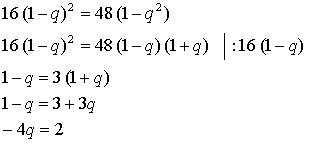
Найдем

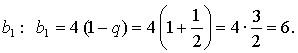
Ответ:

Контрольная работа № 14 «Применение производной для исследования функции»

Вариант 1

1. Составьте уравнение касательной к графику функции 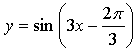в точке

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точку ппересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна биссектрисе первой координатной четверти.

Вариант 2

1. Составьте уравнение касательной к графику функции

---

Смотрите также файлы

• Реферат Тема Строительные нормы и правила, Классификация и основные части зданий и сооружений, требования к зданиям и сооружениям сдаваемым в электромонтаж.docx

• Павлова Анджела Петровна (И. О. Фамилия) Тольятти 2023 лабораторная работа.docx

• Отчет 6 Зертханалы жмыс Маманды Аспап жасау Саба Интегралды жне микропроцессорлы схемотехника.docx

• План подготовила воспитатель.docx

• 1. Минимизация отходов лесопилки.doc