ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
в точке
2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точ-кку пересечения этих касательных.
3. Исследуйте функцию на монотонность и экстремумы и постройте её график.
4. Найдите значение параметра а, при котором касательная к графику функции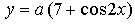 в точке с абсциссой параллельна прямой
в точке с абсциссой параллельна прямой
Решение вариантов контрольной работы
Вариант 1
1.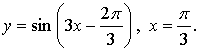
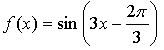
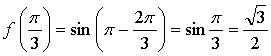
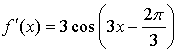
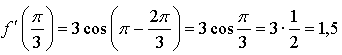
Уравнение касательной:
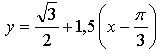
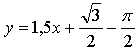
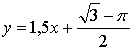
Ответ: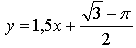
2.
Найдем точки пересечения с осью 0х:
Составим уравнение касательной в точке х = 1:
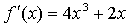
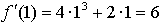
Получим,
Составим уравнение касательной в точке х = –1:
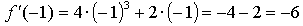
Получим
Найдем точку пересечения касательных:
х = 0
Ответ: , (0; –6).
3.
1) Область определения:
2) Чётность / нечётность:
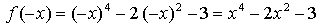 – чётная.
– чётная.
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
х = 0, х = 1
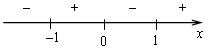
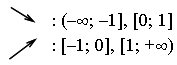
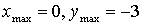
5) Контрольные точки:
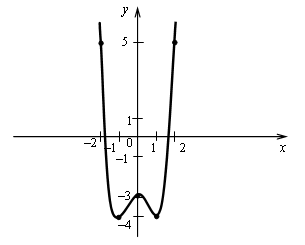
4.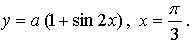
Биссектриса первой координатной четверти имеет уравнение у = х. Если касательная ей параллельна, то она имеет такой же угловой коэффициент, то есть k = 1.
Таким образом, нужно найти такое значение параметра а, при котором производная данной функции в точке равна 1.
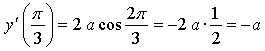
Ответ:
Вариант 2
1.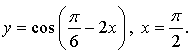
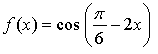
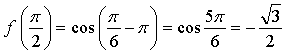
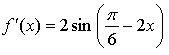
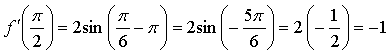
Уравнение касательной:
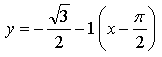
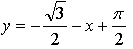
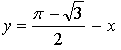
Ответ: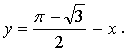
2.
Найдем точки пересечения с осью 0х:
Составим уравнение касательной в точке х = 2:
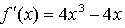
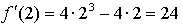
Получим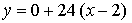
Составим уравнение касательной в точке х = –2:
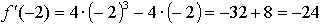
Получим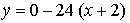
Найдем точку пересечения касательных:
х = 0
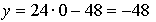
Ответ: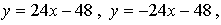 (0; –48).
(0; –48).
3.
1) Область определения:
2) Чётность / нечётность:
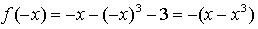 – нечётная.
– нечётная.
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
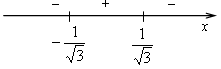
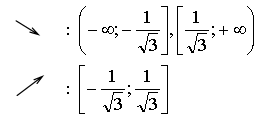
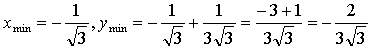
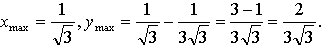
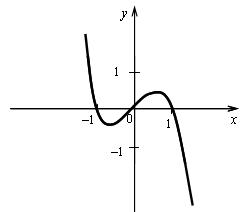
5) Контрольные точки:
Пересечение с осью 0х:
х = 0, х = 1
А (0; 0), В (1; 0), С (–1; 0).
4.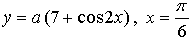
Если касательная параллельна прямой то она имеет такой же угловой коэффициент, то есть Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке равна
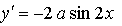
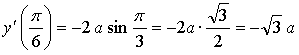
Ответ:
Контрольная работа № 15 «Вероятность событий»
ОТВЕТЫ
Контрольная работа №16 «Итоговый контроль за год»
По вариантам ЕГЭ по математике базовый уровень.
2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точ-кку пересечения этих касательных.
3. Исследуйте функцию на монотонность и экстремумы и постройте её график.
4. Найдите значение параметра а, при котором касательная к графику функции
Решение вариантов контрольной работы
Вариант 1
1.
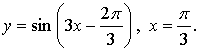
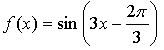
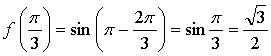
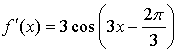
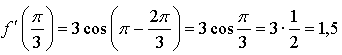
Уравнение касательной:
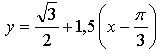
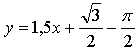
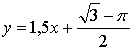
Ответ:
2.
Найдем точки пересечения с осью 0х:
Составим уравнение касательной в точке х = 1:
Получим,
Составим уравнение касательной в точке х = –1:
Получим
Найдем точку пересечения касательных:
х = 0
Ответ: , (0; –6).
3.
1) Область определения:
2) Чётность / нечётность:
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
х = 0, х = 1
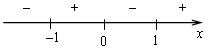
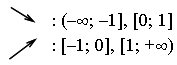
5) Контрольные точки:
| | х | 2 | |
| | у | 5 | 0 |

4.
Биссектриса первой координатной четверти имеет уравнение у = х. Если касательная ей параллельна, то она имеет такой же угловой коэффициент, то есть k = 1.
Таким образом, нужно найти такое значение параметра а, при котором производная данной функции в точке равна 1.
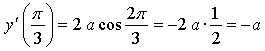
Ответ:
Вариант 2
1.
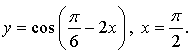
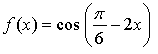
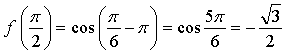
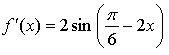
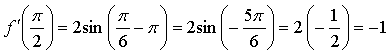
Уравнение касательной:
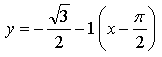
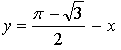
Ответ:
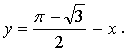
2.
Найдем точки пересечения с осью 0х:
Составим уравнение касательной в точке х = 2:
Получим
Составим уравнение касательной в точке х = –2:
Получим
Найдем точку пересечения касательных:
х = 0
Ответ:
3.
1) Область определения:
2) Чётность / нечётность:
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
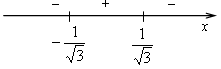
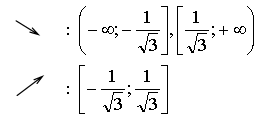
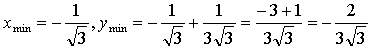
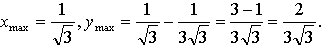
5) Контрольные точки:
Пересечение с осью 0х:
х = 0, х = 1
А (0; 0), В (1; 0), С (–1; 0).

4.
Если касательная параллельна прямой то она имеет такой же угловой коэффициент, то есть Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке равна
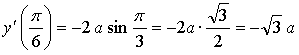
Ответ:
Контрольная работа № 15 «Вероятность событий»
| ВАРИАНТ 1
| ВАРИАНТ 2
|
ОТВЕТЫ
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 вариант | 0,995 | 0,14 | 0,93 | 0,3 | 0,06 | 0,19 | 0,25 | 0,33 |
| 2 вариант | 0,995 | 0,11 | 0,98 | 0,16 | 0,31 | 0,8836 | 0,16 | 0,125 |
Контрольная работа №16 «Итоговый контроль за год»
По вариантам ЕГЭ по математике базовый уровень.