Относительная пропускная способность – вероятность того, что заявка будет обслужена:



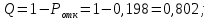
Абсолютная пропускная способность:



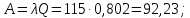
Среднее число занятых каналов:

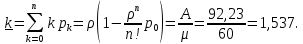
Задание 5.

Анализируется работа международного телефонного пункта в небольшом городке. Пункт имеет только один телефонный аппарат (одноканальная СМО). В среднем за сутки поступает λ = 216 заявок. Никаких ограничений на длину очереди нет. Средняя продолжительность переговоров 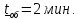Определить финальные вероятности состояний S₀, S₁, S₂ и характеристики эффективности СМО (среднее число заявок в системе и очереди, среднее время пребывания заявки в системе и очереди).

Решение:

Исчисляем показатели обслуживания для одноканальной СМО.



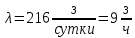
Интенсивность потока обслуживания:



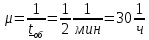
Интенсивность нагрузки:



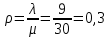
Интенсивность нагрузки ρ = 0,3 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.

Поскольку ρ < 1, то очередь не будет расти бесконечно, следовательно, предельные вероятности существуют.

3. Вероятность, что канал свободен (доля времени простоя канала).





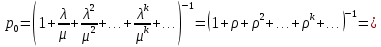
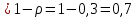
Следовательно, 70% в течение часа канал будет не занят, время простоя равно t_пр = 42 мин.

Вероятность того, что в очереди:

1 заявка:



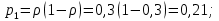
2 заявки:

---

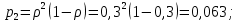
3 заявки:



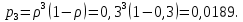
4. Доля заявок, получивших отказ.

p₁ = 1 - p₀ = 1 – 0,7 = 0,3

Значит, 30% из числа поступивших заявок не принимаются к обслуживанию.

5. Относительная пропускная способность.

Поскольку в рассматриваемой СМО ограничение на длину очереди отсутствует, то любая заявка может быть обслужена, поэтому Q = p_обс = 1.

6. Абсолютная пропускная способность.



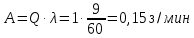
8. Среднее число заявок в очереди (средняя длина очереди).



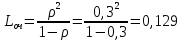
9. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди).



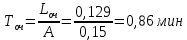
10. Среднее число обслуживаемых заявок.

L_об = ρ = 0,3

12. Среднее число заявок в системе L_сист определим по формуле:



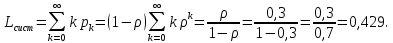
13. Среднее время пребывания заявки в СМО.

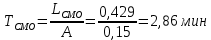
Задание 6.

Задача 1. Фирма ставит цели: улучшить качество до заданного уровня (W₁), увеличить объем производства до заданного уровня (W₂) и разработать новую модификацию товара (W₃). Первая и вторая цели – третьего типа формулировки, а третья – второго. Коэффициенты весомости а₁ = 0,5; а₂ = 0,2; а₃ = 0,3. Результаты применения различных стратегий приведены в таблице.

Стратегии	W1	W2	W3	W
S1	0,8	0,5	0
S2	0,8	0,3	1
S3	0,5	0,4	0
S4	0,8	0,5	1

Рассчитать значения обобщенного критерия, заполнив последний столбец таблицы и выбрать оптимальную стратегию.

Решение.

Сократим количество допустимых стратегий с помощью правила их отсева: если для одной стратегии показатели всех критериев лучше, чем для другой, то последнюю стратегию можно исключить из рассмотрения. Стратегия S

---

₃ по всем критериям хуже S₄, поэтому, ее исключим из анализа.

Обобщенный критерий определяется по формуле:



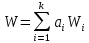
где a_i – коэффициент важности критерия W_i.

Например, для 1-й стратегии:

W = 0,5·0,8 + 0,2·0,5 + 0,3·0 = 0,5

Аналогичным образом определим для остальных рассматриваемых стратегий, результаты заполним в последнем столбце таблицы:

Стратегии	W1	W2	W3	W
S1	0,8	0,5	0	0,5
S2	0,8	0,3	1	0,76
S4	0,8	0,5	1	0,8

Наибольшее значение обобщенного критерия для стратегии S₄, поэтому, фирма выбирает ее.
Задача 2. Фирма ставит цели: увеличить прибыль (W₁), увеличить объем производства (W₂), снизить себестоимость продукции (W₃) и увеличить долю рынка (W₄). Величина уступки – 10% от наилучшего значения. Исходные данные приведены в таблице.

Стратегии	W1, млн.р.	W2, тыс.шт.	W3, р.	W4, %
S1	10	300	10	5
S2	12	120	70	3
S3	15	180	100	10
S4	14,5	190	108	2
S5	14	150	20	7

Решить задачу выбора оптимальной стратегии методом последовательных уступок.

Решение.

Наибольшее значение прибыли W₁^* = 15 млн.руб. при стратегии S₄. На эту величину накладываем уступку 10%:



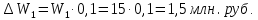
Следовательно, значение W₁ должно быть не менее 15 – 1,5 = 13,5 млн.руб. этому условию удовлетворяют стратегии S

---

₃, S₄ и S₅.

Среди оставшихся трех стратегий ищется стратегия, дающая наибольший объем производства – S₄ (со значением W₂ = 190 тыс.шт.). На величину W₂ дается уступка в размере 10%:



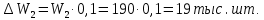
Остаются две стратегии, при которых величина объема производства не менее 171 тыс.шт. - S₃, S₄.

Среди оставшихся двух стратегий ищется стратегия, дающая наименьшую себестоимость продукции – S₃ (со значением W₃ = 100 р.). На величину W₃ дается уступка в размере 10%:



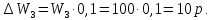
Остаются две стратегии, при которых себестоимость продукции менее 110 р. - S₃, S₄.

Среди оставшихся двух стратегий ищется стратегия, дающая наибольшую долю рынка – S₃ (со значением W₄ = 10%.). На величину W₃ дается уступка в размере 10%:



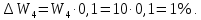
Остается одна стратегия, при которой доля рынка не менее 9% - S₃, которую фирма и выбирает.
Задача 3. Решить предыдущую задачу методом сведения целей в ограничения, задав следующие ограничения:



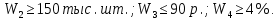
Решение.

Для выбора стратегии применим метод сведения целей в ограничения. В качестве главного критерия будем рассматривать величину прибыли, а на объем производства (W₂), себестоимость продукции (W₃) и долю рынка (W₄) наложим следующие ограничения:

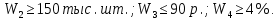
Стратегии	W1, млн.р.	W2, тыс.шт.	W3, р.	W4, %
S1	10	300	10	5
S2	12	120	70	3
S3	15	180	100	10
S4	14,5	190	108	2
S5	14	150	20	7

---

Из таблицы видно, что принятым ограничениям удовлетворяют стратегии S₁ и S₅, а по критерию прибыли оптимальной стратегией является S₅

---

Смотрите также файлы

• По каким признакам можно понять, будет ли человек получать удовлетворение от работы в качестве менеджера или нет.docx

• Методические рекомендации по выполнению рейтинговой (контрольной) работы по дисциплине Административное право.docx

• Повседневная жизнь средневекового города в Европе и Древней Руси.pdf

• Продолжение вопроса 1.pdf

• 21ЗБ11 Чернецкая Мария.docx