Файл: Кафедра физики расчётнографическая работа 1 Вариант 8 Мальцева Ю. Е. Группа зи221 Номер студенческого билета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 146
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Свободные незатухающие колебания.
Механические колебания.
В механических системах при отсутствии сил трения и сил сопротивления возникают свободные незатухающие колебания под действием упругих сил Fупр(Рис.7.1) или квазиупругих сил Pп (Рис.7.2).
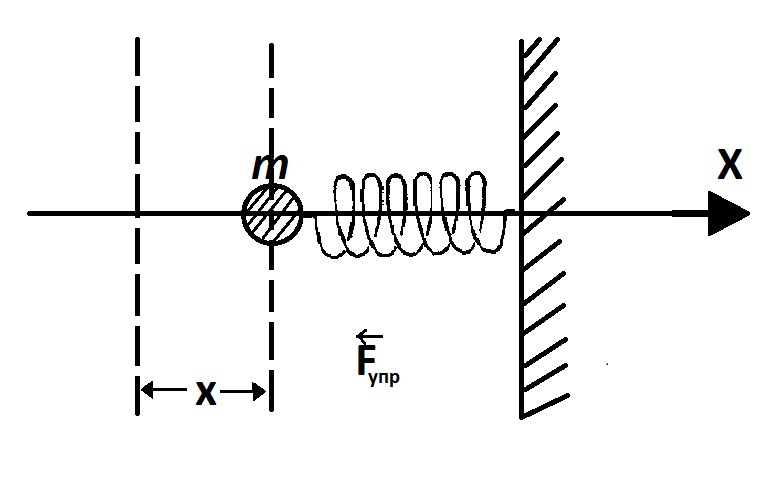
Рис.7.1 Пружинный маятник.
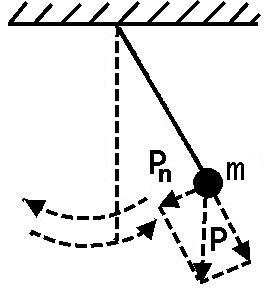
Рис.7.2 Математический маятник. Сила тяжести играет роль квазиупругой силы.
Дифференциальное уравнение свободных незатухающих колебаний
Данное уравнение можно получить, рассматривая колебания пружинного маятника, которые возникают под действием упругой силы
F упр = - kx. (7.1)
где х – смещение тела от положения равновесия; k – коэффициент упругости пружины.
Согласно II закону Ньютона
????упр = ???????? (7.1*)
где a – ускорение, сообщаемое упругой или квазиупругой силой; m – масса тела, которое совершает колебания.
Квазиупругими называют силы, независимо от их природы, для которых модуль силы пропорционален величине отклонения системы от равновесного положения.
По определению, ускорение — это вторая производная координаты по времени:
a =
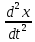 , (7.2)
, (7.2) Тогда объединяя (7.1), (7.1*) и (7.2), получим
- kx = m
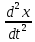 (7.3)
(7.3) Разделив левую и правую часть (7.3) на m, получим
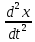 +
+ 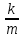 x = 0 (7.4)
x = 0 (7.4)Обозначим
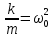 , где
, где 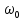 =
= 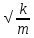 - собственная частота колебаний системы,
- собственная частота колебаний системы, После введения данных обозначений уравнение (7.4) примет вид:
 +
+ 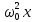 = 0 (7.5)
= 0 (7.5) Уравнение (7.5) называется дифференциальным уравнением свободных незатухающих колебаний.
Уравнение колебаний
Решением дифференциального уравнения является выражение:
X= Acos(
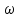 0t+
0t+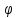 0) (7.6)
0) (7.6) В этом уравнении колебаний А-амплитуда колебания, равная максимальному смещению тела, совершающего колебания, от положения равновесия; (
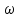 0t+
0t+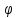 0) - фаза колебаний,
0) - фаза колебаний, 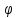 0 - начальная фаза колебаний, которая определяется начальным положением тела ( т.е. при t = 0).
0 - начальная фаза колебаний, которая определяется начальным положением тела ( т.е. при t = 0). Скорость и ускорение при гармонических колебаниях
Если уравнение смещения дано в виде
X= Acos (
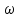 0t+
0t+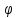 0)
0)то скорость υ будет равна первой производной от смещения по времени, т.е.
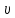 =
= 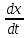 = -A
= -A sin (
sin (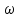 0t +
0t +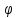 0)
0)где A
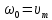 - амплитудное (максимальное) значение скорости. Тогда зависимость скорости от времени запишется в виде:
- амплитудное (максимальное) значение скорости. Тогда зависимость скорости от времени запишется в виде: υ =
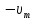 sin (
sin (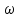 0t+
0t+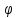 0) (7.7)
0) (7.7) Ускорение — это вторая производная от смещения по времени
a =
 = - A
= - A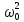 cos (
cos (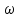
0t +
 0)
0)где
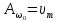 - амплитудное значение ускорения. Тогда зависимость ускорения от времени запишется в виде:
- амплитудное значение ускорения. Тогда зависимость ускорения от времени запишется в виде: a = -
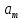 cos
cos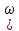 0t+
0t+ 0) (7.8)
0) (7.8) Энергия колебания тела.
Отклонив пружинный маятник от положения равновесия, ему сообщают потенциальную энергию, которая определяется по формуле kx2
Wп =
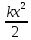 (7.9)
(7.9) При колебаниях маятник будет обладать энергией W мех, которая в любой момент времени представляет сумму потенциальной (Wп) и кинетической (Wкин) энергии:
Wмех =Wп +Wкин (7.10)
В изолированной системе полная энергия остается постоянной при любых взаимодействиях внутри системы: ΔWмех = 0 (изменения энергии системы нет).
Если смещение меняется по закону x = Acos
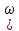 0t+
0t+ 0), то его кинетическая энергия будет равна
0), то его кинетическая энергия будет равна Wкин =
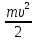 =
= 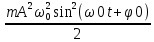
Так как m
 = k, то зависимость кинетической энергии от времени запишется так:
= k, то зависимость кинетической энергии от времени запишется так: Wкин =
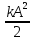
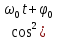 )
)Потенциальная энергия пружинного маятника с учетом (7.6) зависит от времени так:
Wn =
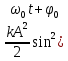 )
)В положении наибольшего отклонения тело имеет максимальную потенциальную энергию
Wп m =
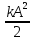 ,
,А кинетическая энергия в этот момент времени равна 0. При прохождении телом положения равновесия его кинетическая энергия будет максимальной kA2
Wкинm =
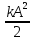
,
а потенциальная энергия равна 0, следовательно, полная механическая энергия Wполн.мех. пружинного маятника без трения равна:
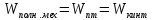 (7.11)
(7.11) Незатухающие колебания в электрическом контуре
В электрическом контуре, содержащем индуктивность и емкость, при отсутствии омического сопротивления, возникают незатухающие электромагнитные колебания: заряд, разность потенциалов на обкладках (напряжение) конденсатора, ток в катушке меняются по гармоническому закону.
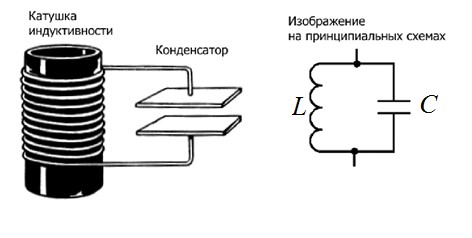
Рис. 7.3 Колебательный контур (сопротивление R = 0
Дифференциальное уравнение колебания заряда.
Для математического описания электрических процессов в контуре применим 2 правило Кирхгофа: «Сумма падений напряжения в контуре равна сумме действующих в нем ЭДС». В идеальном колебательном контуре падение напряжения на конденсаторе UC. При изменении силы тока в контуре в катушке индуктивности возникает ЭДС самоиндукции
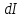 .
. UC = - L
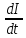 (7.12)
(7.12)Напряжение на конденсаторе равно UC =
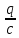 , а сила тока по определению связана с зарядом конденсатора соотношением: I =
, а сила тока по определению связана с зарядом конденсатора соотношением: I = 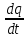
Подставив выражения для тока I и напряжения UC в формулу (7.12) и перенеся все члены в левую часть уравнения, получим дифференциальное уравнение в виде:
L
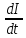 +
+ 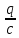 = 0
= 0Разделим уравнение на коэффициент при старшей производной (индуктивность катушки) и введем обозначение:
 =
= 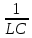
После введения обозначений дифференциальное уравнение гармонических колебаний в контуре принимает вид:
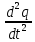 =
= 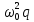 =0 (7.13)
=0 (7.13)где
