Файл: Управление финансовыми рисками наукоёмких организаций.doc
Добавлен: 04.12.2023
Просмотров: 201
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Дополнительные задачи
по дисциплине "Управление финансовыми рисками наукоёмких организаций"
1. Оценка риска портфеля ценных бумаг
Задача 1.1. Менеджер управлял портфелем ценных бумаг в течение 4 лет. Начальные инвестиции составили 20 млн. руб. В конце первого года стоимость портфеля выросла до 21 млн. руб. В начале второго года дополнительно приобретено ценных бумаг на сумму в 2 млн. руб. В конце второго года стоимость портфеля составила 26 млн. руб. В начале третьего года произведена продажа ценных бумаг из состава портфеля, сократившая его стоимость на 3 млн. руб. В конце третьего года стоимость портфеля составила 25 млн. руб. В начале четвёртого года дополнительно приобретено ценных бумаг на сумму в 2 млн. руб. В конце года стоимость портфеля составила 30 млн. руб. Определить риск портфеля, измеренный выборочным стандартным отклонением.
Решение. Составляется статистический ряд годовых доходностей портфеля ценных бумаг. С этой целью производится расчёт этих доходностей:
; 
;
; 
.Рассчитывается выборочное стандартное отклонение за год на основе полученных доходностей:
;
;
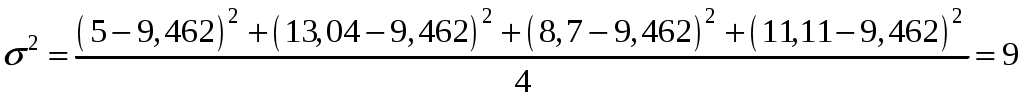.Задача 1.2. Фактическая доходность портфеля А равна 21 %, стандартное отклонение доходности равно 14 %. Доходность и стандартное отклонение портфеля В соответственно равны 25 % и 18 %. Безрисковая процентная ставка равна 8 % годовых. Определить с помощью коэффициента Шарпа, какой портфель управлялся эффективнее.
Решение.
; 
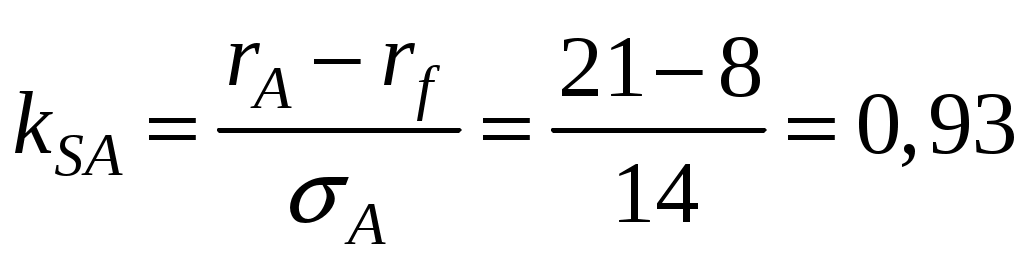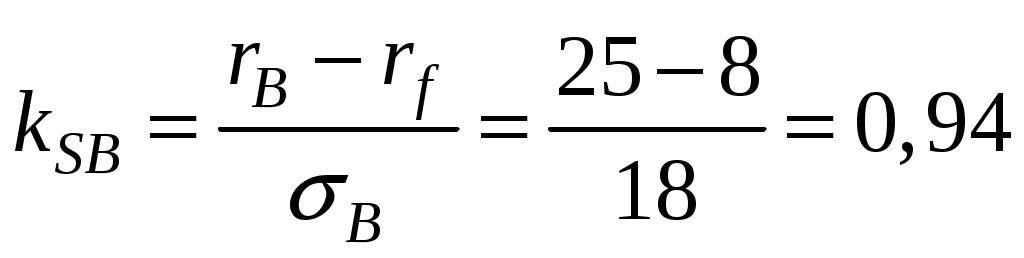.Портфель В управлялся эффективнее.
Задача 1.3. В начале года размер инвестиций в портфель ценных бумаг составил 30 млн. руб. По окончании первого квартала стоимость портфеля составила 32 млн. руб. На следующий день дополнительно было приобретено ценных бумаг на сумму 4 млн. руб. По окончании второго квартала стоимость портфеля составила 35 млн. руб., и он был увеличен ещё на 2 млн. руб. По окончании третьего квартала стоимость портфеля составила 37 млн. руб., и часть ценных бумаг из его состава на сумму 2 млн. руб. были проданы. В конце года стоимость портфеля составила 38 млн. руб. Безрисковая процентная ставка равна 8 % годовых. Определить коэффициент Шарпа портфеля в годовом исчислении (в задаче использовать выборочное стандартное отклонение).
Решение.
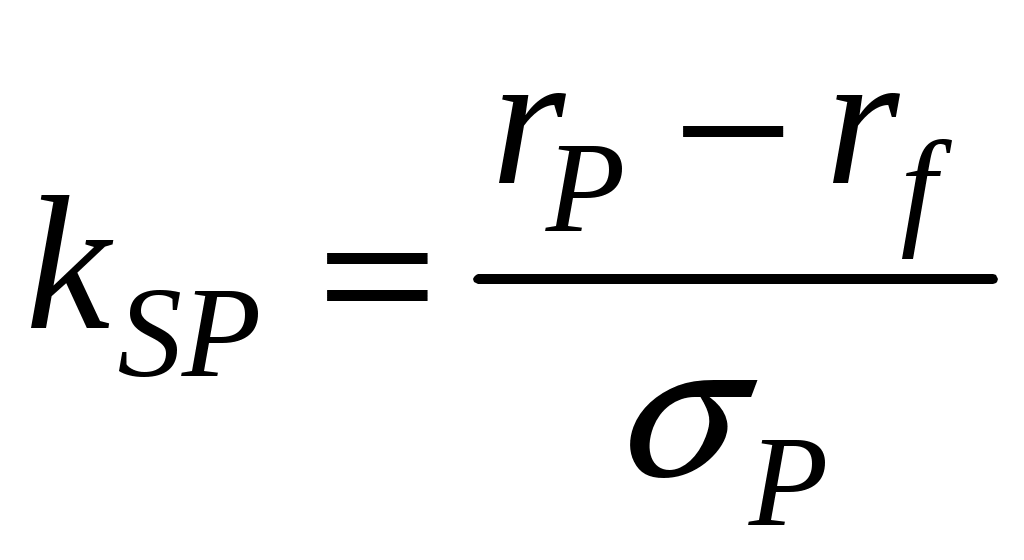,где
- коэффициент Шарпа портфеля ценных бумаг;
- годовая доходность портфеля ценных бумаг;
- безрисковая процентная ставка;
- выборочное стандартное отклонение (риск) портфеля ценных бумаг в годовом исчислении.
;
(
- стандартное отклонение доходности портфеля за квартал).Для расчёта
необходимо построить статистический ряд квартальных доходностей:
; 
; 
; 
;
;
;
; 
;
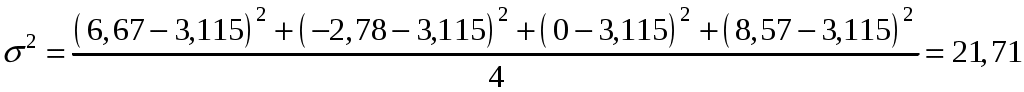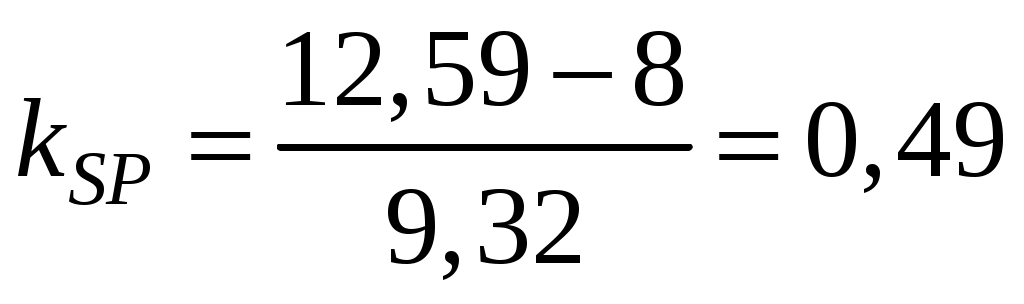.Задача 1.4. Инвестор приобретает рискованный актив А по 800 тыс. руб. за счёт собственных средств, занимает 200 тыс. руб. под 12 % годовых и также инвестирует их в актив А. Ожидаемая доходность актива А равна 30 % годовых, стандартное отклонение доходности 20 %. Какую доходность может получить инвестор через год с вероятностью 68,3 %. Доходность актива распределена нормально.
Решение. Можно ожидать, что с вероятностью 68,3 % доходность портфеля через год будет находиться в интервале
относительно ожидаемой доходности 
. Поэтому необходимо рассчитать стандартное отклонение доходности портфеля 
и .
.Удельный вес актива А в портфеле
равен 
Удельный вес занятых средств в портфеле
равен 
Так как дисперсия заёмных средств равна нулю
и ковариация доходности актива А с заёмными средствами равна нулю 
, то дисперсия доходности портфеля будет равна 
.Ожидаемая доходность портфеля равна
.Таким образом через год доходность портфеля с вероятностью 68,3 % будет находиться в интервале
или от 
до 
.Задача 1.5. Инвестор приобретает рискованный актив А на 300 тыс. руб. и актив В на 200 тыс. руб. за счёт собственных средств, занимает 200 тыс. руб. под 12 % годовых и покупает на 150 тыс. руб. актив А и на 50 тыс. руб. актив В. Ожидаемая доходность актива А равна 20 %, актива В - 15 % годовых, стандартное отклонение доходности актива А в расчёте на год составляет 14 %, актива В - 10 %, ковариация доходностей активов равна 0,7. Какую доходность может получить инвестор через год с вероятностью 95,4 %. Доходности активов распределены нормально.
Решение. Можно ожидать, что с вероятностью 95,4 % доходность портфеля через год будет находиться в интервале
относительно ожидаемой доходности 
. Поэтому необходимо рассчитать стандартное отклонение доходности портфеля и .Удельный вес актива А в портфеле
равен 
Удельный вес актива Bв портфеле
равен 
Удельный вес занятых средств в портфеле
равен 
Таким образом через год доходность портфеля с вероятностью 95,4 % будет находиться в интервале
или от 
до 
.2. Расчёт показателя VaR
Задача 2.1. Определить однодневный VaRс доверительной вероятностью 90 % для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчёте на день равно 1,5 %.
Решение.
,где
- 
портфеля;
- стоимость портфеля;
- стандартное отклонение доходности портфеля, соответствующее времени, за которое рассчитывается 
;
- квантиль (количество стандартных отклонений, соответствующее уровню доверительной вероятности 
). Для 
.
Задача 2.2. Определить однодневный VaRс доверительной вероятностью 95 % для портфеля стоимостью 10 млн. руб., в который входят акции двух компаний. Удельный вес первой акции в стоимости портфеля составляет 60 %, второй - 40 %. Стандартное отклонение доходности первой акции в расчёте на один день равно 1,58 %, второй акции - 1,9 %, коэффициент корреляции доходностей акций равен 0,8.
Решение. Определяется стандартное отклонение доходности портфеля:
.Определяется VaRпортфеля:
Задача 2.3. Портфель инвестора состоит из акций компаний А и В. Коэффициент корреляции между доходностями этих акций равен 0,4. Однодневный
с доверительной вероятностью 95 % по акциям компании А равен 20 тыс. руб., а однодневный 
с доверительной вероятностью 95 % по акциям компании В равен 30 тыс. руб. Определить 
портфеля, состоящего из данных бумаг.Решение.
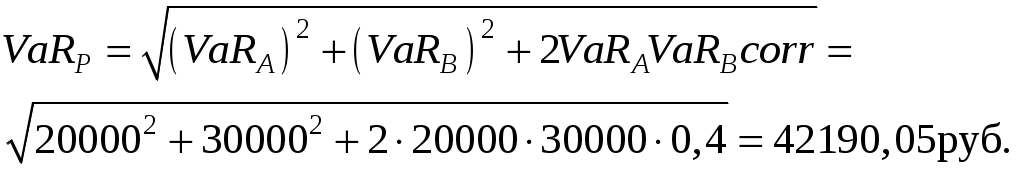
Задача 2.4. Портфель инвестора состоит из акций компаний А и В. Коэффициент корреляции между доходностями этих акций равен 0,6. Однодневный