Файл: Руководство по выражению неопределенности измерения гост р исо 110952007 Статистические методы. Линейная калибровка с использованием образцов сравнения.docx

ДОКУМЕНТИРОВАННАЯ ПРОЦЕДУРА«Оценивание неопределённости измерений»

ОГЛАВЛЕНИЕ

1. Назначение и область применения

Настоящая процедура (далее – Процедура) описывает правила оценивания и выражения неопределенности методик измерений в Испытательной лаборатории.Инструкция предназначена для сотрудников ИЛ.

2. Нормативные ссылки

• 
  ГОСТ ISO/IEC 17025-2019 «Общие требования к компетентности испытательных и калибровочных лабораторий»;
  
• 
  ГОСТ 34100.3-2017 «Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения»;
  
• 
  ГОСТ Р ИСО 11095-2007 «Статистические методы. Линейная калибровка с использованием образцов сравнения»;
  
• 
  РМГ 29-2013 «ГСИ. Метрология. Основные термины и определения»;
  
• 
  РМГ 91-2019 «ГСИ. Использование понятий «погрешность измерения» и «неопределенность измерений». Общие принципы»;
  
• 
  Р 50.2.038-2004 «ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений»;
  
• 
  Р 50.2.028-2003 «ГСОЕИ. Алгоритмы построения градуировочных характеристик средств измерений состава веществ и материалов и оценивание их погрешностей (неопределенностей). Оценивание погрешности (неопределенности) линейных градуировочных характеристик при использовании метода наименьших квадратов»;
  
• 
  Руководство ЕВРАХИМ/СИТАК CG 4. «Количественное описание неопределенности в аналитических измерениях;
  
• 
  МИ 1317-2004 «ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров».
  

---

3. Термины, определения и сокращения

Измерение – получение численного значения измеряемой величины, в том числе и в процедурах испытаний, анализа, контроля.Результат (результат измерения величины) – множество значений величины, приписываемых измеряемой величине вместе с любой другой доступной и существенной информацией. В большинстве случаев информация относится к точности измерения и выражается показателями точности, в обоснованных случаях содержит указание методики измерений и др.Неопределённость измерения– параметр, относящийся к результату измерения и характеризующий разброс (рассеяние) значений, которые могли бы быть обоснованно приписаны измеряемой величине.Стандартная неопределённость – неопределенность результата измерения, выраженная в виде стандартного отклонения.Суммарная стандартная неопределённость – стандартная неопределенность измерений, которую получают суммированием отдельных стандартных неопределенностей измерений, связанных с входными величинами в модели измерений.Расширенная неопределённость – величина, определяющая интервал вокруг результата измерения, который, как ожидается, содержит в себе большую часть распределения значений, которые с достаточным основанием могут быть приписаны измеряемой величине.Коэффициент охвата – коэффициент, на который умножают суммарную стандартную неопределенность для получения расширенной неопределенности.Бюджет неопределённости – перечень источников неопределенности с соответствующими им стандартными неопределенностями, составленный для определения оценки суммарной стандартной неопределенности результата измерений.

---

ИЛ – испытательная лаборатория;КХА – количественный химический анализ;МВИ – методика выполнения измерений;СИ – средство измерений;СКО – среднее квадратическое отклонение;МНК – метод наименьших квадратов;ММК – метод Монте-Карло.

4.   1   2   3   4

---

Процедура

1. Общие положения. Понятия «погрешность» и «неопределенность».

Одним из ключевых положений ГОСТ ISO/IEC 17025-2019 является требование к испытательным лабораториям оценивать неопределенность измерений. В случае если хорошо известный метод испытаний устанавливает пределы значений основных источников неопределенности измерений и указывает форму представления результатов вычислений, то считается, что лаборатория выполнила требования оценке неопределённости измерений.Одновременно в большинстве аттестованных методик измерений, используемых при испытаниях, в качестве показателей точности определены приписанные показатели качества на основе характеристики погрешности. Это обусловлено тем, что концепция неопределённости используется сравнительно недавно в нашей стране. Вместе с тем существует определённая связь между этими двумя концепциями статистической оценки результатов измерений. Что бы уяснить её, рассмотрим базовые основы теории.Фундаментальным понятием классической теории измерений является погрешность: 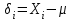(1)отклонение результата измерения X_i от истинного значения измеряемой величины μ. Погрешность возникает из-за несовершенства процесса измерений. Хотя погрешность не может быть точно известна (из-за неизвестности истинного значения), это понятие удобно использовать для статистического описания процесса измерений.Рассмотрим теперь, как определяется неопределенность. Согласно руководству ЕВРАХИМ/СИТАК «Количественное описание неопределённости в аналитических измерениях», неопределенность - это «Параметр, связанный с результатом измерения и характеризующий разброс значений, которые с достаточным основанием могут быть приписаны измеряемой величине. … Этим параметром может быть, например, стандартное отклонение или ширина доверительного интервала».Согласно другим определениям – неопределенность следует рассматривать как «параметр центрированной случайной величины, представляющей собой разность между истинным значением измеряемой величины и результатом измерений, то есть величины, совпадающей по модулю с погрешностью измерений, но противоположной ей по знаку». Другими словами, это параметр распределения величины

---

.

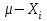
Таким образом, различие между традиционным подходом, использующим понятие «погрешность измерений» и подходом «неопределённость» сводится к различию систем координат, относительно которых рассматривают значение измеряемой величины и результат измерений. Из этого следует, что количественно характеристики погрешности измерений и соответствующие виды неопределенности измерений совпадают. Подробнее о соответствии различных форм представления показателей качества написано в РМГ 61-2010.

2. Оценка неопределённости для МВИ с установленной погрешностью.

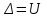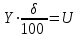Если результат измерения получен по методу (ГОСТ, ПНД Ф, МУ и т.п.) с установленными границами погрешности, то их значения принимаются равными расширенной неопределённости. или , (2)где Δ – границы абсолютной погрешности,δ – границы относительной погрешности,Y – результат измерений,U – расширенная неопределённость.

3. Оценка неопределённости МВИ.

   1. Метод моделирования для оценки неопределённости измерений.

Метод моделирования является наиболее разработанным и широко используемым для оценки неопределенности измерений. Он заключается в установлении модели измерений, которая связывает измеряемую величину с влияющими величинами, расчете стандартной неопределенности каждой влияющей величины и оценке с учетом весовых коэффициентов (коэффициентов чувствительности) стандартной неопределенности измеряемой величины. При использовании этого метода предполагается, что поправки на значимые систематические эффекты включены в модель. 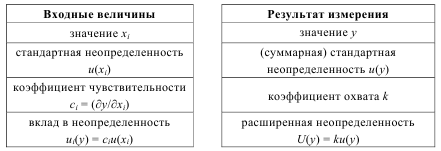Применение закона распространения неопределенности дает возможность оценить суммарную неопределенность, связанную с результатом.Типичными выходными данными подхода моделирования является «бюджет неопределенности», дающий возможность получить итоговую оценку суммарной стандартной неопределенности результата измерения из неопределенностей входных величин. Бюджет неопределенности включает данные о каждой «входной величине» и ее вкладе в результат измерения и неопределенность и сами данные о результате измерения и ее неопределенности, как показано ниже на схеме.

---