Файл: Руководство по выражению неопределенности измерения гост р исо 110952007 Статистические методы. Линейная калибровка с использованием образцов сравнения.docx

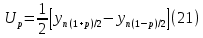
где y_n(1+p)/2 и y_n(1-p)/2 – соответствующие члены упорядоченного массива данных выходной величины. Для P = 0,95 и n = 10⁵ для расчёта берут 97500 и 2500 член упорядоченного массива выходной величины.

- оценку коэффициента охвата

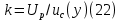
3. Метод электронных таблиц для вычисления неопределенности.

В программе Excel можно реализовать непосредственное вычисление вкладов неопределённости, без определения коэффициентов чувствительности. Для этого используют метод частных приращений.

Его суть заключается в использовании формулы:

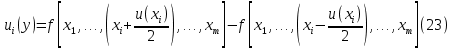
4. Представление неопределенности, зависящей от результата измерений.

В химических измерениях часто наблюдается, что доминирующие вклады в общую неопределенность изменяются примерно пропорционально содержанию аналита в широком диапазоне значений. В таких случаях имеет смысл приводить неопределенность в виде относительной расширенной неопределённости. Если неопределенность не зависит от содержания аналита, то обычно приводят абсолютное значение неопределенности.

Чтобы учесть как пропорциональную зависимость, так и возможность примерно постоянного значения неопределенности при изменении содержания, используется следующее общее выражение:

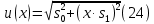
где u(x) – суммарная стандартная неопределенность результата x; s₀ – постоянная составляющая неопределенности; s₁ – коэффициент пропорциональности.

Это выражение основано на обычном методе сложения двух составляющих суммарной неопределенности в предположении, что одна составляющая (s₀) является постоянной, а другая (xs₁) пропорциональна содержанию.

Такой подход применим только тогда, когда можно получить достаточно большое число точек для построения графика зависимости. В действительности в экспериментальных исследованиях нечасто есть возможность набрать большую статистику данных. При таких обстоятельствах адекватное приближение можно получить с помощью простой линейной регрессии, включающей четыре или более значений суммарной неопределенности, полученных при различных концентрациях аналита. В этом случае зависимость задаётся выражением

---

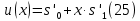
В общем случае, неопределенности могут быть представлены в виде значений s′₀ и s′₁. Эти значения можно использовать для того, чтобы дать оценку неопределенности в области применения методики.

В частных случаях возможны следующие упрощения выражения (25):

• 
  Неопределенность не зависит от содержания аналита (преобладает слагаемое s′₀). При этих обстоятельствах значение s′₁ можно принять равным нулю. s′₀ представляет собой вычисленную стандартную неопределенность.
  
• 
  Неопределенность явно зависит от содержания аналита (преобладает слагаемое s′₁). При этих обстоятельствах, а также когда область применения методики не охватывает близкие к нулю содержания, s′₀ с достаточным основанием можно принять равным нулю, a s′₁ будет просто представлять собой относительную неопределенность.
  

4. 1   2   3   4

---

Практические аспекты оценки неопределённости КХА.

1. Источники неопределенности при проведении КХА.

Типичными источниками при проведении количественных химических измерений являются неопределенности оценивания:

1) массы;

2) объема раствора (жидкости);

3) степени чистоты реактива;

4) значения эталонного образца;

5) градуировочной функции;

6) эквивалентного объема титранта;

7) погрешности средств измерений и испытательного оборудования;

8) влияния случайных факторов и др.

Более подробное описание каждого из возможных источников и их количественная оценка представлены ниже.

1) Неопределенность оценивания массы.

Неопределенность, связанную с нахождением массы анализируемой навески, оценивают исходя из данных о погрешности весов, которые, как правило, приведены в свидетельстве о поверке или калибровке весов или в документации производителя.

ПРИМЕР 1. Необходимо оценить стандартную неопределенность массы навески m = 30,2378 г, которую определяли с помощью весов лабораторных модели ВЛР-200г-М 2-го класса точности с пределом допускаемой погрешности Δm = ±0,0005 г.

Предполагая равномерный закон распределения погрешности весов, стандартную неопределенность массы вычисляют по уравнению

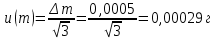
2) Неопределенность оценивания объема жидкости.

Объем жидкости, находящейся в мерной посуде, подвержен влиянию двух основных источников неопределенности: калибровка и влияние температуры.

ПРИМЕР 2. Необходимо рассчитать стандартную неопределенность объема воды, в котором растворяли навеску вещества, при этом использовали мерную колбу исполнения 1, вместимостью 100 мл, 1-го класса точности (1-100-1 ГОСТ 1770–74).

Калибровка. Стандартная неопределенность u(V_k) вычисляется исходя из предположения о треугольном распределении вероятностей отклонения объема от заявленной вместимости. Выбор треугольного распределения, а не прямоугольного (равномерного), обусловлен тем, что технологически, в процессе производства мерной посуды, номинальные значения объёма более вероятны, чем крайние.

В данном случае для колбы 1-100-1 ГОСТ 1770–74 допустимая погрешность равна 0,1 мл, а стандартная неопределенность:

---

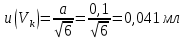
Влияние температуры. Мерную стеклянную посуду калибруют при температуре 20 °С, в то время как температура в лаборатории колеблется в пределах 20±5 °С. Коэффициент объемного расширения воды и, следовательно, водных растворов равен α=2,1·10^–4 °С^–1. Возможные колебания объема a из-за различия температуры, при которой проводятся испытания, от температуры, при которой калибруется мерная посуда, определяют по формуле

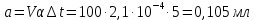
Исходя из прямоугольного распределения вероятностей, стандартная неопределенность, связанная с изменением температуры, составит:


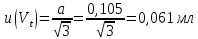
Эти два вклада суммируют, получая стандартную неопределенность объема u(V):

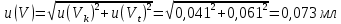
3) Неопределенность оценивания степени чистоты реактива.

Стандартную неопределенность чистоты реактива u(P), или неопределенность содержания вещества в реактиве, рассчитывают исходя из информации о степени его чистоты или содержании основного вещества, указанных в сертификате производителя или другой документации.

ПРИМЕР 3. Необходимо рассчитать стандартную неопределенность чистоты гидроксида натрия марки х. ч. по ГОСТ 4328–77.

Паспортное значение массовой доли основного вещества – 99,8%. В соответствии с ГОСТ 4328–77, допускаемая относительная суммарная погрешность результата анализа ±0,6 % при доверительной вероятности Р = 0,95.

Абсолютная погрешность содержания гидроксида натрия составит:

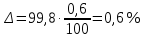
Стандартная неопределенность u(P) рассчитывается исходя из нормального закона распределения (так как известны границы погрешности и доверительная вероятность Р):

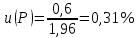
или в неименованных относительных единицах:



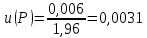
4) Неопределенность оценивания значения эталонного образца.

Стандартная неопределенность значения эталонного образца (государственного стандартного образца (ГСО), стандартного образца, аттестованного образца или приготовленного из чистых реактивов) рассчитывается исходя из погрешности аттестации ΔQ.

---

Если образец готовят из стандарт-титра (фиксанала) со строго определенным количеством вещества, то необходимо при оценке неопределенности учесть погрешность содержания вещества и погрешность, вносимую при разбавлении (см. пример 2).

Если образец готовят из чистых реактивов, то необходимо учесть чистоту реактива, погрешность взвешивания, а также погрешность объема, вносимую при его растворении (см. примеры 1–3).

ПРИМЕР 4. Необходимо рассчитать стандартную неопределенность стандартного образца состава водного раствора этанола с номинальным значением массовой концентрации этанола 2 мг/см³ (ГСО 7969–2001), который имеет границы относительной погрешности 1% (при P = 0,95). Стандартную неопределенность u(Q) рассчитывают исходя из нормального закона распределения (так как известны границы погрешности и доверительная вероятность Р):


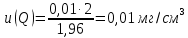
5) Неопределенность оценивания градуировочной функции.

Часто в аналитических измерениях концентрацию вещества находят используя градуировочный график. Для этого из стандартных образцов или чистых реактивов готовят градуировочные растворы с известной концентрацией анализируемого соединения (x_i) и измеряют их аналитический сигнал (y_i).

На основании результатов измерений (y_i) градуировочных растворов и значений концентрации соединений в растворах (x_i) строят градуировочный график, откладывая по оси абсцисс концентрацию соединения в градуировочных растворах х_i, а по оси ординат – соответствующее измеренное значение отклика y_i.

Уравнение градуировочной характеристики обычно имеет линейный вид:

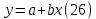
где a – точка пересечения градуировочного графика с осью ординат; b – угловой коэффициент линейного градуировочного графика.

Коэффициенты a и b находят методом наименьших квадратов (МНК). Удобнее всего для этого использовать программу Excel и её функцию ЛИНЕЙН. Для этого необходимо заполнить столбцы значениями x и средних значений y. Затем выделить две смежных ячейки и в строке формул ввести следующую формулу: =ЛИНЕЙН(B1:B5;A1:A5) и нажать «Crtl + Shift + Enter». В ней B1:B5 – это диапазон значений y, A1:A5 – диапазон значений x. В первой выделенной ячейке будет рассчитанное значение

---