Файл: Руководство по выражению неопределенности измерения гост р исо 110952007 Статистические методы. Линейная калибровка с использованием образцов сравнения.docx

где m – масса NaOH, г; P – степень чистоты NaOH; M_r – молярная масса NaOH, г/моль; V – объем раствора NaOH, л.

Стандартная неопределенность концентрации раствора NaOH включает в себя пять вкладов:

u(m) – стандартная неопределенность массы NaOH;

u(V) – стандартная неопределенность объема, в котором был растворен NaOH;

u(P) – стандартная неопределенность степени чистоты NaOH;

u(M_r) – стандартная неопределенность молярной массы NaOH (имеет незначительный вклад и поэтому неучитывается);

u(δ) – стандартная неопределенность повторяемости.

Расчет стандартных неопределенностей u(m), u(V), u(P), u(δ) проводится в соответствии с примерами 1–3, 8.

Суммирование стандартных неопределенностей осуществляется с учетом коэффициентов чувствительности, которые рассчитываются как частные производные выходной величины от входной:







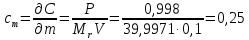
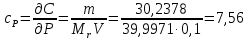
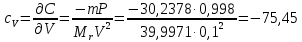
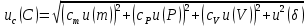
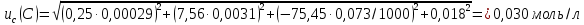
где 0,073/1000 неопределённость объёма переведённая из размерности [мл] в размерность [л].

Расширенная неопределённость при коэффициенте охвата k= 2 и уровнем доверия 0,95:

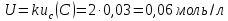
Таким образом, концентрация гидроксида натрия в приготовленном растворе составляет:

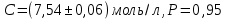
Процентный вклад каждой входной величины в суммарную неопределенность рассчитывается как

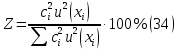
Величина	u(xi)	ci	(ciu(xi))2	Z
m масса	0,00029	0,25	5,256E-09	0,00058
P чистота	0,0031	7,56	0,0005492	60,785
V объём	0,000073	-75,45	3,034E-05	3,35733
δ повторяемость	0,018	1	0,000324	35,8571
∑(ciu(xi))2=			0,000903588

---

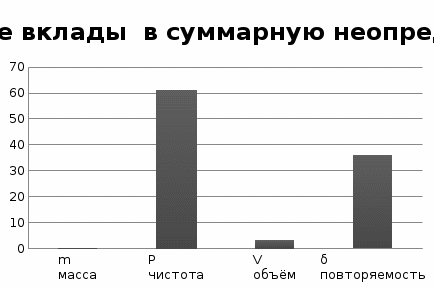
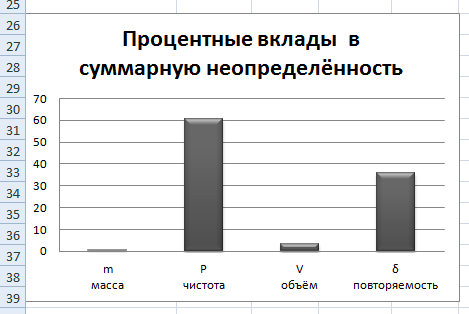
Как видно из гистограммы, наибольший вклад вносит неопределенность, возникающая из-за погрешности объема и случайных факторов.

Бюджет неопределенности, в котором отражается основная информация о рассчитанных неопределенностях, представлен в таблице ниже.

Наимено-вание величины	Значение величины	Тип неопред.	Вид распределения	Станд. неопр. u(xi)	Коэф. чувствите-льности	Проц. вклад Z, %
m, масса навески	30,2378	B	прямоугольное	0,003	0,25	0,00058
P, степень чистоты NaOH	0,998	B	нормальное	0,0031	7,56	60,785
V, объём раствора	0,1	B	треугольное/ прямоугольное	0,000073	-75,45	3,35733
δ, повторяе-мость	7,54	A	нормальное	0,018	1	35,8571

3. Нахождение неопределённости, используя метод Монте-Карло.

Воспользуемся методом статистического моделирования Монте-Карло для оценки неопределённость концентрации раствора гидроксида натрия из примера 9.

ПРИМЕР 10. Исходные данные для моделирования следующие:

- расчётная формула

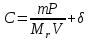
- масса навески гидроксида натрия m=30,2378 г, погрешность взвешивания Δm = ±0,0005 г с прямоугольным распределением;

- степень чистоты гидроксида натрия P=0,998, стандартная неопределённость u(P)=0,0031 с нормальным распределением;

- молярная масса гидроксида натрия M_r=39,9971 г/моль;

- объём раствора V=0,1 л, погрешность определения объёма состоит из двух составляющих: ΔV_k=0,0001 л с треугольным распределением и ΔV_t=0,000105 л с прямоугольным распределением;

- неопределённость связанная со случайными факторами u(δ)=0,018 моль/л.

Для характеристики точности взвешивания и измерения объёма взяты характеристики погрешности (полуширины распределения). Это влияет лишь на используемые формулы для генерации массива случайных значений.

---

В программе Excel сгенерируем массив из 100000 случайных значений для каждой переменной. Общий вид формул Excel приведен в разделе 5.3.2, для нашего примера они примут следующий вид:

Наименование величины	Формула Excel
m	=30,2378+2*0,0005*(СЛЧИС()-0,5)
P	=НОРМОБР(СЛЧИС(); 0,998; 0,0031)
V	=0,1+0,0001*(СЛЧИС()-СЛЧИС())+2*0,000105*(СЛЧИС()-0,5)
δ	=НОРМОБР(СЛЧИС(); 0; 0,018)

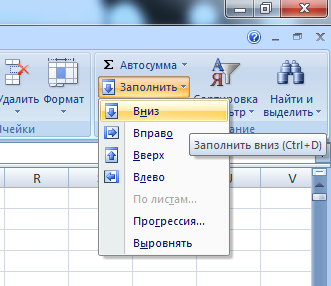
Создадим файл Excel и заполним ячейки A1, B1, C1, D1 приведёнными формулами. Перейдём на ячейку A100000, затем зажав клавишу «Shift» перейдём на ячейку D1 (произойдёт выделение таблицы из 4 столбцов и 100000 строк). На Главной вкладке в разделе Редактирование выберем Заполнить → Вниз.

Полученный массив данных скопируем, нажав клавиши «Ctrl+C».

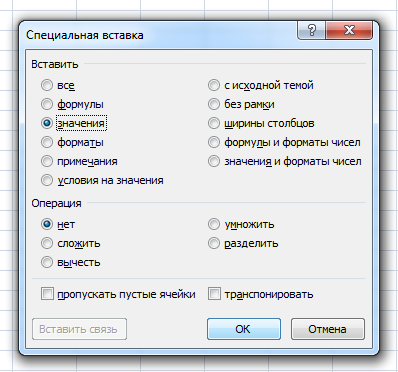
Создадим новый файл Excel, щёлкнем правой кнопкой мыши по ячейке A1, в появившемся контекстном меню выберем Специальная вставка → Значения.

Тем самым мы перенесли сгенерированный массив данных в новый лист Excel. Файл с генерацией случайных значений больше не нужен.

В ячейку E1 введём следующую формулу: =A1*B1/(39,9971*C1)+D1. Заполним ячейки E1:E100000, по аналогии как это было сделано для генерации массива случайных значений.

Скопируем столбец E в столбец D, используя специальную вставку значений.

Отсортируем значения в столбце D от меньшего к большему. Для этого выделим столбец D и на Главной вкладке в разделе Редактирование выберем Сортировка и фильтр → Сортировка от минимального к максимальному.

В свободном месте таблицы введём следующие формулы:

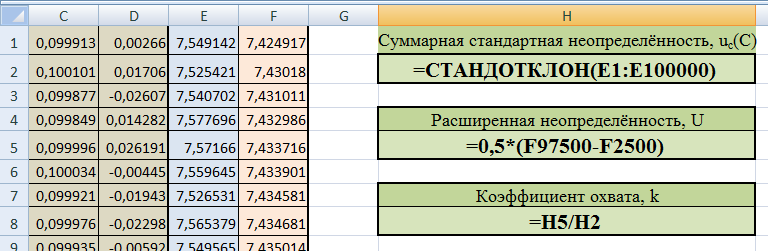
Получаем расширенную неопределённость с уровнем доверия 0,95:

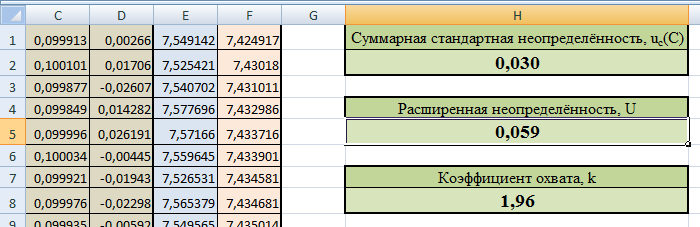
Оценка неопределенности, найденная ММК, совпадает с оценкой неопределённости полученной аналитическим методом.

---

Примечание. Вместо сортировки значений от меньшего к большему и выборкой значений соответствующих границам 97,5% и 2,5% всех значений (ячейки F97500 и F2500), можно использовать функцию Excel ПЕРСЕНТИЛЬ. Тогда формулу для расчёта расширенной неопределённости можно записать в следующем виде: =(ПЕРСЕНТИЛЬ(E1:E100000; 0,975) - ПЕРСЕНТИЛЬ(E1:E100000; 0,025))/2 .

4. Нахождение неопределённости методом частных приращений.

В программе Excel можно реализовать непосредственное вычисление вкладов неопределённости, без определения коэффициентов чувствительности.

Вклад отдельных составляющих вычисляется по формуле (23):

Оценим неопределённость концентрации раствора гидроксида натрия из примера 9.

ПРИМЕР 11. Исходные данные для расчёта следующие:

- расчётная формула

- масса навески гидроксида натрия m=30,2378 г, стандартная неопределенность u(m)=0,00029 г;

- степень чистоты гидроксида натрия P=0,998, стандартная неопределённость u(P)=0,0031;

- молярная масса гидроксида натрия M_r=39,9971 г/моль;

- объём раствора V=0,1 л, стандартная неопределенность u(V)=0,000073 л;

- неопределённость, связанная со случайными факторами u(δ)=0,018 моль/л.

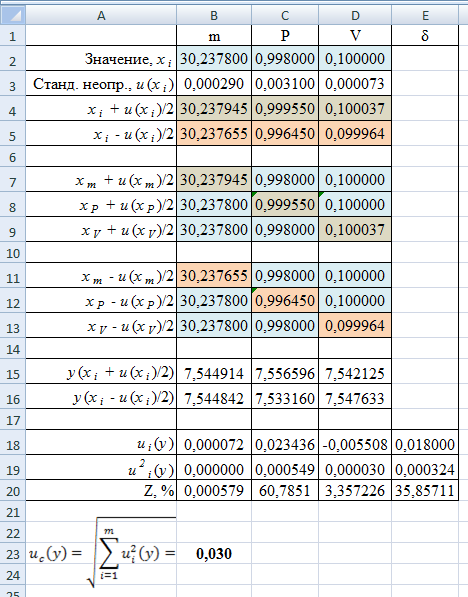
Заполним таблицу исходными данными и формулами, как показано ниже

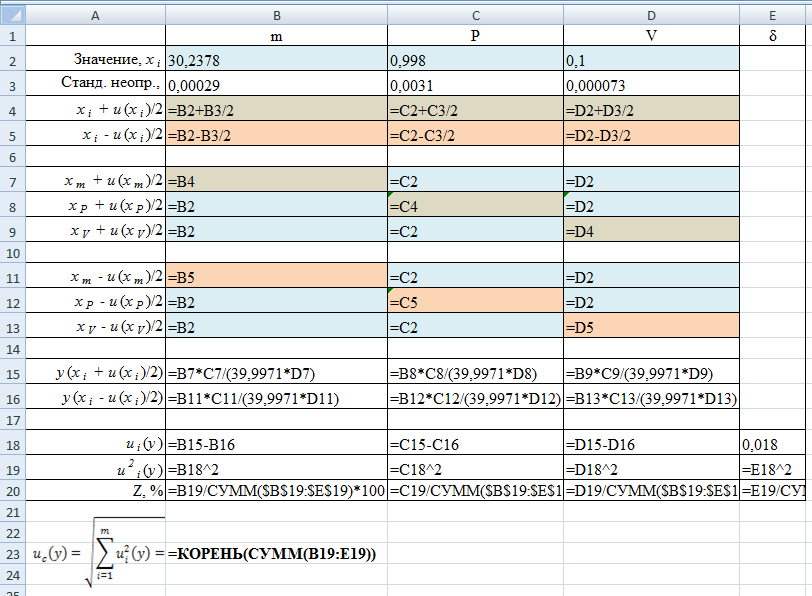
В строках 4 и 5 вычисляются значения переменных скорректированных на половинное значение их неопределённостей (неопределённость, делённая на два, прибавляется или вычитается). В строках 7-9 и 11-13 заполняется матрица значений, где по диагонали представлены скорректированные значения переменных, а в остальных ячейках – исходные значения. В строках 15 и 16 вычисляем концентрацию гидроксида натрия для каждой скорректированной переменной. В строке 18 попарно вычитаем полученные концентрации, тем самым находя вклад каждой переменной в стандартную неопределённость концентрации гидроксида натрия. Извлекая квадратный корень из суммы квадратов всех составляющих неопределённости, получим стандартную неопределённость концентрации гидроксида натрия.

Процентный вклад каждой входной величины в суммарную неопределенность рассчитывается в строке 20.

---

Расширенная неопределённость при коэффициенте охвата k= 2 и уровнем доверия P=0,95 составит:

5. Представление неопределенности, зависящей от результата измерений.

Оценим характер зависимости неопределённости от содержания аналита и установим её для широкого диапазона входных значений, на основе примера 10.

ПРИМЕР 12. Исходная задача как в примере 10, за исключением массы навески гидроксида натрия, которая варьируется в диапазоне от 25 до 50 г.

Найдём расширенную неопределённость для различных навесок гидроксида натрия, полученные данные сведём в таблицу и построим график зависимости неопределённости от концентрации гидроксида натрия.

Масса навески, г	Концентрация NaOH, моль/л	Расширенная неопределённость, моль/л
25	6,24	0,053
30	7,49	0,059
35	8,73	0,065
40	9,98	0,072
45	11,23	0,079
50	12,48	0,086

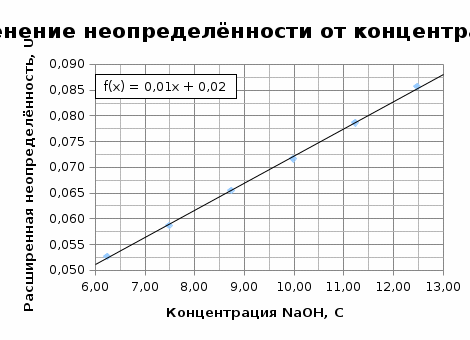
Регрессионное уравнение у = 0,0053x+ 0,0193 отражает зависимость расширенной неопределённости от значения концентрации гидроксида натрия в диапазоне концентраций от 6,25 до 12,5 моль/л.

Таким образом, расширенная неопределённость с уровнем доверия Р=0,95, в диапазоне концентраций от 6,25 до 12,5 моль/л составит:


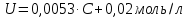
где C – концентрация гидроксида натрия, моль/л.

---