Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 161
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
U=U; 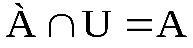 ;
;
 Ø=A;
Ø=A; 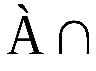 Ø= Ø;
Ø= Ø;
8.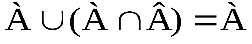 ;
;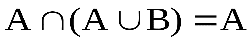
9. Закон инволюции:=
10. Закон исключения разности: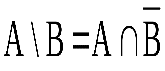 .
.
18. Булеан множеств. Количество элементов булеана конечного множества (с доказательством).
Булеаном множества X называется множество всех подмножеств множества X, включая его само и пустое множество.
Булеан конечного множества конечен, причем количество элементов булеана 2A равно 2n, где n – количество элементов множества A.
Теорема о мощности булеана.Пусть A - конечное множество мощности n , тогда мощность его булеана равна 2n : |Б(A)| = 2n .
Доказательство. Установим соответствие между множествами Б(A)и En по правилу: подмножеству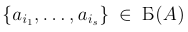 поставим в соответствие набор длины n из нулей и единиц, в котором на местах с номерами i1, . . . , is стоят единицы, а на остальных местах нули. Это соответствие является взаимооднозначным, поэтому |Б(A)| = |En| = 2n . Теорема доказана.
поставим в соответствие набор длины n из нулей и единиц, в котором на местах с номерами i1, . . . , is стоят единицы, а на остальных местах нули. Это соответствие является взаимооднозначным, поэтому |Б(A)| = |En| = 2n . Теорема доказана.
В качестве примера приведенного в доказательстве теоремы соответствия рассмотрим случай n = 3 . Пусть A = {α, β, γ}, тогда
Б(A) = {ø, {α}, {β}, {γ}, {α, β}, {α, γ}, {β, γ}, {α, β, γ}};
E3 = (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1, 0, 1), (0, 1, 1), (1, 1, 1) .
Соответствие между E3 и Б(A) может быть установлено 8! различными способами (оно равно числу перестановок из элементов множества E3 ). В данном случае элементы множества E3 записаны так, что эле- менту, стоящему на k -ом месте, в Б(A) соответствует k -ый элемент множества
в Б(A) соответствует k -ый элемент множества  соответствует (0, 0, 1) , {α, β} — (1, 1, 0) и т. д.
соответствует (0, 0, 1) , {α, β} — (1, 1, 0) и т. д.
Отметим следующее свойство булеана:
Б(A∪B) = {A1 ∪B1|A1 ∈ Б(A), B1 ∈ Б(B)}.
Действительно, пусть произвольное множество C∈ Б(A∪B) , т. е. C⊆A∪B . Обозначим через
A1 = C ∩ A , B1 = C ∩ B . Тогда A1 ⊆A , B1 ⊆B и C = A1 ∪B1 , где A1 ∈ Б(A) , B1 ∈ Б(B) . Докажем обратное включение. Если A1 ∈ Б(A) , B1 ∈ Б(B) , тоA1 ⊆A ,B1 ⊆B . ТогдаA1 ∪B1 ⊆A∪B⇒A1 ∪B1 ∈ Б(A∪B) .
19. Декартово произведение двух и нескольких множеств. Кортежи. Арифметическое n-мерное точечное пространство.
Понятие кортежа, как и понятие множества, является одним из основных математических понятий, поэтому для него также не существует определения через другие понятия. Интуитивно кортеж можно определить какупорядоченныйнабор компонентов. Кортежи одинаковы (равны), если они состоят из одних и тех же компонентов, причем порядок этих компонентов также одинаков.
Компоненты кортежей обычно перечисляются в круглых скобках.
Например,a= (3, 8, 2) – кортеж. Числа 3, 8, 2 – его компоненты. Другой пример кортежа –c= (8, 2, 3). Кортежиaиc– разные.
В кортеже могут быть одинаковые элементы. Например,x= (8, 3, 2, 3) иy= (3, 8, 2, 3) – кортежи, причем разные.
Количество компонентов в кортеже называется его длиной. Например, длина кортежейaиcравна трем, а кортежейxиy– четырем. Кортежи из двух компонентов называют парами, из трех – тройками, и т.д.
Простейший пример кортежа – вектор, задающий координаты точки на плоскости или в пространстве. Очевидно, что, например, точки на плоскости с координатами (5, 7) и (7, 5) – разные.
Как и для множеств, компоненты кортежей могут быть любыми (не только числами). Например, перечень студентов учебной группы, упорядоченный по их среднему баллу за время учебы, можно считать кортежем.
Декартовым (или прямым) произведением множествAиBназывается множество, состоящее из всех тех и только тех пар (т.е. кортежей длины 2), первый компонент которых принадлежит множествуA, а второй – множествуB. Декартово произведение множествAиBобозначается какA×B.
Аналогично определяется произведение трех, четырех и т.д. множеств. Декартово произведение множеств
А1,А2, ...,Аr– это множество всех тех и только тех кортежей длиныr, первый компонент которых принадлежит множествуА1, второй – множествуА2, ...,r-й – множествуАr. Такое декартово произведение обозначается как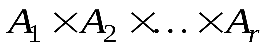 .
.
Декартово произведение множества на само это множество называется декартовым квадратом. Аналогично можно говорить о декартовой третьей степени и т.д.
n-мерным арифметическим пространством называется совокупность всевозможных упорядоченных наборов из n вещественных чисел, над которыми введены две операции:
1) сложение наборов;
2) умножение наборов на вещественные числа.
Операция сложения:
Пусть даны некоторые наборы x = (x1, x2, …, xn ) и y = (y1, y2, …, yn), xiyi – вещественные числа:
x + y = z = (x1 + y1, x2 + y2,…, xn + yn)
Свойства сложения:
x + y = y + x – коммутативность (x + y) + z = x + (y + z) = y + (x + z) – ассоциативность $! (существует единственный) 0 = (0, 0, …, 0) , x + 0 = x "x $!y, что x + y = 0, т. е. y – набор, противоположный x.
Операция умножения на число
x = (x1, x2 … xn), λ Î R
λhx = xhλ = w = (λx1, λx2, … λxn)
Свойства умножения на число:
λhx = xhλ – коммутативность μh(λx) = (μλ)hx 1hx = x 0hx = (0, 0, …, 0).
Совместные свойства операций:
λx + λy = λ(
xy) дистрибутивность μx + λx = (μ + λ )x x + y = 0 Û y = (-1)hx – набор противоположный набору х.
20. Диаграммы Эйлера - Венна основных операций над множествами.
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
21. Теорема об основных свойствах операций над множествами
8.
9. Закон инволюции:=
10. Закон исключения разности:
18. Булеан множеств. Количество элементов булеана конечного множества (с доказательством).
Булеаном множества X называется множество всех подмножеств множества X, включая его само и пустое множество.
Булеан конечного множества конечен, причем количество элементов булеана 2A равно 2n, где n – количество элементов множества A.
Теорема о мощности булеана.Пусть A - конечное множество мощности n , тогда мощность его булеана равна 2n : |Б(A)| = 2n .
Доказательство. Установим соответствие между множествами Б(A)и En по правилу: подмножеству
В качестве примера приведенного в доказательстве теоремы соответствия рассмотрим случай n = 3 . Пусть A = {α, β, γ}, тогда
Б(A) = {ø, {α}, {β}, {γ}, {α, β}, {α, γ}, {β, γ}, {α, β, γ}};
E3 = (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1, 0, 1), (0, 1, 1), (1, 1, 1) .
Соответствие между E3 и Б(A) может быть установлено 8! различными способами (оно равно числу перестановок из элементов множества E3 ). В данном случае элементы множества E3 записаны так, что эле- менту, стоящему на k -ом месте,
Отметим следующее свойство булеана:
Б(A∪B) = {A1 ∪B1|A1 ∈ Б(A), B1 ∈ Б(B)}.
Действительно, пусть произвольное множество C∈ Б(A∪B) , т. е. C⊆A∪B . Обозначим через
A1 = C ∩ A , B1 = C ∩ B . Тогда A1 ⊆A , B1 ⊆B и C = A1 ∪B1 , где A1 ∈ Б(A) , B1 ∈ Б(B) . Докажем обратное включение. Если A1 ∈ Б(A) , B1 ∈ Б(B) , тоA1 ⊆A ,B1 ⊆B . ТогдаA1 ∪B1 ⊆A∪B⇒A1 ∪B1 ∈ Б(A∪B) .
19. Декартово произведение двух и нескольких множеств. Кортежи. Арифметическое n-мерное точечное пространство.
Понятие кортежа, как и понятие множества, является одним из основных математических понятий, поэтому для него также не существует определения через другие понятия. Интуитивно кортеж можно определить какупорядоченныйнабор компонентов. Кортежи одинаковы (равны), если они состоят из одних и тех же компонентов, причем порядок этих компонентов также одинаков.
Компоненты кортежей обычно перечисляются в круглых скобках.
Например,a= (3, 8, 2) – кортеж. Числа 3, 8, 2 – его компоненты. Другой пример кортежа –c= (8, 2, 3). Кортежиaиc– разные.
В кортеже могут быть одинаковые элементы. Например,x= (8, 3, 2, 3) иy= (3, 8, 2, 3) – кортежи, причем разные.
Количество компонентов в кортеже называется его длиной. Например, длина кортежейaиcравна трем, а кортежейxиy– четырем. Кортежи из двух компонентов называют парами, из трех – тройками, и т.д.
Простейший пример кортежа – вектор, задающий координаты точки на плоскости или в пространстве. Очевидно, что, например, точки на плоскости с координатами (5, 7) и (7, 5) – разные.
Как и для множеств, компоненты кортежей могут быть любыми (не только числами). Например, перечень студентов учебной группы, упорядоченный по их среднему баллу за время учебы, можно считать кортежем.
Декартовым (или прямым) произведением множествAиBназывается множество, состоящее из всех тех и только тех пар (т.е. кортежей длины 2), первый компонент которых принадлежит множествуA, а второй – множествуB. Декартово произведение множествAиBобозначается какA×B.
Аналогично определяется произведение трех, четырех и т.д. множеств. Декартово произведение множеств
А1,А2, ...,Аr– это множество всех тех и только тех кортежей длиныr, первый компонент которых принадлежит множествуА1, второй – множествуА2, ...,r-й – множествуАr. Такое декартово произведение обозначается как
Декартово произведение множества на само это множество называется декартовым квадратом. Аналогично можно говорить о декартовой третьей степени и т.д.
n-мерным арифметическим пространством называется совокупность всевозможных упорядоченных наборов из n вещественных чисел, над которыми введены две операции:
1) сложение наборов;
2) умножение наборов на вещественные числа.
Операция сложения:
Пусть даны некоторые наборы x = (x1, x2, …, xn ) и y = (y1, y2, …, yn), xiyi – вещественные числа:
x + y = z = (x1 + y1, x2 + y2,…, xn + yn)
Свойства сложения:
x + y = y + x – коммутативность (x + y) + z = x + (y + z) = y + (x + z) – ассоциативность $! (существует единственный) 0 = (0, 0, …, 0) , x + 0 = x "x $!y, что x + y = 0, т. е. y – набор, противоположный x.
Операция умножения на число
x = (x1, x2 … xn), λ Î R
λhx = xhλ = w = (λx1, λx2, … λxn)
Свойства умножения на число:
λhx = xhλ – коммутативность μh(λx) = (μλ)hx 1hx = x 0hx = (0, 0, …, 0).
Совместные свойства операций:
λx + λy = λ(
xy) дистрибутивность μx + λx = (μ + λ )x x + y = 0 Û y = (-1)hx – набор противоположный набору х.
20. Диаграммы Эйлера - Венна основных операций над множествами.
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
-
В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства. -
Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства. -
В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
21. Теорема об основных свойствах операций над множествами