Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 636

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВОПРОСЫ и ответы К ЭКЗАМЕНУ Комбинаторный признак умножения. Количество битовых строк длины k. Пусть задана последовательность событий E1, E2, E3, …, Em таких, что событие Е1осуществляется n1способами, и если события E1, E2, E3,...,Ек-1осуществились, то событие Ек может осуществиться nкспособами. Тогда существует n1х n2х n3х … х nтспособов осуществления всей последовательности событий.. Битовая строка – это строка, состоящая из элементов множества{0, 1}, т.е. каждый из элементов имеет значение 0 или 1. Сколько существует битовых строк длины 5? Сколько существует битовых строк длины k?Поскольку каждый символ строки может иметь значение 1 или 0, тосуществует два варианта выбора для каждой позиции. Следовательно, существует 2 x 2 x 2 x 2 x 2 = 25 битовых строк длины 5. По аналогичным соображениям, имеется 2k битовых строк длины k. Количество всех подмножеств k - элементного множества. Число всех подмножеств из элементов равно N(M(A))=2^n Комбинаторный признак сложения.  (Комбинаторный принцип сложения) Пусть S1, S 2, S3,... ,Sm – попарно непересекающиеся множества (т.е. SiSj = для всех i  j), и пусть для каждого i, множество Si содержит niэлементов. Количество вариантов вы­бора из S1 или S2или S3 или ... или Smравно n1 + n2 + n3+ … + nm. На языке теории множеств утверждение теоремы имеет вид |S1 S2 S3 ... Sm|= |S1| + |S2| + |S3| + ... + |Sm|, где |S| обозначает количество элементов множества S. Перестановки, размещения, сочетания без повторения. Перестановками -называются наборы состоящие из одного и того элементов,следования элементов. Pn=n!Размещение –называются упорядоченные наборы из элементов выбранных из n элементов, которые отличаются друг от друга, как порядком следования, так и составом элементов. mA =n!/(n-m)!nСочетание- называютсяэлементов выбранных из n элементов, которые отличаются другот друга составом элементов. mС =n!/m!(n-m)!n Бином Ньютона. Треугольник Паскаля. Свойства биномиальных коэффициентов. Формула бинома Ньютонадля натуральныхnимеет вид  , где   -биномиальные коэффициенты, представляющие из себя сочетания изnпоk,k=0,1,2,…,n, а "!" – это знак факториала).К примеру, известная формула сокращенного умножения "квадрат суммы" вида   есть частный случай бинома Ньютона приn=2.Выражение, которое находится в правой части формулы бинома Ньютона, называютразложениемвыражения(a+b)n, а выражение   называют(k+1)-ым членом разложения,k=0,1,2,…,n.Биномиальные коэффициенты для различныхnудобно представлять в виде таблицы, которая называется арифметическийтреугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид: Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральныхn: Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.Для коэффициентов бинома Ньютона справедливы следующие свойства: коэффициенты, равноудаленные от начала и конца разложения, равны между собой  ,p=0,1,2,…,n; ; сумма биномиальных коэффициентов равна числу2, возведенному в степень, равную показателю степени бинома Ньютона:  ; сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. Первые два свойства являются свойствами числа сочетаний. Перестановки, размещения, сочетания с повторениями. Перестановка – _ Размещение- Сочетание- 7. Признак клеток (Дирихле). Принцип Дирихле — простой, интуитивно понятный и часто полезный метод для доказательства утверждений о конечном множестве. Этот принцип часто используется в дискретной математике, где устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий. В английском и некоторых других языках данное утверждение известно как «принцип голубей и ящиков, когда объектами являются голуби, а контейнерами — ящики.Этот принцип утверждает, что если множество из n элементов разбито на m непересекающихся частей, не имеющих общих элементов, гдеn > mто, по крайней мере, в одной части будет более одного элемента.На языке отображений эта формулировка означает, чтоесли в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.Другая формулировка “ принципа Дирихле“:если n + 1 предмет поместить в n мест, то обязательно хотя бы в одном месте окажутся хотя бы двапредмета.В шутливой форме принцип Дирихле выглядит так: “нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев “. [2] Признак математической индукции. Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному. Определение 2 9. Высказывания. Отрицание, конъюнкция, дизъюнкция, их таблицы истинности.Высказываниемназывается повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.Отрицаниемвысказывания  называется высказывание («не », «неверно, что »), которое истинно, когда ложно, и ложно, когда истинно.Таблица истинности для отрицания: Конъюнкцией (логическим умножением) двух высказываний  , называется высказывание (« и »), которое истинно только в том случае, когда и оба истинны.Таблица истинности для конъюнкций: Дизъюнкцией (логическим сложением) двух высказываний  , называется высказывание (« или »), которое истинно, когда хотя бы одно из них истинно.Таблица истинности для дизъюнкций: 10. Импликация и эквиваленция, таблицы их истинности.Импликацией двух высказываний  ,  называется высказывание  («если , то », « влечёт », «из следует », « имплицирует »), которое ложно тогда и только тогда, когда истинно, а ложно.Таблица истинности для импликаций:  Эквивалентностью высказываний  , называется высказывание (« эквивалентно », « тогда и только тогда, когда », «для того, чтобы , необходимо и достаточно, чтобы »), которое истинно тогда и только тогда, когда  и  оба истинны или ложны.Таблица истинности для эквивалентности: 11. Эквивалентные высказывания. Теорема о свойствах логических эквивалентностей.Эквиваленцией (или эквивалентностью) двух высказываний Х, У называется новое высказывание, которое считается истинным, когда оба высказывания Х, У, либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.Эквиваленция высказываний Х, У обозначается символом  (или,

22. Булева алгебра.Булевой алгеброй называется дистрибутивная структура с неравными друг другу единицей 1 и нулем 0, в которой всякий элемент имеет дополнение. Булева алгебра всегда содержит не менее двух элементов. Алгебра, содержащая только 1 и 0, называется вырожденной.23. Основные законы и свойства операций Булевой алгебры.Как любая алгебраическая система булева алгебра базируется на совокупности некоторых предположений, которые принято называть аксиомами, т.е предположениями не требующими доказательств. Аксиомы определяются для двух логических значений 1 ( "ИСТИНА" ) и 0 ( "ЛОЖЬ" ) и операций логического умножения (конъюнкции), которая обозначается " & ", " · " или не обозначается вовсе, логического сложения (дизъюнкции), которая обозначатся " v ", "+", и отрицания ( инверсии ), которая обозначается горизонтальной чертой (" - ") над переменной или выражением, например, . Булевой переменной, обозначаемой обычно xi , называется переменная принимающая два логических значения { 0, 1 }.Ниже приведены аксиомы булевой алгебры относительно дизъюнкции, конъюнкции и отрицания.Аксиомы конъюнкции 0·* 0 = 0 ; 1·* 1 = 1 ; 0·* 1 = 1·* 0 = 0 ;Аксиомы дизъюнкции 0 v 0 = 0 ; 1 v 1 = 1 ; 0 v 1 = 1 v 0 = 1 ;Аксиомы отрицания Если x = 0 , то ˆх = 1 ;Если x = 1 , то ˆх = 0 ;Следующие 5 правил обычно называют теоремами булевой алгебры. Особенностью теорем булевой алгебры является то, что для их доказательства пользуются простой подстановкой значений булевых переменных. Это обусловлено тем, что переменные могут принимать только 2 значения - 0 и 1.Операции с константами : Идемпотентность (тавтология, повторение) :  Для n переменных:  Противоречие :Правило "исключенного третьего" :Двойное отрицание (инволюция) :Следующие 4 правила обычно называют законами или тождествами булевой алгебры.Ассоциативность ( ассоциативный закон ) :   Коммутативность ( коммутативный закон ) :   11. Дистрибутивность ( дистрибутивный закон ) :конъюнкции относительно дизъюнкции: дизъюнкции относительно конъюнкции: 24. Отношения множеств. Область определения и множество значений отношения. Обратное отношение. Область определения отношения R – это подмножество всех элементов х множества Х, для которыхнайдется элемент y, связанный с данным элементом отношением R. Область значения отношения R – подмножество всех элементов y множества У, для которых найдутся элементы x, связанные с y отношением R (). Пример: Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X. Итак, если R — отношение на множестве X, то R X X. Множество всех первых элементов пар из R называется областью определения отношения R. Множеством значений отношения R называется множество всех вторых элементов пар из R. Обратное отношение (отношение, обратное к R) — это двухместное отношение, состоящее из пар элементов (у, х), полученных перестановкой пар элементов (х, у) данного отношения R. Обозначается: R−1. Для данного отношения и обратного ему верно равенство: (R−1)−1= R. Взаимо-обратные отношения(взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого. 25. Специальные свойства отношений на А. Частично упорядоченные множества.Бинарным отношением на множестве А называется подмножество его квадрата RÍ A2. Бинарным отношением между множествами А и В называются подмножество принадлежащее декартовому произведению 2-х множеств: RÍ АхВ.Если упорядоченная пара (а1, а2) принадлежит отношению R, то говорят что а1 R а2, то есть между элементом а1 и а2 уст-но отношение R.Областью определения бинарного отношения называется множество элементов а, в котором в принадлежит бинарному отношению: þR={a|bÎ aRb}.Областью значения бинарного отношения называют множество b, в котором а принадлежит бинарному значению:PR={b|aÎ aRb }.Обратное отношение для отношения R называется отношение: R-1={(b,a)|(a,b) Î R }.Отношение можно задать:-с помощью любого способа задания множеств-С помощью матрицы бинарного отношения. Матрица бинарного отношения это квадратная матрица R элементы которой определяются следующим образом rij=1, (ai,aj)Î R, 0 – в противном случае.-С использованием графа. Каждому бинарному отношению можно подставить в соответствие граф G(X,U), содержащий множество вершин Х, и множество ребер U. При этом вершины ajai соединяются дугой если упорядоченная пара ajai Î R. Так как отношения являются множеством упорядоченных пар, то для отношения можно определить те же операции, что и для множеств (объединение, пересечение, разность, дополнение, симметрическая разность).

Взвешенные графы

Ремарка

Для обозначения номеров строк и столбцов матрицы наборы X и Y индексируются положительными целыми числами: i варьируется от 1 до мощности (размер) X и j варьируется от 1 с числом элементов Y. Подробнее см. запись в индексированных наборах.ЕслиG – граф (ориентированный или нет) без кратных дуг, то его матрица смежностиA являетсябулевой, то есть состоит из нулей и единиц. Для произвольной матрицыX = (xij) с неотрицательными элементами будем обозначать через sign(X) булеву матрицу, полученную изX заменой всех ее положительных элементов единицами. Например,

 
1
2
0
 
1
1
0
 

sign
0
2
1
=
0
1
1
.

3
0
1
1
0
1
Равенство sign(X) =X означает, что матрицаX булева. Легко видеть, чтоsign(X+Y) = sign(sign(X) + sign(Y)),sign(X·Y) = sign(sign(X)·sign(Y))в случае, когдаX иY неотрицательные матрицы, для которых определены соответствующие матричные операции. Далее, если матрицыX иY имеют одинаковую размерность, тоsign(X+Y) = sign(X) sign(Y) (дизъюнкция булевых матриц вычисляется поэлементно).ПустьA иB – булевы матрицы. Матрицу sign(A·B) будем называть ихбулевым произведениеми обозначать черезAB. Всоответствии с определением sign(A·B) =AB. ЕслиA = (aij) иB = (bij), то элементы булева произведенияAB = (cij) определяются формуламиcij = ai1b1j = ai2b2j … ainbnj ,гдеn – число столбцов матрицы
A и число строк ПоложимA[k]= sign(Ak) и будем называть матрицу степенью матрицыA.матрицыB.A[k]булевойЕслиA – матрица смежности графаG, то на месте (i,j) матрицыA[k]находится 1, если на графеG существует путь длиныk изi вj, и 0 в противном случае. Пустьn – число вершин графаG. Тогда матрицаEAA[k]… A[n–1]содержит 1 на месте (i,j) в том и только том случае, когда на графеG имеется хотя бы один путь из вершиныi в вершинуj.33. Мощность. Счетные множества.Определение 1.ПустьN- множество натуральных чисел. Множество S называется счётным множеством, если оно равномощно N, то есть S N.Мощность конечного множества А называется число элементов этого множества.Все счетные множества имеют мощность равную мощности натурального ряда чиселМощность натурального ряда чисел обозначается алеф-нуль.34. Несчетные множества. Несчетность множества действительных чисел R (с доказательством).Несчётное мно́жество — бесконечное множество, не являющееся счётным.

  • не существуетинъективногоотображения� вомножество натуральных чисел� ;

  • �  непустое, и для каждой нумерованной последовательности элементов� существует по крайней мере один элемент� , не входящий в неё;

    • иными словами:� непусто, и не существуетсюръективногоотображения множества натуральных чисел� на� ;

  • мощность� не является ни конечной, ни равнойℵ0 .
Данные определения являются эквивалентными всистеме Цермело— Френкелябез использованияаксиомы выбора. Доказательство эквивалентности данных определений со следующим:

  • мощность �  строго превышает ℵ0
— требует привлечения аксиомы выбора.Надмножество несчётного множества несчётно. Простейший пример несчётного множества—континуум, вопрос о существовании несчётных множеств с мощностью менее мощности континуума составляет содержаниеконтинуум-гипотезы. Теорема 2.Любой отрезок множества действительных чисел состоит из несчетного множества точек.Доказательство:Пусть это не так, тогда все точки отрезка[a, b], a<bможно пронумеровать,[a, b]={x1,x2…}. Выберем отрезок[a1, b1][a, b]не содержащийх1. Таким образом если выбрать отрезок[an, bn]то дальше выберем отрезок[an+1, bn+1]. Продолжая этот процесс получим систему вложенных отрезков[an, bn]такую чтоxnне принадлежит[an, bn], следовательно ни одна точка не принадлежит пересечению   [an, bn]но согласно принципу вложенных отрезков существует точкаξпринадлежащая всем отрезкам. Следовательноξпринадлежит[a, b].Теорема 3.(Кантор).Множество всех действительных чисел несчетно.Доказательство: Если бы множество всех действительных чисел было бы счетно, то было бы счетно любое его подмножество и любой отрезок что противоречит теореме счетности рациональных чисел(Т1) и несчетности любых отрезков(Т2).35. Мажоранты для функций. 36. Оценка числа операций, необходимых для сложения и умножения двух матриц, для вычисления значения многочлена.
алгоритм сложения матриц. Сложение матриц выполняется для каждого / и каждого у. Поскольку / принимает t значений, a j принимает p значений, то выполняется tp операций сложения. Пусть N= max {/и, п). Тогда число выполняемых арифметических операций имеет порядок 0(7V2);алгоритм умножения матрицы Л размера т х р на матрицу В размера р х п. Поскольку к принимает значения от 1 до р, то выполняется р операций сложения и р операций умножения. Величина к изменяется от 1 до р для каждого / и каждого у, поэтому к пробегает значения от 1 до р тп раз. Таким образом, выполняется тпр операций сложения и тпр операций умножения. Следовательно, всего выполняется 2тпр операций. Пусть N = = max{/n, п, р}. Тогда число выполняемых арифметических операций имеет порядок 0(N3);37. Алгоритм сортировки выбором (СВ). Пример. Оценка числа операций. Сортировка выбором — это алгоритм сортировки массивов, в котором на каждой итерации во всей последовательности неотсортированных данных выбирается минимальный элемент (при сортировке по возрастанию) и помещается в первую позицию неотсортированной последовательности. Тем самым готовая (отсортированная) последовательность увеличивается на один элемент, а исходная (неотсортированная) последовательность на один элемент уменьшается.Оценка - сортировка выбором. Рассмотрим число сравнений в процедуре СВ для списка из п элементов. Первый элемент сравнивается с остальными элементами и так далее до ( 1)-го элемента, который сравнивается только с одним элементом. Таким образом, (п 1) + (п 2) + ... + 2 + 1 = я(я 1)/2, так что число сравнений имеет порядок 0(и2);function selectionSort(T[n] a):for i = 0 to n - 2for j = i + 1 to n - 1if a[i] > a[j]swap(a[i], a[j])38. Граф и подграф. Основные понятия.Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов. Подграфом графа G(V,E) называется граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа G(V,E).Определим некоторые операции на графах.
Удаление или добавление ребра.Удаление вершины. Из множества вершин удаляем выбранную вершину, а из множества ребер все инцидентные ей ребра.Стягивание ребра. Отождествляем (стягиваем) вершины инцидентные выбранному ребру.Добавление вершины (разбиение ребра). Выберем некоторое ребро (u,v) из множества ребер и удалим его. В множество вершин добавим новую вершину w, а в множество ребер новые ребра (u,w) и (w,v).39. Орграф, мультиграф, размеченный граф. Основные понятия. Пути, связность. Ориентированный граф (или сокращенно орграф)G = (V,Е) состоит из множества вершинV и множества дугЕ. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представима в виде упорядоченной пары вершин (v,w), где вершинаv называется началом, a w – концом дуги. 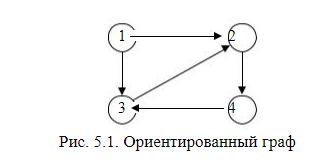Дугу (v,w) часто записывают какv →w и изображают в видеГоворят также, что дугаv →w ведет от вершиныv к вершинеw, а вершинаw смежная с вершинойv.Нарис. 5.1показан орграф с четырьмя вершинами и пятью дугами.Маршрутом длиныиз в в орграфе называется последовательность рёбер видат.е. вторая вершина каждого ребра совпадает с первой вершиной следующего ребра. //Часто удобно представлять маршрут последовательностью вершинкоторые его определяют. Если   , то маршрут называютзамкнутым маршрутомилициклом. 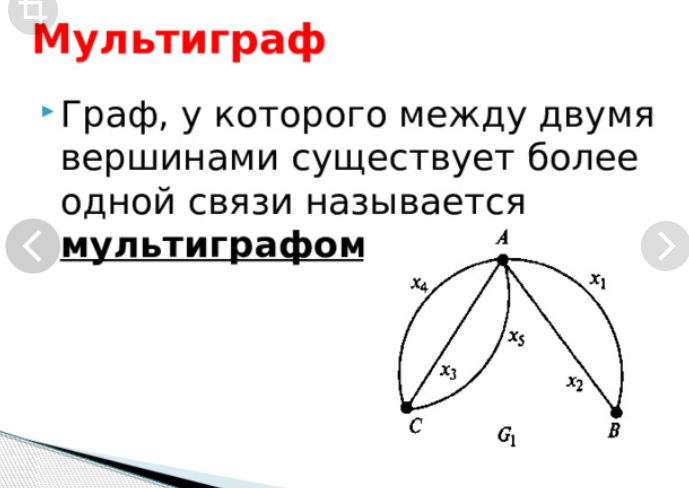Орграф без циклов называютацикличным.Мультиграф — граф, в котором может быть пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений.

Смотрите также файлы