Направление угловой скорости звена АВ определяется следующим образом. Переносим мысленно вектор bа с плана скоростей в точку В шатуна 2 и наблюдаем направление поворота этого звена вокруг точки А.

3.2 Построение планов ускорений механизма

Построение плана ускорений рассмотрим для положения механизма №5 . Так как кривошип ОА вращается с постоянной угловой скоростью, то точка А кривошипа будет иметь только нормальное ускорение, величина которого равна:



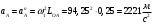
Ползун 3 совершает прямолинейное движение ,ускорение точки В будет равно 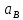и направлено по ОВ.

Векторное уравнение скорости точки В будет иметь вид:



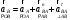
Под векторами указаны их направления.

Для положения 5:



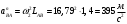
Вводим полюс плана ускорений 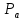.Из полюса откладываем вектор 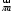в выбранном масштабе и получаем точку «a» из этой точки откладываем вектор 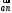(направлен по АВ в сторону точки А). Из точки n проводим вектор 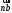(направлен перпендикулярно АВ). Из полюса откладываем направление ускорения 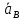и точка пересечения векторов 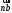и 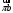дает нам точку пересечения «b». Длина отрезка 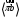дает нам величину ускорения точки В, а длина отрезка 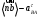. Отмечаем на отрезке 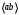середину S₂ и получаем ускорение центра тяжести звена 2.

Примем длину вектора 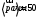. Тогда, масштаб для плана ускорений: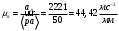



Рассчитаем

---

:



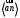
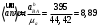
Ускорения нужных точек и звеньев находим по формулам:



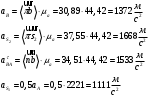
Угловое ускорение звена 2:



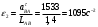
Направлена 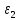по 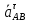из точки В.

Планы ускорений представлены на рисунке 3.3.



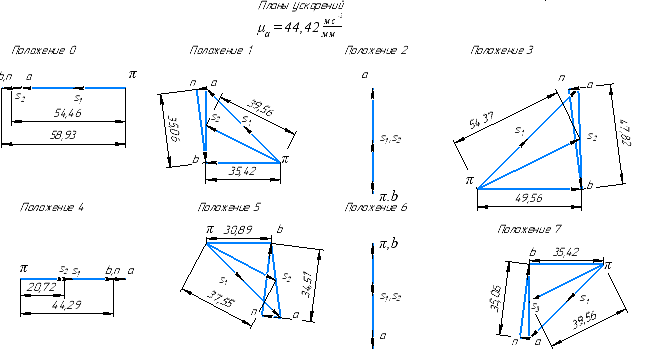
Рис. 3.3 Планы ускорений
Для остальных положений все расчеты и построения ведутся аналогично. Результаты всех построений и расчетов сведены в таблицу:

Таблица 3.1 — Значения ускорений в расчетных положениях

Положение	0	1	2	3	4	5	6	7
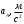	2221	2221	2221	2221	2221	2221	2221	2221
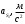	1111	1111	1111	1111	1111	1111	1111	1111
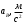	2618	1573	0	2201	1967	1372	0	1573
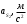	2419	1758	1111	2415	920	1668	1111	1758
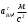	0	1557	2221	2124	0	1533	2221	1557
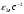	0	1112	1586	1517	0	1095	1586	1112

---

4 Силовой расчет рычажного механизма

4.1 Определение сил и моментов, приложенных к механизму

План нагрузок механизма предусматривает нанесение на его схему векторов сил, действующих в его шарнирах и центрах масс, на основании которых в дальнейшем находится мгновенное значение уравновешивающей силы.

При простейшем кинематическом анализе на план нагрузок наносятся вектора веса звеньев G, внешняя нагрузка Q, уравновешивающая сила F_УР и инерционные нагрузки F_И. Вектора последних направляются противоположно ускорениям центров масс по плану ускорений.

Планы нагрузок представлены в графической части курсовой работы.

Центры тяжести звеньев (стержней)находятся на середины их длины. Центр тяжести ползуна совпадает с центров шарнира В.

Вес звеньев определяется по формуле:



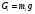
Где 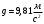– ускорения свободного падения.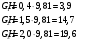



Силы инерции звеньев вычисляются по формуле:



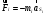
Где 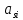-ускорение центра масс i-ого звена.

Знак «-» показывает, что силы инерции направлены противоположно ускорению центра масс звена.

Моменты инерции звеньев относительно их оси вращения:



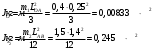
Вычислим силы инерции для 4 положений механизма (5,6,7,0):
Табл. 4.1 — Силы инерции

Положение механизма	5	6	7	0
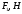	444	444	444	444
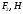	2502	1666	2367	3629
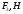	2744	0	3146	5236
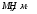	268	389	272	0

---

4.2 Определение уравновешивающей силы методом Жуковского

Соотношение между силами, приложенными к механизму (включая и силы инерции), можно получить с помощью вспомогательного рычага Жуковского.

Если какой-либо механизм под действием системы сил, приложенных к этому механизму, находится в равновесии, то повернутый на 90 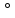в сторону вращения уголовной скорости план скоростей, рассматриваемый как твердое тело, вращающегося вокруг полюса плана и нагруженное теми же силами, приложенными в соответствующих точках плана, также находится в равновесии. При этом, силы, приложенные к полюсу или пересекающие его не указываем, чтобы не загромождать рисунки.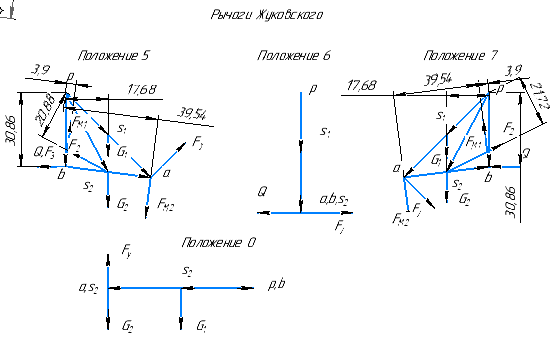



Рис. 4.1. Рычаги Н. Е. Жуковского.

Раскладываем момент инерции звена 2 на пару сил:



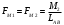
Табл. 4.2 Значение пары сил от момента инерции

Положение механизма	5	6	7	0
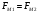	191	278	194	0

Составим уравнения моментов сил относительно полюса .

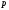Положение 5:



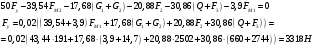
Положение 6:



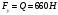
Положение 7:



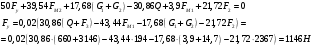
Положение 0:



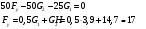
Определяем уравновешивающий момент по формуле



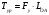
Все вычисления приводим в таблицу 4.4:
Табл.4.4 Полученные результаты

Положение механизма	5	6	7	8
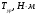	830	165	287	4
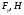	3318	660	1146	17

---

Наибольшую нагрузку по модулю кривошип испытывает в положении 5, поэтому расчет редуктора производим по этому значению.

5 Проектирование эвольвентного зацепления

По найденному максимальному значению уравновешивающей силы, приложенной к кривошипу, определяем вращающийся момент на входном валу привода:

Мощность на валу кривошипа:



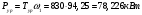
Определим мощность на валу Р_РО:



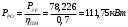
Передаточное отношение редуктора принимаем по рекомендациям для одноступенчатых прямозубых редукторов. Принимаем .

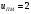Рассчитаем частоту вращения валов редуктора:





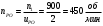
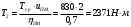
Рассчитываем межосевое расстояние:



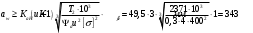
Где 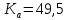—коэффициент межосевого расстояния для цилиндрических зубчатых колес;

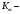коэффициент ширины колес относительно опор;

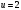– передаточное число;

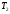– вращающий момента на тихоходном валу редуктора;

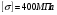− допускаемое контактное напряжение колеса;

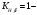коэффициент неравномерности по длине зуба.

По ГОСТ 2185-66 выбираем ближайшее стандартное межосевое расстояние (ряд 1):

Принимаем .

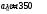Определяем модуль зацепления:



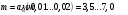
Значение модуля округляется до стандартного числа согласно ГОСТ 9563-60.

Принимаем .

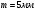Определим суммарное количество зубьев шестерни и колеса:



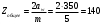
Примем .

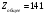Число зубьев шестерни:

---

Смотрите также файлы

• мір ауіпсіздік негіздері.docx

• Лабораторная работа (.docx

• Решение комплексных экономических задач междисциплинарного характера.docx

• Лекции Основы семейного консультирования.docx

• Введение в процессе управления предприятием, бизнесом важное место занимает бизнеспланирование.docx