Файл: Отчет по лабораторной работе 1 по дисциплине Механика жидкости и газа.doc

Процессы в аэродинамической трубе: Описать внутри трубы вентилятор создает вихрь атмосферного воздуха, который частично выравнивается благодаря турбулизатору и решетке. Трубка на выходе имеет сужающееся сопло, поэтому оно является конфузором.Параметры потока: скорость потока постоянна, т. к. режим работы стационарный. Скорость потока вдоль канала возрастает, а статическое давление и плотность уменьшаются. В поперечном сечении статическое давление остается постоянным, а полное давление у стенок меньше, чем по центру трубки из-за наличия потерь на трение в пограничном слое. В результате скорость течения у стенок канала тоже уменьшается.Модель течения: принимается энергоизолированная, несжимаемаемая модель течения. Следовательно, следует пренебречь нагревом воздуха в аэродинамической трубе и повышением полного давления за счёт подвода механической энергии в вентиляторе аэродинамической трубы.На основании этой модели должна быть разработана математическая модель расчёта теоретической зависимости полного и статических давлений от угла скоса потока.

4 ПОРЯДОК ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

1. Проверить схему подключения трубки Пито для раздельного измерения давлений.2. Проверить отсутствие посторонних предметов в рабочей зоне аэродинамической трубы. Визуальным осмотром убедиться в отсутствии повреждений и неисправностей трубы и приёмников давления.3. Записать в протокол измерений дату измерения и показания барометра-анероида (атмосферные давление и температура).4. Включить электропитание установки и запустить аэродинамическую трубу.5. Выждать несколько минут для установления потоков в рабочем помещении.

6. Установить угол скоса потока и снять замеры по левому и правому коленам U-образных жидкостных дифференциальных манометров для полного и статического давлений.7. Повторить измерения для нескольких углов скоса потока от 0 градусов до 90 градусов.8. Для накопления статистики сменить операторов (бригаду студентов) и повторить цикл измерений для тех же гулов скоса потока.9. Выключить аэродинамическую трубу и электропитание установки.

5 РЕЗУЛЬТАТЫ ПРЯМЫХ ИЗМЕРЕНИЙ

5.1 ОСНОВНЫЕ ДАННЫЕ

Измерения осуществлены:– дата измерения – 18.03.22;– атмосферное давление B = 759,9 мм рт.ст;– атмосферная температура t = 31 C.Прямые измерения уровней жидкости в левом и правом коленах U‑образных дифференциальных манометров приведены в приложении А.

5.2 РЕЗУЛЬТАТЫ ПЕРВИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ИЗМЕРЕНИЙ

После проведения измерения давлений нужно получить зависимость давлений от угла скоса – теоретическую и экспериментальную.Полученные экспериментальные значения следует подвергнуть первичной обработке. Ведь проведенные нами измерения являются косвенными – функциями одной или нескольких величин. Поэтому нужно найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных. Учитываются систематические и случайные ошибки. Первым делом следует определить давление невозмущённого потока, то есть атмосферное (перевод из мм рт.ст. в Па):

Па.

(6)

Из уравнения Бернулли можно вывести формулы определения полного и статического давлений:

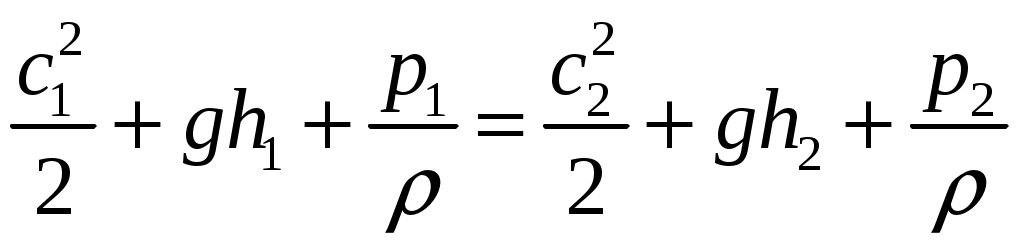(7)

Индекс 1 – величина для полного давления, индекс 2 – величина для статического давления. Учитывая, что :

(8)

где – среднее значение измеренного полного давления, – атмосферное давление. - среднее значение изменения высоты уровня жидкости, которое определяется выражением вида:

(9)

Если принять во внимание значение плотности воды, равное 1 г/ см³, то выражение (3) можно записать следующим образом:

(10)

Для статического давления вывод формулы происходит таким же образом, что и для полного, поэтому итоговое выражение для статического давления принимает вид:

(11)

Результаты расчетов для различных значений угла скоса представлены в Приложении А.Вывод формул для расчета ошибок представлен в Приложении Б.

6 ВТОРИЧНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ

Основная задача вторичной обработки – получить теоретическую зависимость полного и статического давлений от угла скоса потока. Расчёт теоретических значений давлений отличается от формул (10) и (11). Давление частичного торможения рассчитывается по следующей формуле:

(12)

Если учесть зависимость скорости потока от угла скоса и принять, что – атмосферное давление, рассчитанное в выражении (6), то формула (12) принимает вид для полного и статического давлений соответственно:

;	(13.1)
.	(13.2)

6.1 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕОРЕТИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ
К УГЛУ СКОСА ПОТОКА

Для применения формул (13.1) и (13.2) требуется знать неизвестные величины: плотность воздуха и скорость воздушного потока.Нахождения неизвестных величин можно осуществить с помощью уравнения состояния атмосферного воздуха и формулы скорости воздушного потока соответственно (вычисление скорости производится при нулевом угле скоса потока):

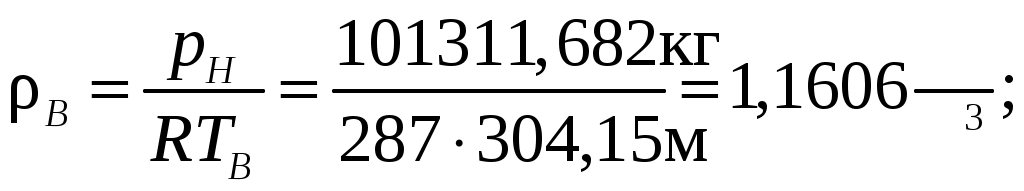	(14)
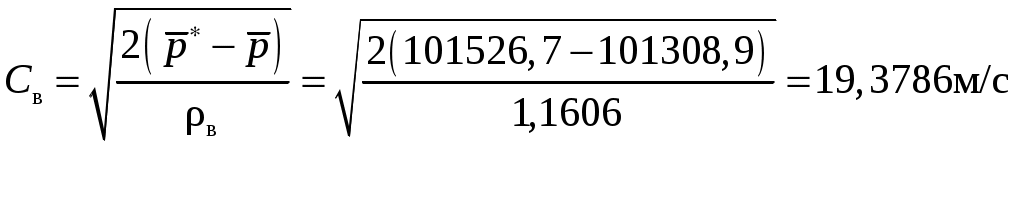.	(15)

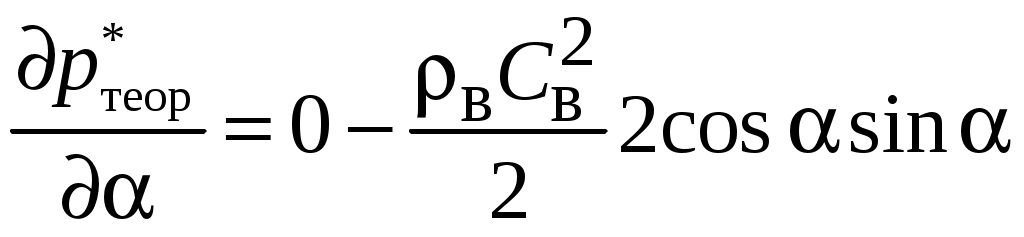Частная производная показывает чувствительность к углу скоса потока. Следовательно, производные по углу скоса от формул (13.1) и (13.2) выглядят следующим образом:

;	(10.1)
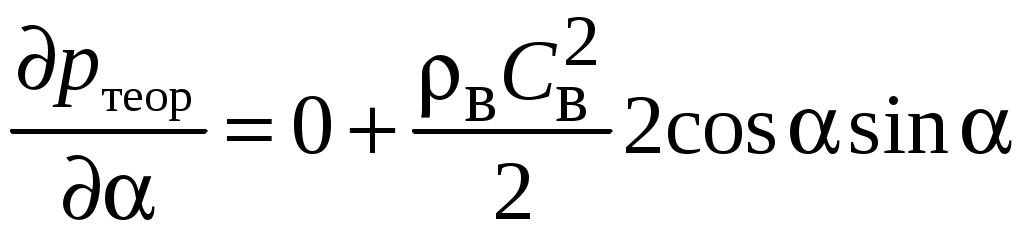.	(10.2)

6.2. РАСЧЁТ ЧУВСТВИТЕЛЬНОСТИ К УГЛУ СКОСА ПОТОКА
И ОШИБОК ДАННОГО РАСЧЁТА

Результат расчета теоретического полного давления и теоретического статического давления для угла скоса :

Па;	(11.1)
Па.	(11.2)

Результат расчета чувствительности к углу скоса :

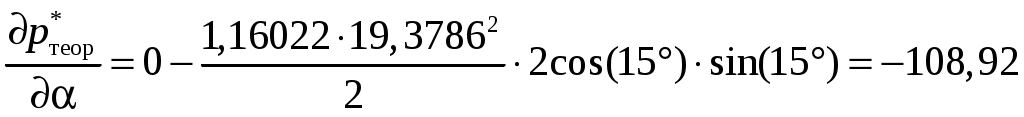;	(10.1)
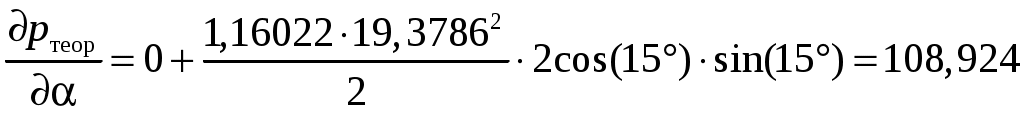.	(10.2)

Результаты расчета для других углов скоса представлены в Таблице 1.Таблица 1 Расчет чувствительности к углу скоса

α, град
0	0	0
15	-108,92	108,924
30	-188,66	188,662
45	-217,85	217,848
60	-188,66	188,662
75	-108,92	108,924
90	-3E-14	2,7E-14

Результаты расчета показывают некоторую закономерность: при приближении угла скоса к 45 градусам значения чувствительности возрастают, а при удалении убывают. С математической точки зрения это объясняется тем, что произведение синуса и косинуса одного угла дают максимальное значение именно при 45 градусах. По таблице видно, что чувствительность при замере