ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 58
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 5 Таблица макроса «НовыйАдрес»
1.3 Остановка записи макросов: после написания в таблицы значения, нажимаем кнопку «Остановить запись» (рис. 6).
Рис. 6 Остановка записи макроса
1.4 Выполнение макросов с помощью заданных сочетаний клавиш: задать для вызова макроса «СтарыйАдрес» сочетание клавиш Сtrl+C (где С - буква латинского алфавита). Для «НовыйАдрес» - Сtrl+H. И эти записи записываем в «Параметре макроса» (рис. 7).
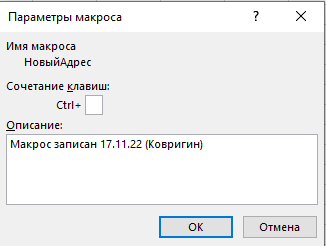
Рис. 7 «Параметры макросов»
1.5 Выполнение макросов: нажать кнопку «Макрос» и «Выполнить» – выполняестя одна из двух макросов (рис. 8).
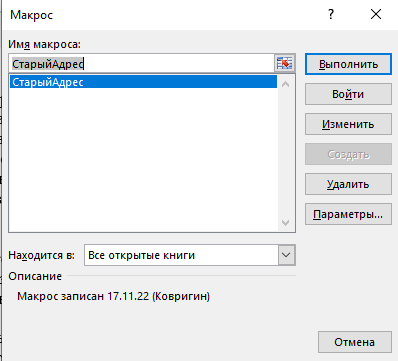
Рис. 8 Выпонение макросов
2. Изменение макросов в VBA и использование процедур ( На рис. 3 нажимаем «Visual Basic»).
2.1 Изменить текст в листе «Модуль 1»: замена номера дома в адресе («3» заменить на «3/5», вручную записываем новый текст) (рис. 9.1 и 9.2) и проеверяем макросы снова.
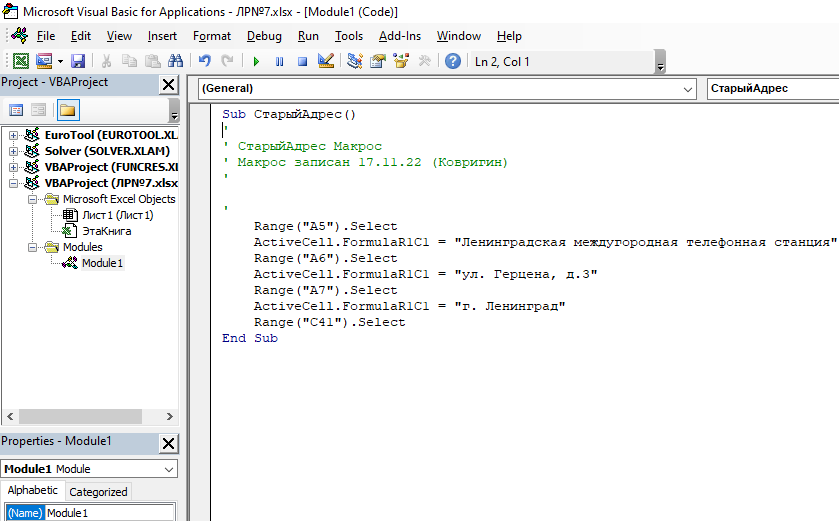
Рис. 9.1 Код программы в VBA до замены номера дома в адресе
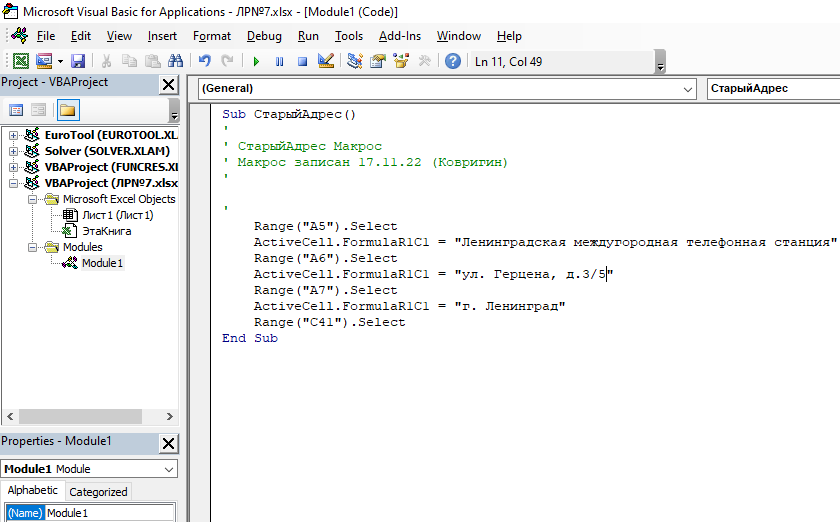
Рис. 9.2 Код программы в VBA после замены номера дома в адресе
2.2 Введение в программный код VВА изменения: Создание новой процедуры, «Formatting» и его команды. Возвращение на лист Ехсеl и выполнить макросов «СтарыйАдрес» и «НовыйАдрес» (рис. 10). Потом изменяем процедуры «Formatting» следующим образом:
• установить размер шрифта 16 пт.;
• установить зеленый цвет шрифта (индекс зеленого цвета - 50);
• установить зачеркнутый шрифт (рис. 11).

Рис. 10 Программный блок схемы «Formatting», «НовыйАдрес» и «НовыйАдрес»
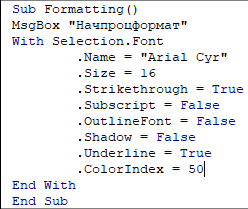
Рис. 11 Изменения процедуры «Formatting»
2.3 Изменения в программной блок схеме: добавляем везде «Formatting» так, как показана на рис. 12., потом возвращаемся на лист Ехсеl и выполняем макросы «СтарыйАдрес» и «НовыйАдрес», после введения команд «Formatting» (рис. 13).
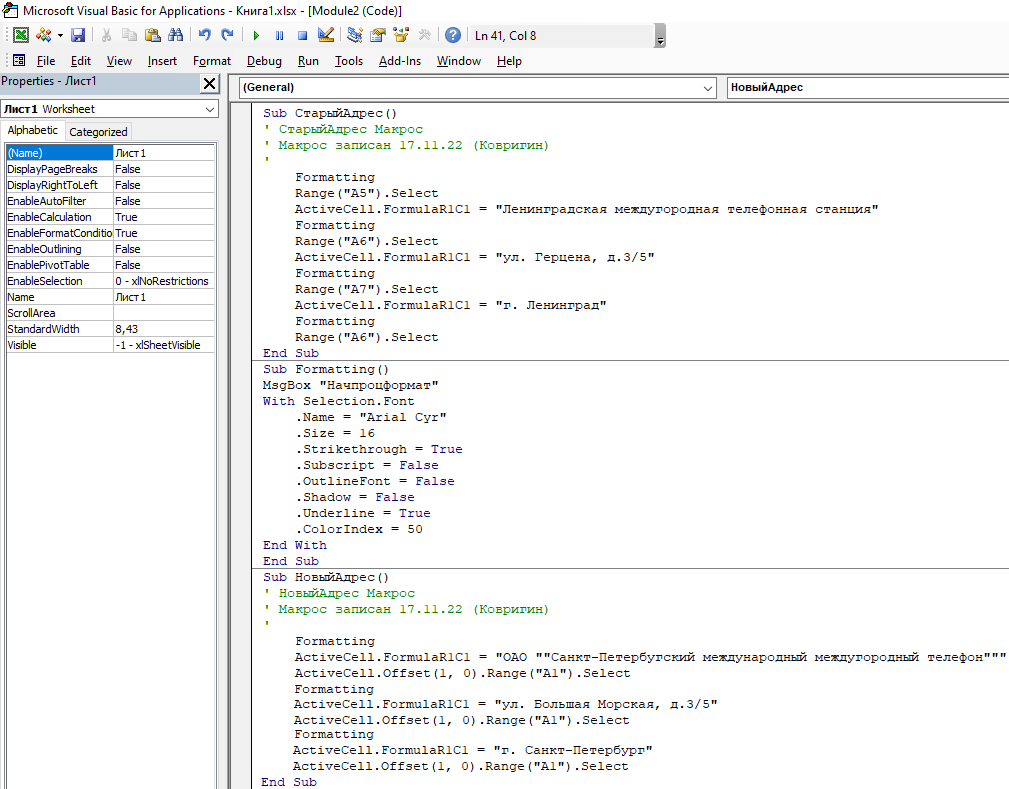
Рис. 12 Изменение в программной блок схеме


Рис. 13 Выполнение программы для макросов: «СтарыйАдрес», «НовыйАдрес»
3. Создание и применение пользовательских Функций (Excel)
3.1 Создание таблицы: Введение Функции «Надбавка», позволяет вычислить размер надбавки в зависимости от количества продаваемого товара (рис. 14).
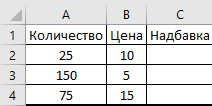
Рис. 14 Таблица Функции «Надбавка»
3.2 Функция «Надбавка» в VBA: На рис. 15 показано как создать лист модуля в VBA; на рис. 16 – Программный код Функции; на рис. 17 – получаемый результат (подставляем значения Функции в ячейки: С2:С4.

Рис. 15 Создание листа модуля в VBA
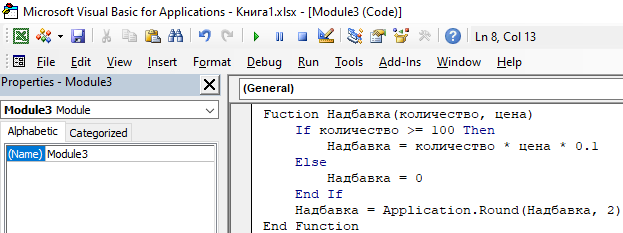
Рис. 16 Программный код Функции «Надбавка»
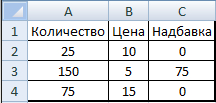
Рис. 17 Результат Функции (Excel и VBA)
4. Назначение макросов объектам в листе.
4.1 Вызовы макросов: на вкладке «Разработчик», нажимаем «Вставить», затем выбираем кнопку для вызова макросов («СтраыйАдрес» и «НовыйАдрес») (рис. 18 – 20).
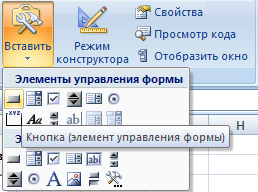
Рис. 18 Первые две кнопки для вызова макросов
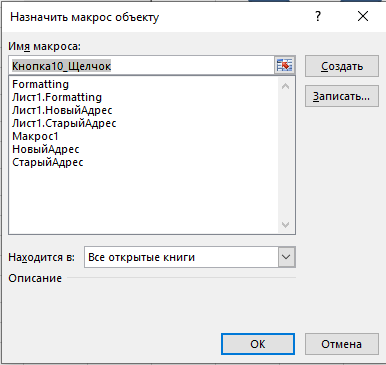
Рис. 19 «Назначения макросов объектам»
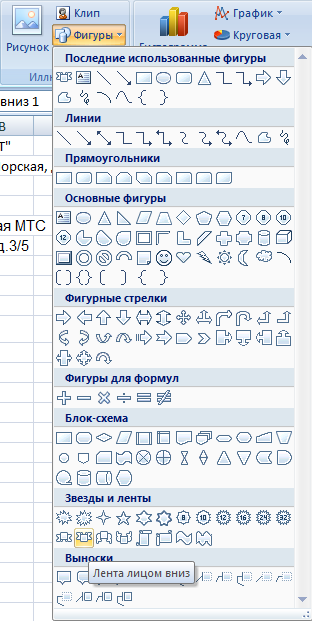
Рис. 20 Вызов макроса («Звезды и ленты».- нажимаем кнопку «Лента лицом вниз» два раза)

Рис. 21 Результаты вызовов макросов (четырёх кнопок)
Лабораторная работа № 10 (8)
Принятие решений в условиях неопределенности. Игры с природой.
Цель работы: освоить и закрепить практические навыки по принятию и обоснованию управленческих решений в условиях недостатка информации, когда одним из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы».
Задание на выполнение работы: Решите задачу, согласно вашему индивидуальному варианту.Определите оптимальную стратегию используя критерии Вальда, Сэвиджа и Гурвица.
Порядок выполнения работы:
Краткие теоретические сведения
Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игрок1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально.
Матрица игры с природой А = ||аij||, где аij – выигрыш (потеря) игрока 1 при реализации его чистой стратегии i и чистой стратегии j игрока 2 (i=1, …, m; j=1,…,n).
Мажорирование стратегий в игре с природой имеет определенную специфику: исключать из рассмотрения можно лишь доминируемые стратегии игрока 1: если для всех g=1,…, n akj alj, k, l = 1,…,m, то k-ю стратегию принимающего решения игрока 1 можно не рассматривать и вычеркнуть из матрицы игры. Столбцы, отвечающие стратегиям природы, вычеркивать из матрицы игры (исключать из рассмотрения) недопустимо, поскольку природа не стремится к выигрышу в игре с человеком, для нее нет целенаправленно выигрышных или проигрышных стратегий, она действует неосознанно.
Рассмотрим организацию и аналитическое представление игры с природой. Пусть игрок 1 имеет m возможных стратегий: А1,А2, … , Аm, а у природы имеется n возможных состояний (стратегий): П1, П2, ..., Пn, тогда условия игры с природой задаются матрицей А выигрышей (потерь) игрока 1:

Возможен и другой способ задания матрицы игры с природой: не в виде матрицы выигрышей (потерь), а в виде так называемой матрицы рисков R = ||rij||m,n. Величина риска - это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей (потерь) А.
Риск - это разность между результатом, который игрок мог бы получить, если бы он знал действительное состоянием среды и результатом, который игрок получит при j-ой стратегии.
Зная состояние природы (стратегию) Пj, игрок выбирает ту стратегию, при которой его выигрыш максимальный или потеря минимальна, т.е.
rij = j-aij, где j = max aij, при заданном j. 1 i m если аij - выигрыш
rij = aij - j, где j = min aij, при заданном j. 1 i m если аij – потери (затраты)
Неопределенность, связанную с полным отсутствием информации о вероятностях состояний среды (природы), называют «безнадежной».
В таких случаях для определения наилучших решений используются следующие критерии: Вальда, Сэвиджа, Гурвица.
Критерий Вальда. С позиций данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник.
Если в исходной матрице по условию задачи результат aij представляет выигрыш лица, принимающего решение, то выбирается решение, для которого достигается значение W = max min aij, 1 i m, 1 j n – максиминный критерий.
Если в исходной матрице по условию задачи результат aij представляет потери лица, принимающего решение, то выбирается решение, для которого достигается значение W = min max aij, 1 i m, 1 j n – минимаксный критерий.
В соответствии с критерием Вальда из всех самых неудачных результатов выбирается лучшей. Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай.
Критерий минимаксного риска Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей А, а матрицей рисков R:
S = min max rij 1 i m, 1 j n.
Применение критерия Сэвиджа позволяет любыми путями избежать большого риска при выборе стратегии, а значит, избежать большего проигрыша (потерь).
Критерий пессимизма-оптимизма Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом.
Критерий основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятность (1-р) и в самом выгодном состоянии с вероятностью р, где р – коэффициент пессимизма.
Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением:
HA = max p max aij + (1-p) min aij , 1 i m, 1 j n. если aij – выигрыш
HA = min p min aij + (1-p) max aij , 1 i m, 1 j n. если aij – потери (затраты)
При p = 0 критерий Гурвица совпадает с критерием Вальда. При p = 1 приходим к решающему правилу вида max max aij, к так называемой стратегии «здорового оптимизма», критерий максимакса.
Применительно к матрице рисков R критерий пессимизма-оптимизма Гурвица имеет вид: