Файл: Контрольная работа по дисциплине Математика ИнститутФакультетДепартамент Студент.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 101

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждениевысшего образования«Уральский государственный экономический университет»КОНТРОЛЬНАЯ РАБОТАпо дисциплине «Математика»

Институт/Факультет/Департамент/



Студент

Центр




Притчин А.П.

Институт непрерывного образования



(ФИО)







Группа


ИДО ОЗБ УП-22 Шад

Направление (Специальность)






Управление персоналом



Руководитель







Кныш А.А.

















































Екатеринбург2023 г1. Вычислить пределы.
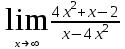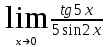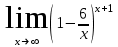
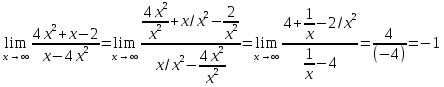
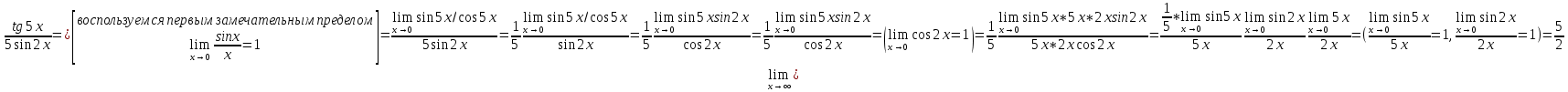
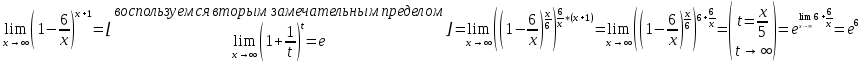
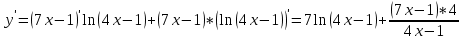
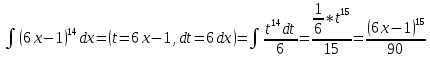
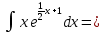
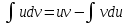
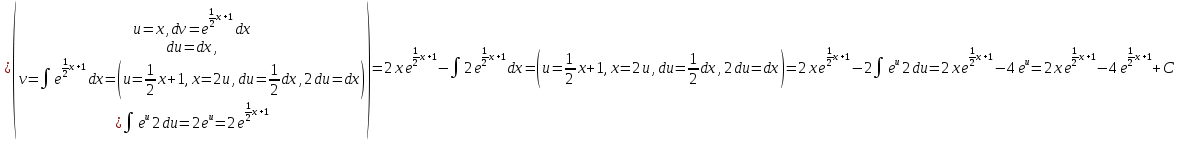
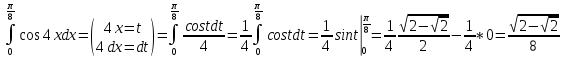
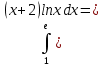
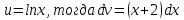
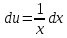
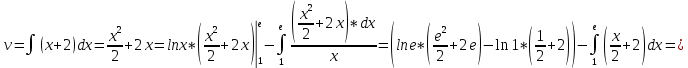
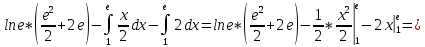
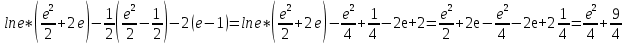
Вариант 6. а) б) в)А) Б)В)2. Найти первую производную функции Вариант 6. y=(7x-1)ln(4x-1)3. Найти неопределенный интеграл: Вариант 6. а)б)в) А) Б) Интегрируем «по частям»4. Вычислить определенный интеграл:Вариант 6. а) ; б) .А) Б) Интегрируем «по частям»Пусть ==5. Решить систему уравнений:
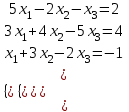
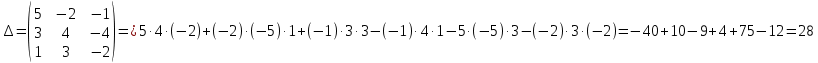
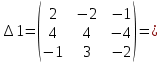
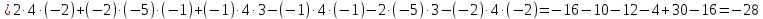
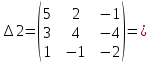
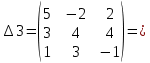
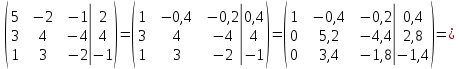
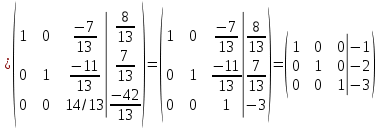
а) методом Крамера,б) методом ГауссаВариант 6. А) Методом Крамера= 5·4·(-2) + 2·(-5)·1 + (-1)·3·(-1) - (-1)·4·1 - 5·(-5)·(-1) - 2·3·(-2) = -40 - 10 + 3 + 4 - 25 + 12 = -56= 5·4·(-1) + (-2)·4·1 + 2·3·3 - 2·4·1 - 5·4·3 - (-2)·3·(-1) = -20 - 8 + 18 - 8 - 60 - 6 = -84X1 = -28/28=-1X2=-56/28=-2X3=-84/28=-3Б)X1=-1X2=-2X3=-36.По координатам вершин треугольника ABC найти:

  1. периметр треугольника;

  2. уравнения сторон AB и BC; уравнение высоты AD.
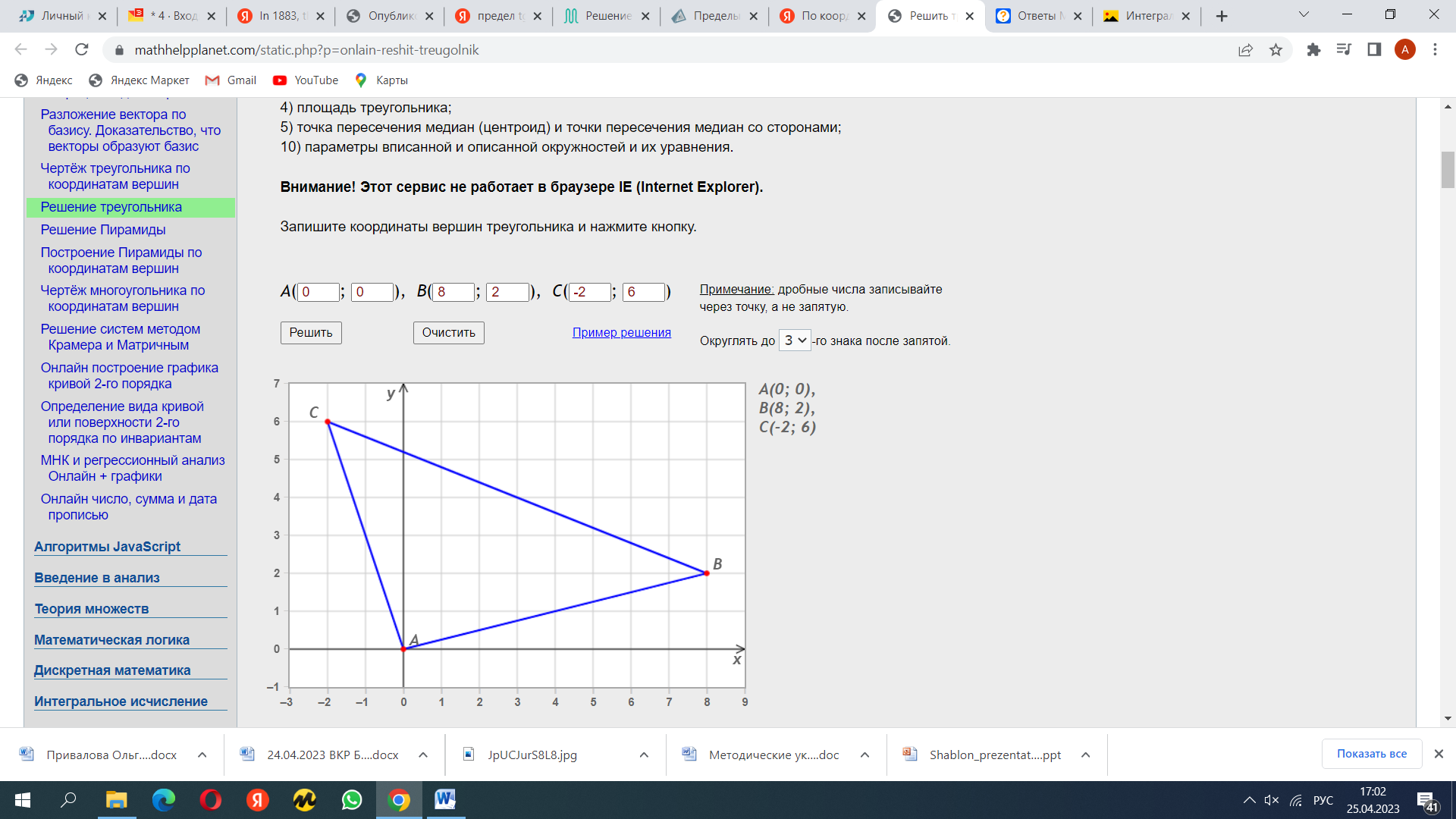
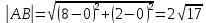
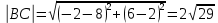
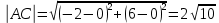
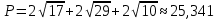
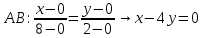
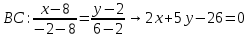
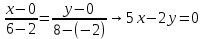
Сделать чертежВариант 6. А(0;0); В(8;2); С(-2;6).Периметр треугольникаУравнение стороны АВУравнение стороны ВСУравнение высоты ADДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА2 семестрТема 1. Элементы комбинаторики. События и их вероятности, классический и геометрический способы подсчета вероятностейВариант 6. Из партии, в которой 30 деталей без дефекта и 5 с дефектом, берут наугад три детали. Какова вероятность того, что среди них ровно две детали без дефекта?
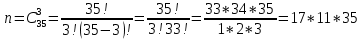
Решение:Событие А= {среди отобранных ровно две детали без дефекта}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 3 детали из партии, т.е. из 35 деталей. Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди 30 деталей ровно 2 детали без дефекта): детали без дефекта можно выбрать из трех 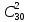способами; при этом оставшаяся делать с дефектом. Выбрать одну деталь с дефектом из 5 с можно 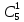способами. 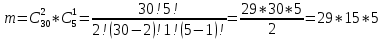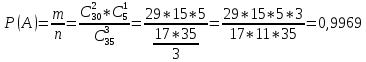Следовательно, Тема 2.Операции над событиями. Правила сложения и умножения вероятностейВариант 6. В сессию студент должен сдать 4 экзамена. Вероятность не выдержать первый – 0,1, для последующих экзаменов – 0,2; 0,15; 0,25 соответственно. Какова вероятность того, что студент сдаст хотя бы один экзамен?Решение:Пусть событие 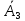= {студент сдал первый экзамен}, = {студент не сдал первый экзамен}, ={ студент сдал второй экзамен }, ={ студент не сдал второй экзамен }, ={ студент сдал третий экзамена}. ={ студент не сдал третий экзамена}. 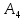={ студент сдал четвертый экзамена}. 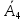={ студент не сдал четвертый экзамена}.События и

– противоположные, поэтому ,



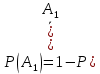
. Аналогично







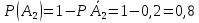
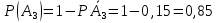
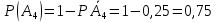
Событие В ={ студент сдал хотя б один экзамен}. Это означает, что был дан ответ на любой один вопрос, или на любые два вопроса, или на все три вопроса. Событие = {студент не сдал ни один экзамен}. События B и противоположны, поэтому . Событие означает, что одновременно появились независимые события , и , т. е. . По правилу умножения вероятностей для независимых событий 0,1*0,2*0,15*0,25=0,00075.

Итак, Р(В)=1-0,00075=0,99925.
Тема 3. Формула полной вероятности. Формулы Бейеса
Вариант 6. При проверке качества зёрен пшеницы было установлено, что зёрна могут быть разбиты на 4 группы. К зёрнам первой группы принадлежит 96 %, второй – 2%, третьей и четвёртой – по 1% всех зёрен. Вероятности того, что зёрна дадут колос, содержащий не менее 50 зёрен, для семян указанных групп равны соответственно 0,5; 0,2; 0,18 и 0,2. Найти вероятность того, что из взятого наудачу зерна вырастет колос, содержащий не менее 50 зёрен.

Решение:

Решение:

Событие А = {выдержано качество зерен пшеницы},

Гипотеза H1 = { зёрна дадут колос, содержащий не менее 50 зёрен в первой группе},

Смотрите также файлы