Файл: Расчет на прочность и жесткость при простейших видах деформации.docx
Добавлен: 04.12.2023
Просмотров: 81
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3)
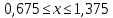
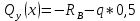
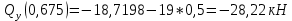
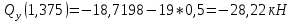
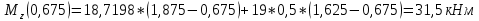
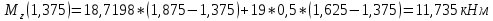
4)
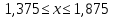
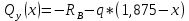
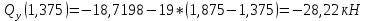
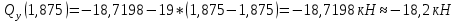
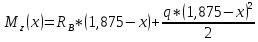
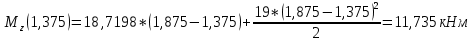
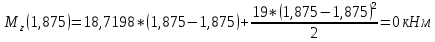
На основе полученных данных построим эпюры поперечных сил и изгибающих моментов:
Балка 3:
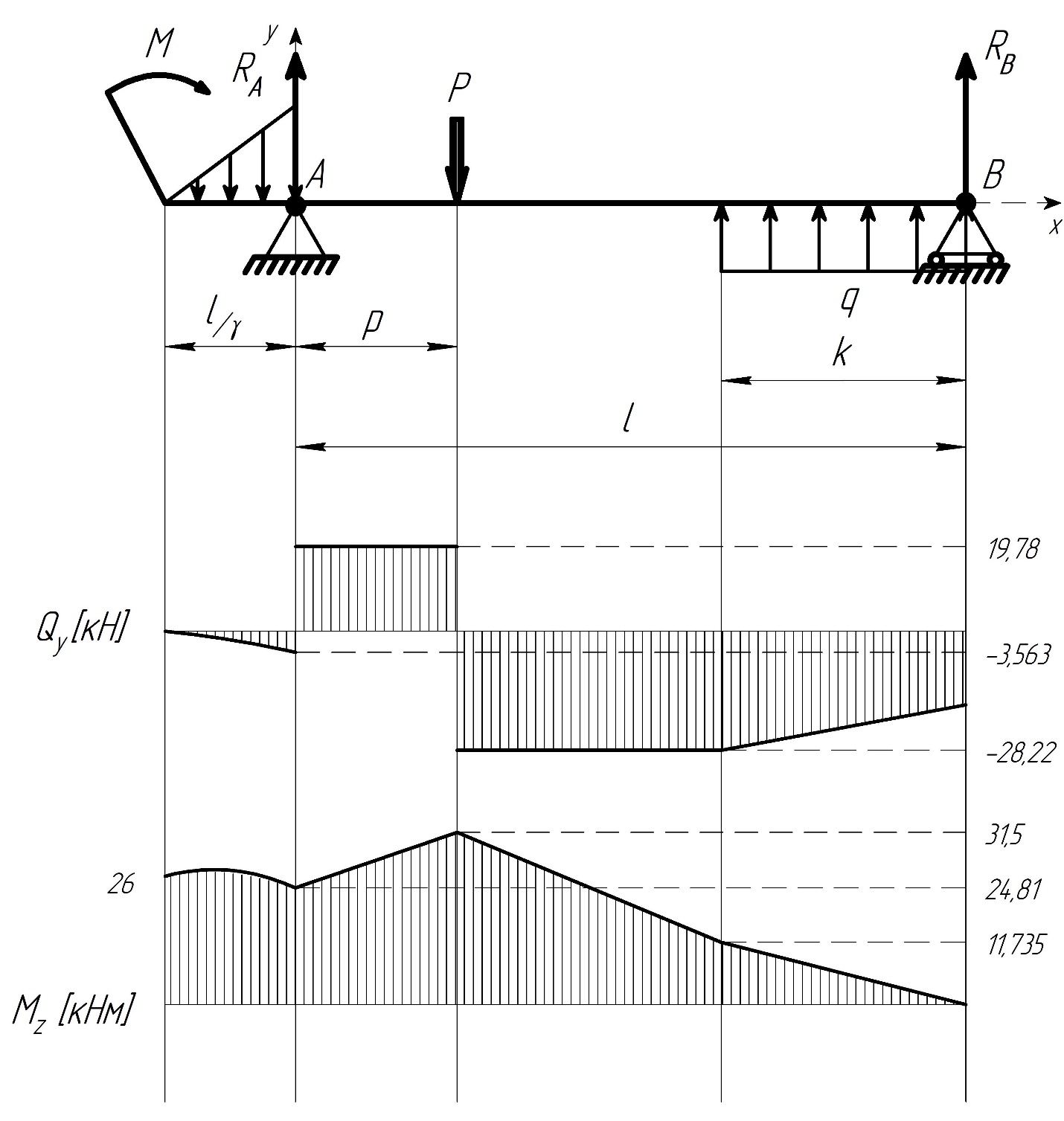
1.4. Для вычисления реакции опор составим уравнения равновесия:
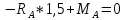
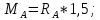
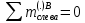
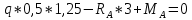
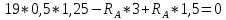
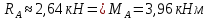
Определим Q и M на каждом участке:
1)
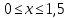
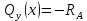
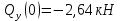
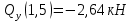
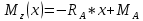
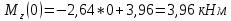
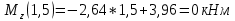
2)
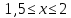
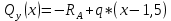
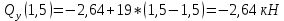
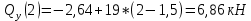
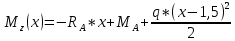
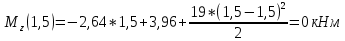
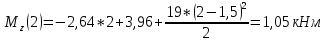
Найдем вершину параболы
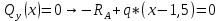
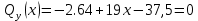
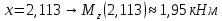
3)
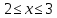
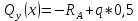
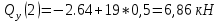
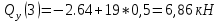
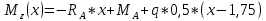
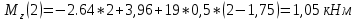
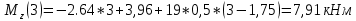
4)
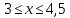
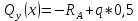
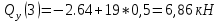
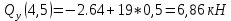
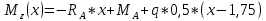
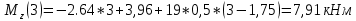
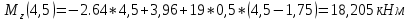
На основе полученных данных построим эпюры поперечных сил и изгибающих моментов:
Балка 4:
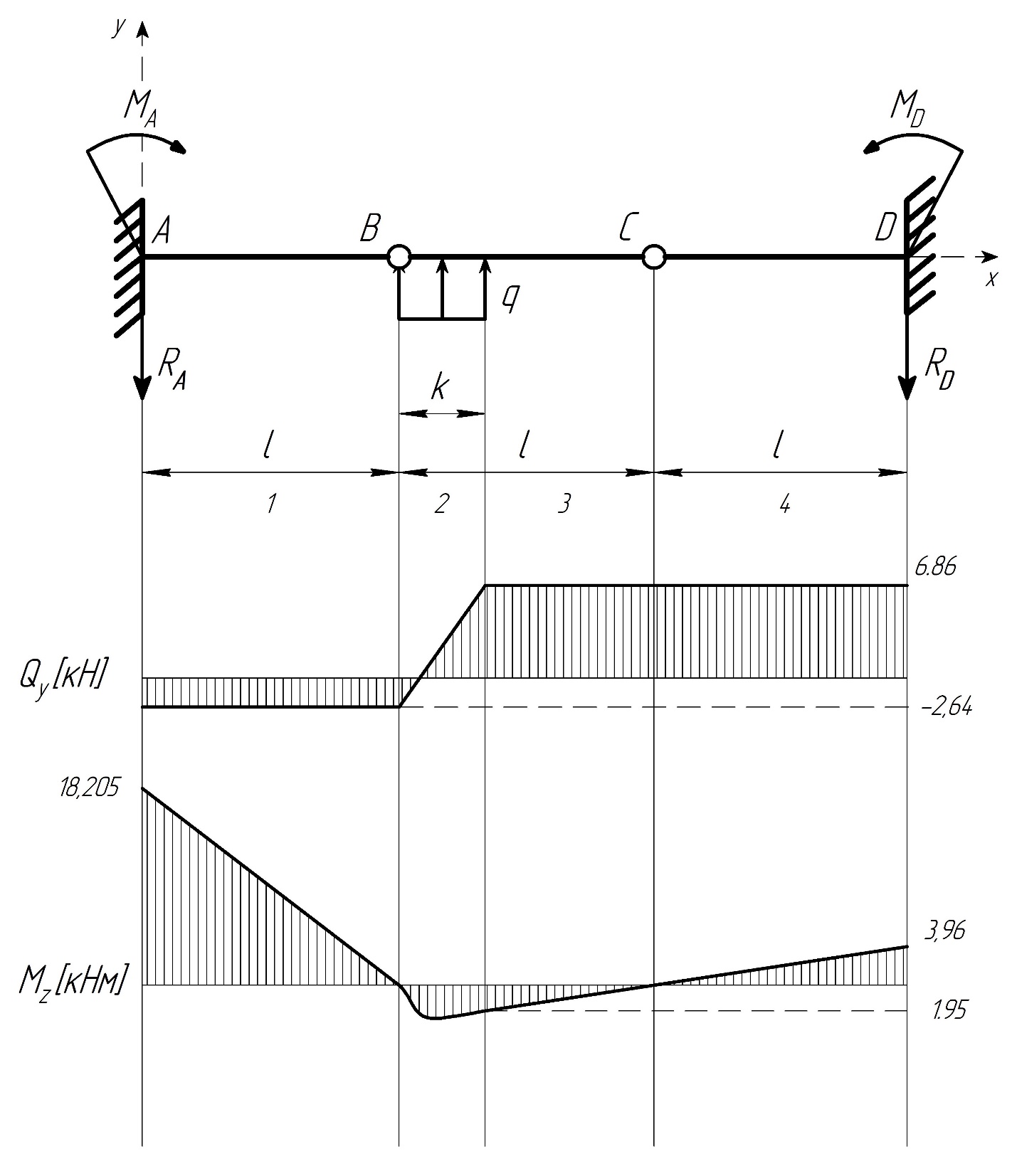
1.5 Для балки 5 по заданной эпюре изгибающих моментов, используя дифференциальные зависимости между силовыми факторами, строим эпюру поперечных сил и устанавливаем характер и величины нагрузок, приложенных к балке (M, P, q).
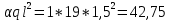
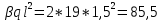
Рассмотрим каждый участок:
1)
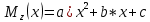
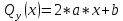
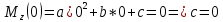
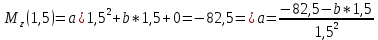
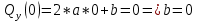
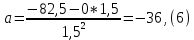
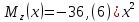
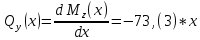
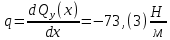
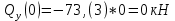
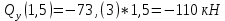
2)
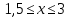
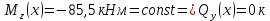
3)
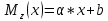
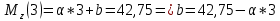
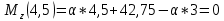
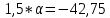
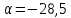
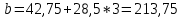
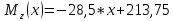
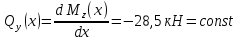
Определим величины нагрузок, приложенных к балке (M, P, q), исходя из эпюры:
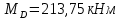
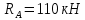
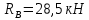
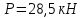
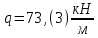
На основе полученных данных построим эпюры поперечных сил и установим характер и величины нагрузок, приложенных к балке:
Балка 5
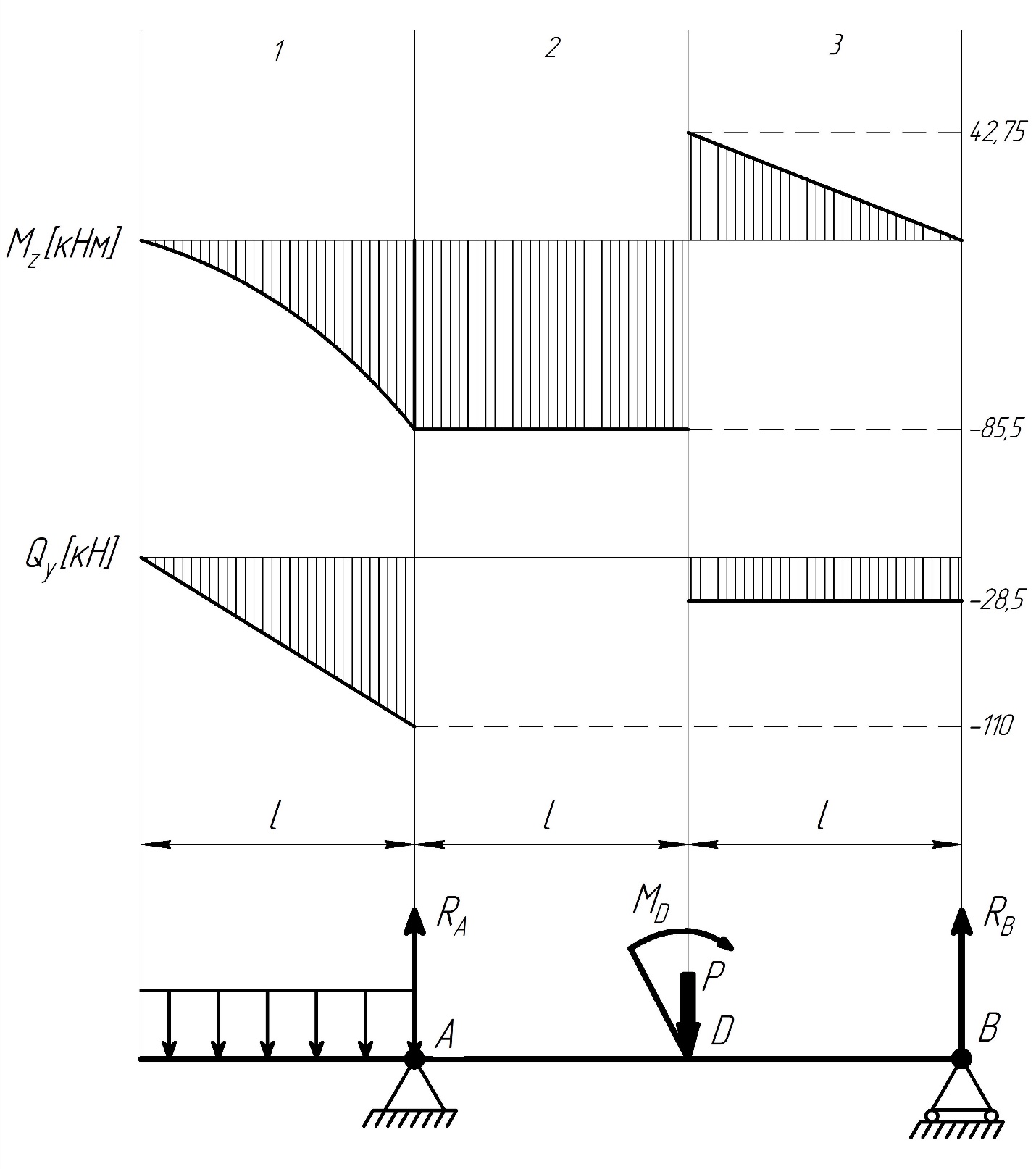
2.1 Для балка 2 подбираем двутавровое сечение, исходя из условия прочности по допускаемым напряжениям, если
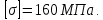
Строим эпюру распределения нормальных напряжений по высоте сечения, рассчитав
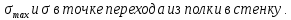
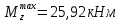
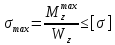
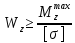
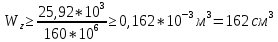
Из сортамента прокатной стали в соответствии с ГОСТ 8239.72 выбираем профиль №20 и
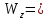184 
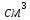
Дано (из сортамента):
h = 200 мм – высота балки
b = 100 мм – ширина полки
d = 5,2 мм – толщина стенки
t = 8,4 мм – средняя толщина полки
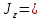1840 см4 – момент инерции
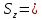104 см3 – статический момент полусечения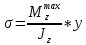
Из сортамента:
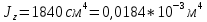
Считаем
в точках максимума:
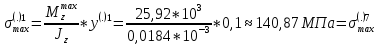
Считаем
в точке перехода балки в стенку: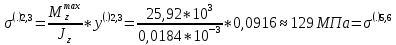
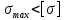– прочность обеспечена2.2 Подобранное сечение проверяем на прочность по касательным напряжениям, если
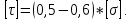Строим эпюру распределения касательных напряжений по высоте сечения, рассчитав 
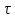во всех характерных точках.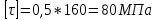
По формуле Журавского:
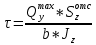
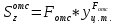
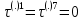, так как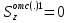 
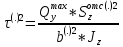
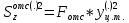
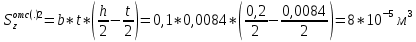
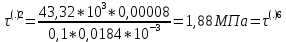
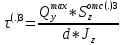
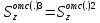
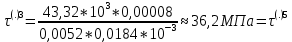
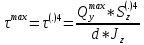
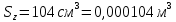– из сортамента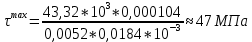
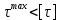– прочность по касательным напряжениям обеспеченаЭпюра распределения касательных напряжений по высоте сечения (двутавр):
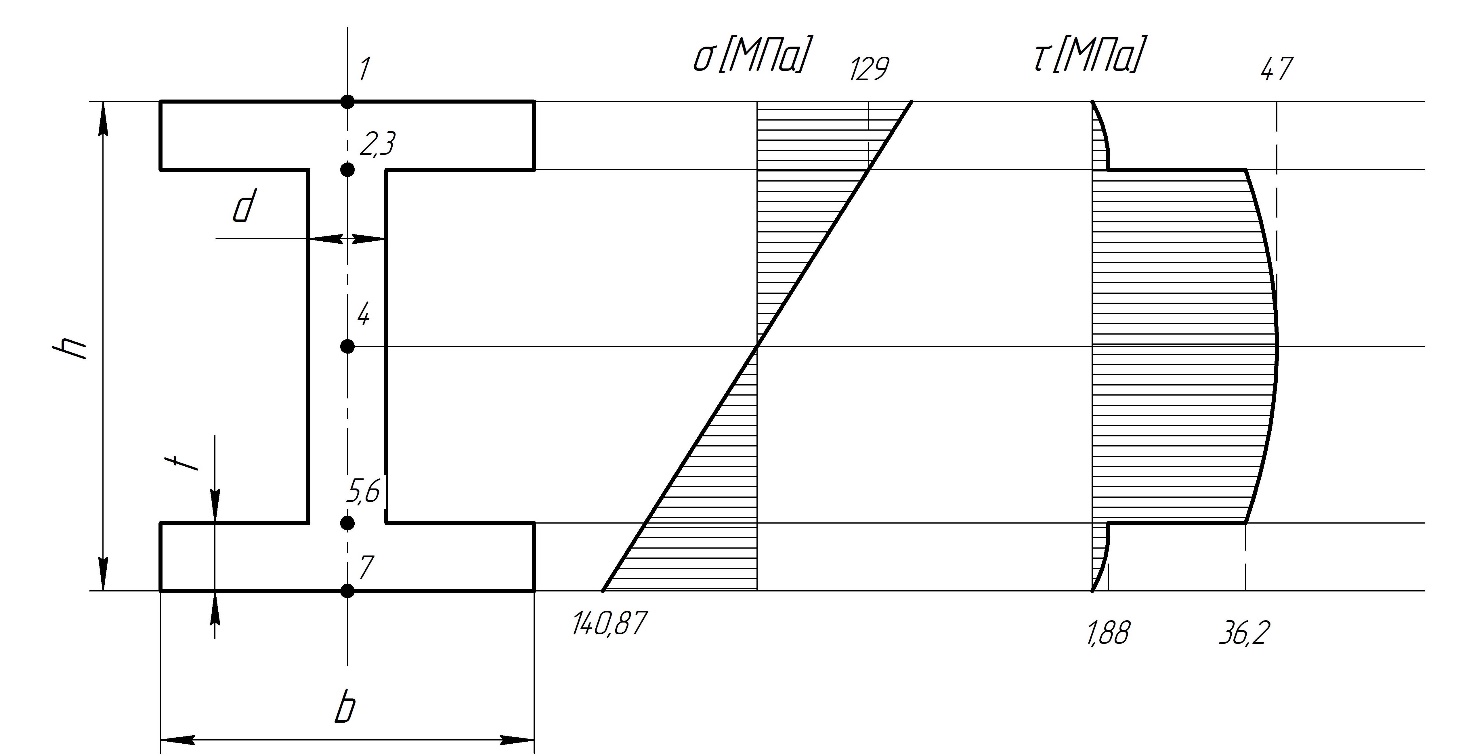
2.3 Пользуясь соотношением:
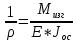и учитывая расположение опор, изображаем вид изогнутой оси балки: (
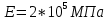– модуль упругости).Используя основное уравнение теории изгиба получим кривизну продольной оси балки в соответствующих участках:
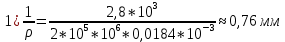
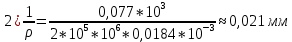
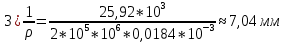
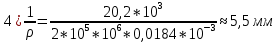
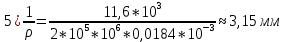
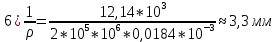
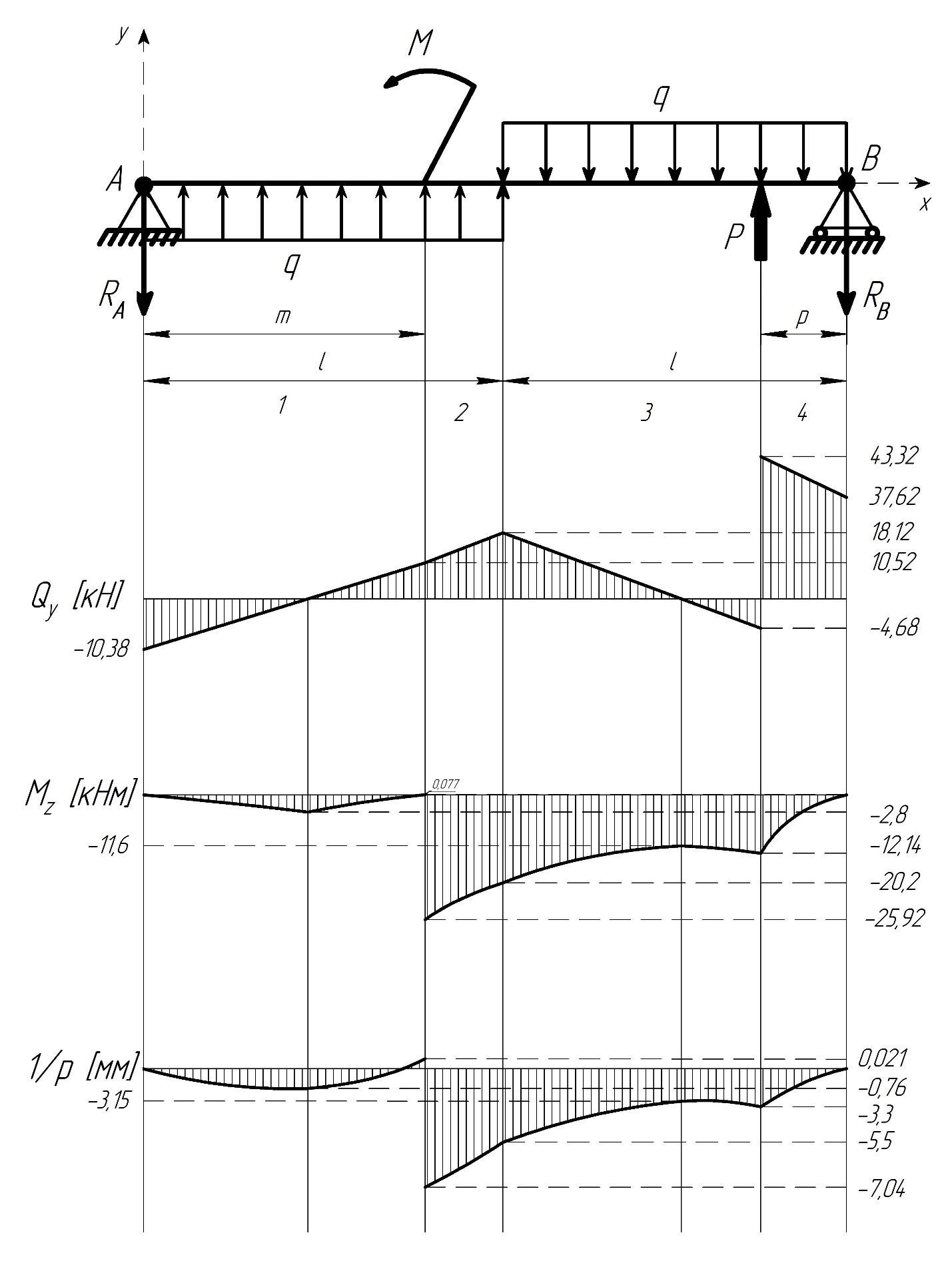
3. Для балка 1, изготовленной из хрупкого материала, имеющего различное сопротивление растяжению и сжатию, располагаем наиболее целесообразно сечение, форму и размеры которого мы взяли согласно варианту работы предварительно определив его геометрические характеристики и определяем допускаемое значение интенсивности распределенной нагрузки q, считая, что материал балки имеет:
