ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
Пусть
— конечное множество из 
элементов: 
.Симметрическая группа
степени — группа всех биекций (взаимно-однозначных отображений) 
множества в себя: 
. Число элементов (подстановок) симметрической группы: 
(число перестановок из ). Каждая биекция называется подстановкой (перестановкой) и записывается (природа элементов множества нас не интересует, значит можно считать, что элементы 
— числа):
Во второй строке записаны номера тех элементов, которым сопоставляются элементы из первой строки:
. Поэтому в написанной матрице столбцы можно как угодно переставлять, подстановка останется той же.Произведение двух подстановок
и 
— результат проведения сначала первой из них, а затем второй (композиция отображений): 
.
Для этого представляют столбцы
так, чтобы её первая строка совпадала со второй строкой 
; тогда 1-ая строка есть первая строка 
, а вторая строка — есть вторая строка .Некоторые математики иначе определяют произведение двух подстановок:
. (Это связано с тем, что произведение подстановок, по существу, означает композицию отображений, а математики не пришли к общему соглашению насчёт обозначения композиции отображений.) Соответственно, из-за этого меняется порядок умножения, в итоге результаты разнятся. Поэтому необходимо заранее обозначать композицию так, как будете её использовать.Пример. В данном примере показывается сама суть умножения подстановок.
Первая строка первой подстановки «взаимно-однозначно отображается на» вторую строку второй подстановки.
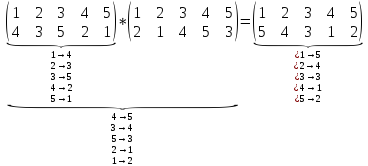
Пример.
Очевидно, что умножение перестановок ассоциативно, но не коммутативно.
Нейтральный элемент — это тождественная подстановка
.Обратный к
это 
, так как 
.
Таким образом, множество подстановок
-го порядка — множество, на котором введена замкнутая ассоциативная бинарная операция «умножение», на этом множестве есть нейтральный элемент, и все элементы этого множества обратимы, следовательно, множество подстановок образует мультипликативную группу. Эта группа называется симметрической группой степени и обозначается 
. Очевидно, что это конечная группа, и что порядок этой группы (число её элементов) равен 
.Примеры.
-
Запишем все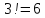
элементов (подстановок) симметрической группы 
:
;
-
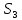Найт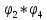и
и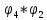 
:
Как видим
, то есть умножение подстановок некоммутативно.-
Найти обратную подстановку к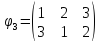
и проверить:
7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
Цикл длины
— симметрическая группа степени , в которой элементы перемещены так, что 
(или, что то же самое, 
), где все числа
— разные, 
. Цикл обозначается следующим образом:
или 
Причём набор таких элементов
называется 
орбитой любого из чисел .Цикл независим, если у него нет общих чисел. Цикл длины 1 — это, очевидно, тождественная подстановка
; в произведениях подстановок их можно не записывать.Теорема. Любую подстановку в
можно записать в виде произведения независимых циклов. Разложение подстановки в произведение циклов длины 
определено однозначно с точностью до порядка циклов.Доказательство.
Очевидно, что отношение между числами «принадлежность одной
-орбите» есть отношение эквивалентности:
-
Рефлексивно, то есть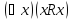
. -
Симметрично, то есть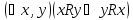
. -
Транзитивно, то есть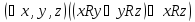
.
Данное отношение разбивает множество на классы эквивалентности по этому отношению. Каждый элемент принадлежит одному и только одному классу эквивалентности. Поэтому все числа
однозначно разбиваются на непересекающиеся классы эквивалентных между собой орбит, а подстановка представляется как произведение соответствующих циклов. Теорема доказана.Пример.
.Транспозиция — подстановка вида
, где 
, сводящаяся к перестановке двух чисел между собой, или, что тоже самое, цикл длины 2.Любой цикл можно написать в виде произведения транспозиций:
Замечание. Транспозиции не коммутируют (как и перестановки).
Пример.
.Пример.
.Пример.
.Пример.
.