Нетрудно показать, что любую подстановку можно представить в виде произведения транспозиций. Такое представление не единственно (например, в примерах выше ).

Все подстановки подразделяются на 2 класса: чётные и нечётные.

Если в матрице подстановки есть 2 столбца , для которых и или и , то такая пара столбцов называется инверсией подстановки.

Подстановка называется чётной или нечётной в зависимости от того, чётно или нечётно число инверсий в ней.

Очевидно, что любая транспозиция является нечётной подстановкой:

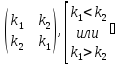одна инверсия нечётная

Теорема. Если подстановка чётная, то при любом способе разложения её в произведение транспозиций число множителей (то есть транспозиций) чётно, а если нечётная — то число этих транспозиций нечётно.

Следствие. Так как при перемножении чётных подстановок, очевидно, снова получается чётная подстановка, то множество всех чётных подстановок является подгруппой симметрической группы и называется знакопеременной группой и обозначается . Причём порядок равен . состоит из одной подстановки: . состоит из подстановок и т. д.

---

Пример. Подгруппа симметрической группы состоит из 3-х подстановок:



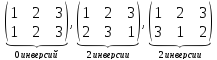
Произведение двух нечётных подстановок, очевидно, есть чётная подстановка, поэтому нечётные подстановки не образуют группу.

Порядок подстановки — это наименьшее целое положительное число такое, что .

Пример. Докажем, что порядок подстановки равен 5:





Теорема. Порядок подстановки равен НОК длин всех её независимых циклов.

Также нетрудно показать, что порядок цикла равен длине цикла.

Пример. Определить, является ли подстановка чётной или нечётной и разложить её в произведение транспозиций:



Сосчитаем число инверсий . Инверсии — это пары столбцов , , , , , , . Поэтому (подстановка нечётная).

Разложим её на циклы:

Как видим, число транспозиций в произведении равно 5, то есть нечётно.

Обратная операция:

добавлена в середину только потому, что она равна . Другие подстановки (не равные ) в любое место добавлять нельзя, так как коммутативности нет.

Порядок подстановки: . То есть . Проверим это.

---

Смотрите также файлы

• 1. Биологическая роль бора.docx

• Практическая работа по учебной дисциплине Экономика Выполнил студент Факультет зо курс 2 шифр 203121 гр. Ист 2к.docx

• Повторение и обобщение по разделу Политика.docx

• 1 арышайла сзіні аудармасы 2 Байоыр арышайлаы ай облыста орналасан.docx

• Урока Обмен данными между программами Цели обучения, которым способствует.docx