ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, х ≠ 3
у > 3, если х > 0, х ≠ 3.

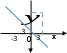
▲
9) Построить график функции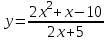 . Найти область значений.
. Найти область значений.
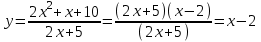 , х ≠ -2,5
, х ≠ -2,5
E(y) = (-∞; ∞), у ≠ -4,5.

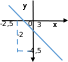
▲
10) Постройте график функции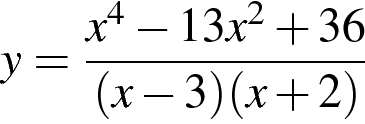 и определите, при каких значениях параметра
и определите, при каких значениях параметра 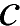 прямая
прямая 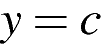 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
▼Разложим числитель дроби на множители:
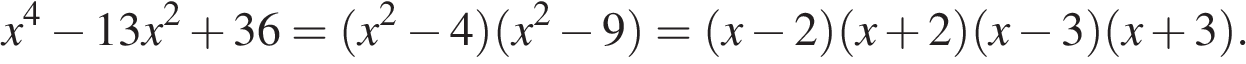
При и
и 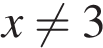 функция принимает вид:
функция принимает вид:
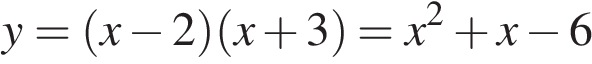 ,
,
её график — парабола c выколотыми точками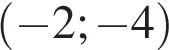 и
и 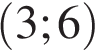 .
.
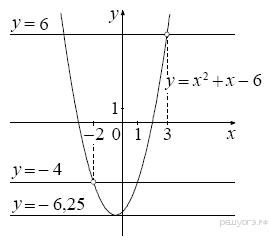
Прямая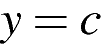 имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты
имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты
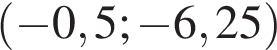 .
.
Поэтому ,
, 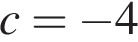 или
или  .▲
.▲
11) При каком значении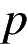 прямая
прямая 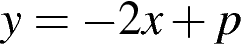 имеет с параболой
имеет с параболой 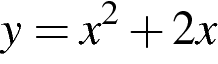 ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении 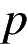 .
.
▼ График функции изображён на рисунке.
2. Задание 23 № 127
При каком значении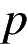 прямая
прямая 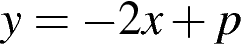 имеет с параболой
имеет с параболой 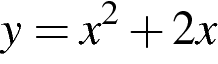 ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении 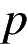 .
.
▼ График функции изображён на рисунке.
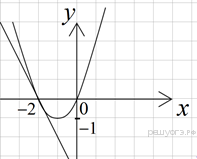
Запишем условие общей точки: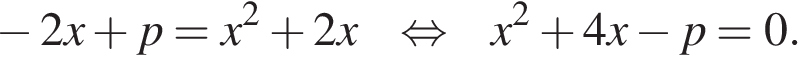
Прямая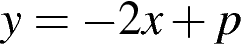 будет иметь с параболой единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю: D =
будет иметь с параболой единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю: D = 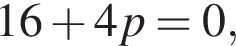
откуда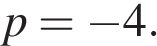 Подставив значение параметра в уравнение, находим
Подставив значение параметра в уравнение, находим 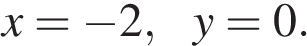
Ответ: p = −4, координата точки: (−2;0).▲
12) Известно, что парабола проходит через точку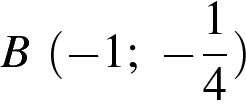 и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую 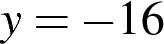 .
.
▼Уравнения параболы, вершина которой находится в начале координат: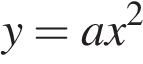 . Парабола проходит через точку
. Парабола проходит через точку 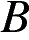 , поэтому
, поэтому 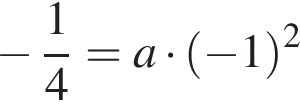 , откуда
, откуда 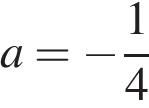 . Уравнение параболы:
. Уравнение параболы: 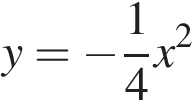 . Абсциссы точек пересечения с прямой
. Абсциссы точек пересечения с прямой 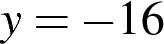 найдем из уравнения
найдем из уравнения 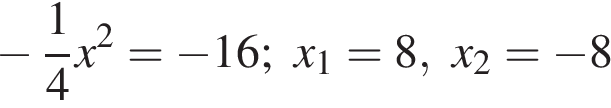 .
.
Ответ: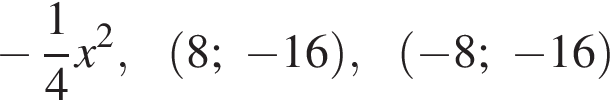 .▲
.▲
13) Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.
▼Одна из возможных форм записи уравнения параболы в общем виде выглядит так: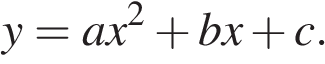 Координата
Координата 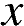 вершины параболы находится по формуле
вершины параболы находится по формуле 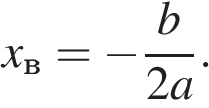
Координату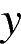 вершины параболы найдётся подстановкой
вершины параболы найдётся подстановкой 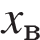 в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов 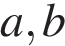 и
и 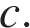 Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
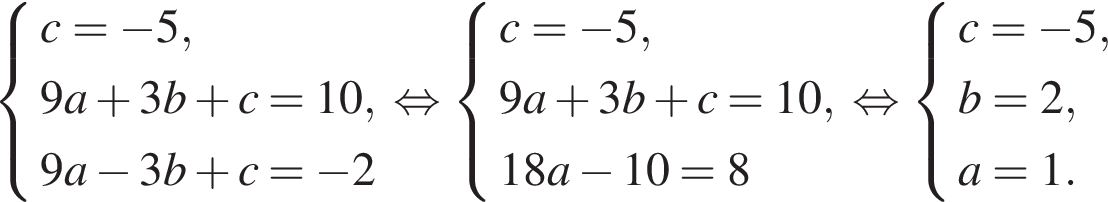
Найдём координаты вершины:
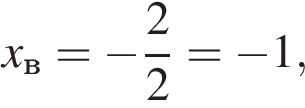
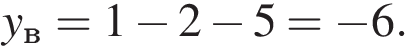
Ответ: (−1; −6).▲
14) При каких значениях вершины парабол
вершины парабол 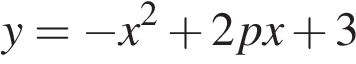 и
и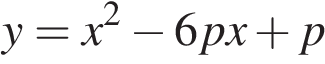 расположены по разные стороны от оси
расположены по разные стороны от оси  ?
?
▼Координата вершины параболы определяется по формуле
вершины параболы определяется по формуле  Координата
Координата 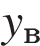 вершины находится подстановкой
вершины находится подстановкой 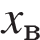 в уравнение параболы. Вершины парабол будут находится по разные стороны от оси
в уравнение параболы. Вершины парабол будут находится по разные стороны от оси  , если координаты их вершин имеют разные знаки. Вспомнив, что два сомножителя имеют разный знак тогда и только тогда, когда их произведение отрицательно, составим и решим неравенство:
, если координаты их вершин имеют разные знаки. Вспомнив, что два сомножителя имеют разный знак тогда и только тогда, когда их произведение отрицательно, составим и решим неравенство:
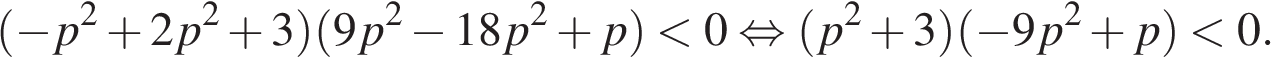
Заметим, что первый множитель всегда больше нуля, поэтому на него можно разделить.
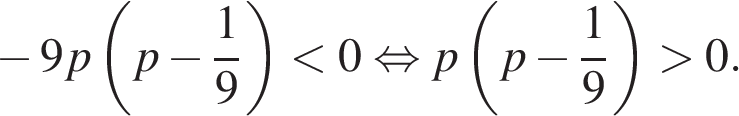
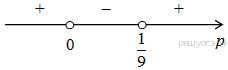
Произведение двух сомножителей будет больше нуля, если сомножители имеют одинаковый знак (см. рисунок). Таким образом, получаем ответ:
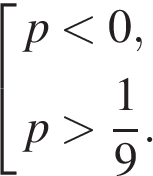
Ответ: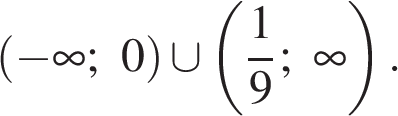 ▲
▲
15) При каких значениях p вершины парабол
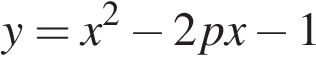 и
и 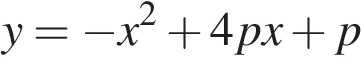
расположены по разные стороны от оси x?
▼ Абсцисса вершины параболы определяется по формуле Для данных парабол это точки p и 2p.
Для данных парабол это точки p и 2p.
Ордината вершины находится подстановкой
вершины находится подстановкой  в уравнение параболы. Для данных парабол получаем:
в уравнение параболы. Для данных парабол получаем:
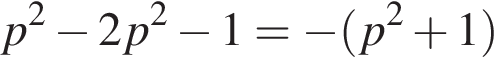 и
и 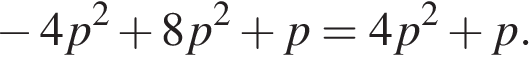
Вершины парабол находятся по разные стороны от оси абсцисс, если ординаты их вершин имеют разные знаки.
Два множителя имеют разные знаки тогда и только тогда, когда их произведение отрицательно. Тем самым, требуется решить неравенство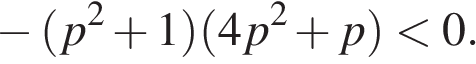 Заметим, что первый множитель меньше нуля при всех значениях p, поэтому на него можно разделить, изменив знак неравенства на противоположный. Имеем:
Заметим, что первый множитель меньше нуля при всех значениях p, поэтому на него можно разделить, изменив знак неравенства на противоположный. Имеем:
у > 3, если х > 0, х ≠ 3.


▲
9) Построить график функции
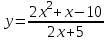 . Найти область значений.
. Найти область значений.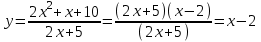 , х ≠ -2,5
, х ≠ -2,5E(y) = (-∞; ∞), у ≠ -4,5.


▲
10) Постройте график функции
▼Разложим числитель дроби на множители:
При
её график — парабола c выколотыми точками

Прямая
Поэтому
11) При каком значении
▼ График функции изображён на рисунке.
2. Задание 23 № 127
При каком значении
▼ График функции изображён на рисунке.

Запишем условие общей точки:
Прямая
откуда
Ответ: p = −4, координата точки: (−2;0).▲
12) Известно, что парабола проходит через точку
▼Уравнения параболы, вершина которой находится в начале координат:
Ответ:
13) Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.
▼Одна из возможных форм записи уравнения параболы в общем виде выглядит так:
Координату
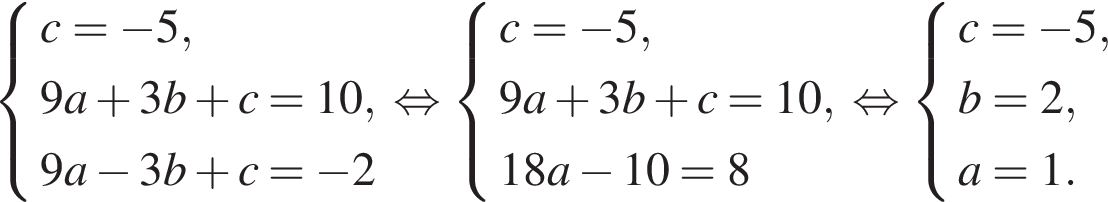
Найдём координаты вершины:
Ответ: (−1; −6).▲
14) При каких значениях
▼Координата
Заметим, что первый множитель всегда больше нуля, поэтому на него можно разделить.
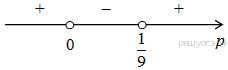
Произведение двух сомножителей будет больше нуля, если сомножители имеют одинаковый знак (см. рисунок). Таким образом, получаем ответ:
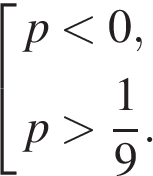
Ответ:
15) При каких значениях p вершины парабол
расположены по разные стороны от оси x?
▼ Абсцисса вершины параболы определяется по формуле
Ордината
Вершины парабол находятся по разные стороны от оси абсцисс, если ординаты их вершин имеют разные знаки.
Два множителя имеют разные знаки тогда и только тогда, когда их произведение отрицательно. Тем самым, требуется решить неравенство