Каждая эпоха начинается с того, что у оптимайзера обнуляются градиенты. После этого считаем forward, то есть мы берём наш весь X_train и передаём его в функцию forward, считаем prediction (считаем предсказания нашей нейросети), после этого считаем функцию потерь, получаем некоторое число – скаляр, по которому мы можем сделать backward. Делаем по этому скаляру backward, то есть это некоторый тензор, который зависит от параметров сети, то есть от весов нейросети, который обернут в оптимайзер, и, соответственно, когда мы делаем loss_val.backward, оптимайзер понимает, что там посчитались градиенты, и значит оптимайзер может сделать шаг. Это весь цикл обучения на одной эпохе.  Давайте проведём обучение на 2000 эпохах и посмотрим, что получится.

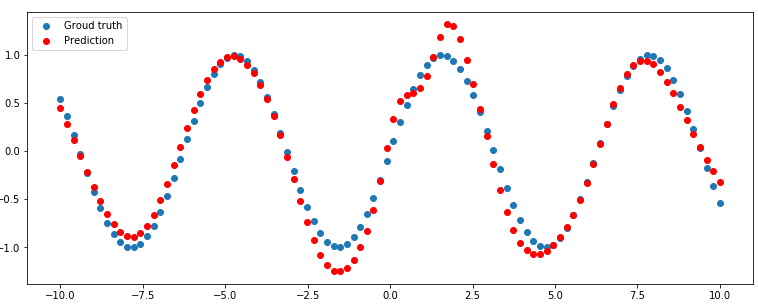
Мы видим, что результат хороший. Мы обучались на зашумлённых данных, которые совсем не похожи на синусы.  Получили некоторые точки, которые здесь отмечены красным. Оказывается, что у нас довольно хорошие результаты, мы обучались на зашумлённых данных, а получили действительно функцию, которая очень близка к синусу. Она не идеальный синус потому что данные, которые приходили, объективно были не очень похожи на идеальный синус.

12. Посмотрим, как можно улучшить результаты. Во-первых, мы могли взять и поставить поменьше нейронов в нашем единственном скрытом слое. Поставим, например, один нейрон. Что будет в таком случае? Передаём параметры нейросети в оптимайзер. Можно ещё раз инициировать loss function, это ни на что не влияет. И обучимся заново. Можно увидеть, что если всего один нейрон, то у нас получается практически линейное предсказание. Наверное, одного нейрона недостаточно, наша нейросеть не очень сложная, она не может предсказать сложную функцию.

Давайте добавим ещё нейронов (например, 3), у нас получится уже один изгиб. Можно заметить интересную закономерность: чем больше нейронов мы используем в скрытом слое, тем больше изгибов у нашей итоговой функции получается. Если вы представите эту нейросеть, то это простая сумма сигмоид. В нашем скрытым слое есть N сигмоид.

Это частый случай, когда создана нейронная сеть более сложная, чем требуется, которая может аппроксимировать более сложные функции, чем та функция, которую мы имеем. Переусложнение нейронной сети – это не всегда плохо.

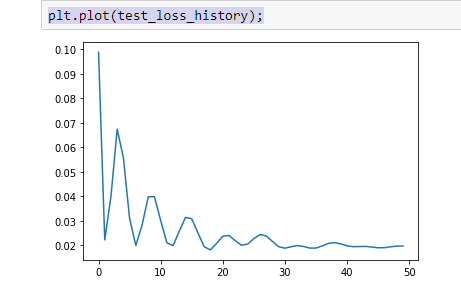
14. Для визуализации процесса обучения по эпохам можно добавить код, показанный красным жирным шрифтом. Вид функции ошибки по эпохам (для 50 эпох) показан на графике.

---

##
import torch

import matplotlib.pyplot as plt

##
##

import matplotlib

matplotlib.rcParams['figure.figsize'] = (13.0, 5.0)

##

##

x_train = torch.rand(100)

x_train = x_train * 20.0 - 10.0

y_train = torch.sin(x_train)

plt.plot(x_train.numpy(), y_train.numpy(), 'o')

plt.title('$y = sin(x)$');

##

##

noise = torch.randn(y_train.shape) / 5.

plt.plot(x_train.numpy(), noise.numpy(), 'o')

plt.axis([-10, 10, -1, 1])

plt.title('Gaussian noise');

y_train = y_train + noise

plt.plot(x_train.numpy(), y_train.numpy(), 'o')

plt.title('noisy sin(x)')

plt.xlabel('x_train')

plt.ylabel('y_train');

##

##

x_train.unsqueeze_(1)

y_train.unsqueeze_(1);

##

##

x_validation = torch.linspace(-10, 10, 100)

y_validation = torch.sin(x_validation.data)

plt.plot(x_validation.numpy(), y_validation.numpy(), 'o')

plt.title('sin(x)')

plt.xlabel('x_validation')

plt.ylabel('y_validation');
x_validation.unsqueeze_(1)

y_validation.unsqueeze_(1);

##

##

class SineNet(torch.nn.Module):

def __init__(self, n_hidden_neurons):

super(SineNet, self).__init__()

self.fc1 = torch.nn.Linear(1, n_hidden_neurons)

self.act1 = torch.nn.Sigmoid()

self.fc2 = torch.nn.Linear(n_hidden_neurons, 1)
def forward(self, x):

x = self.fc1(x)

x = self.act1(x)

x = self.fc2(x)

return x
sine_net = SineNet(50)

##

##

def predict(net, x, y):

y_pred = net.forward(x)
plt.plot(x.numpy(), y.numpy(), 'o', label='Groud truth')

plt.plot(x.numpy(), y_pred.data.numpy(), 'o', c='r', label='Prediction');

plt.legend(loc='upper left')

plt.xlabel('$x$')

plt.ylabel('$y$')
predict(sine_net, x_validation, y_validation)

##

##

optimizer = torch.optim.Adam(sine_net.parameters(), lr=0.01)

##
#test_accuracy_history = []

#test_loss_history = []
##

def loss(pred, target):

squares = (pred - target) ** 2

return squares.mean()

##

##

for epoch_index in range(2000):

optimizer.zero_grad()
y_pred = sine_net.forward(x_train)

loss_val = loss(y_pred, y_train)
loss_val.backward()
optimizer.step()
# test_preds = sine_net.forward(x_validation)

# test_loss_history.append(loss(test_preds, y_validation))
predict(sine_net, x_validation, y_validation)

##

##

#plt.plot(test_loss_history);

##


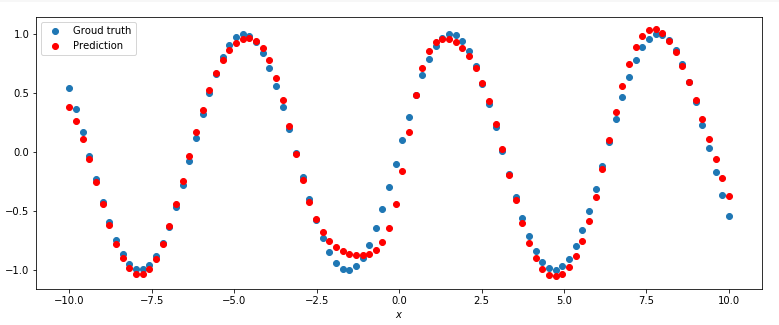
Задание на лабораторную работу

1. 
   Исследовать нейронную сеть при заданных начальных параметрах (см. таблицу). Найти минимальное значение n_hidden_neurons, при котором сеть дает удовлетворительные результаты.
   
2. 
   Найти наилучшее значение шага градиентного спуска lr в интервале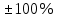 от номинального значения.
   
3. 
   Изменить нейронную сеть для предсказания функции y = 2^x * sin(2^−x)
   
4. 
   Для этой задачи (п. 3) получите метрику MAE =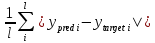
   

---

не хуже 0.03, варьируя: архитектуру сети, loss-функцию, lr оптимизатора или количество эпох в обучении.

5. 
   Метрика вычисляется с помощью выражения (pred - target).abs().mean() и выводится оператором
   

print(metric(sine_net.forward(x_validation), y_validation).item()).


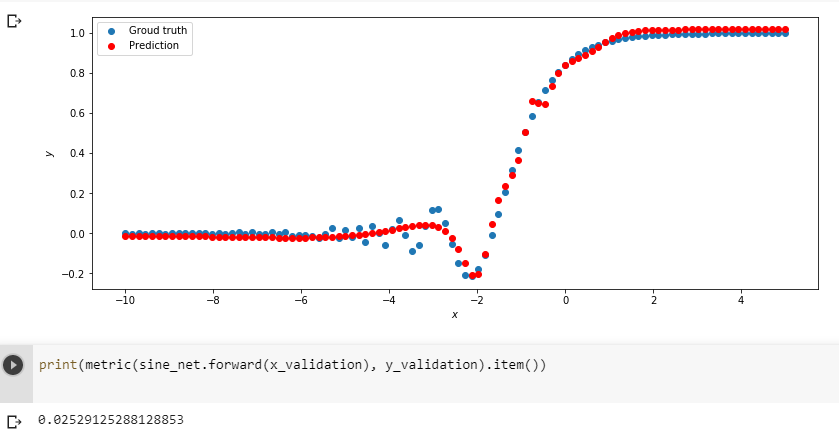
Таблица. Начальные значения гиперпараметров нейронной сети

Вариант	Метод оптимизации	Число нейронов в скрытом слое n_hidden_neurons	Шаг градиентного спуска lr
0	ADAM	10	0.01
1	ADAM	20	0.001
2	ADAM	30	0.01
3	ADAM	40	0.001
4	ADAM	50	0.01
5	SGD	10	0.001
6	SGD	20	0.01
7	SGD	30	0.001
8	SGD	40	0.01
9	SGD	50	0.001

Примечание

1. 
   Подготовка данных для функции y = 2^x * sin(2^−x)
   

def target_function(x):

return 2**x * torch.sin(2**-x)
# ------Dataset preparation start--------

x_train = torch.linspace(-10, 5, 100)

y_train = target_function(x_train)

noise = torch.randn(y_train.shape) / 20.

y_train = y_train + noise

x_train.unsqueeze_(1)

y_train.unsqueeze_(1)
x_validation = torch.linspace(-10, 5, 100)

y_validation = target_function(x_validation)

x_validation.unsqueeze_(1)

y_validation.unsqueeze_(1)

# ------Dataset preparation end--------

2. 
   Описаниефункцииmetric
   

---

def metric(pred, target):

     return (pred - target).abs().mean()

Содержание отчета

1. 
   Титульный лист
   
2. 
   Цель работы, постановка задачи исследования.
   
3. 
   Описание методики исследования.
   
4. 
   Результаты исследования в соответствии с заданием.
   
5. 
   Выводы по работе.
   

---

Смотрите также файлы

• Суммативное оценивание за раздел Строение атома, атомные явления. Атомное ядро Цели обучения.docx

• Торт Клубничный.docx

• Согласно Письму Минобразования рф (от 12. 08. 2002, 13519914) О введении третьего дополнительного часа фк в образовательные учреждения рф, в практику школ рекомендуется ввести в недельную нагрузку 3ий урок.docx

• Традиции и фольклор.doc

• Что же такое позитивизм Позитивизм.docx