Вопрос 1ВерноБаллов: 1,000 из 1,000Предел lim\limitx→∞(x−3x+2)^2x−1=e^t , где значение t равноОтвет:-10ВерноВопрос 2ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаФункция y=log2(x−1)монотонно возрастающей Вернонеограниченной ВерноВопрос 3НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаЗначение аогумента, при котором происходит разрыв функции, −это ###.Ответ: точки разрыва НеверноВопрос 4ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПредел функции lim\limit_x→3 arcsin(x−3)/sin(6−2x)равен:Выберите один ответ:2−0,5 Верно0,5−20Вопрос 5ВерноБаллов: 1,000 из 1,000Множество занчений аргумента, при которых функция имеет математический смысл - это ### функции.Ответ: Область определения ВерноВопрос 6ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПредел lim\limit_x→2tg(x−2)/ln(3−x)равен:Выберите один ответ:−1 ВерноВопрос 7ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаСоответствие между функциями и свойствами функций:y−x1+x2 нечетная Верноy=x21+x4 четная Верноy=23x−1 монотонно возрастающая на всей области определения ВерноВопрос 8ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаОбластью определения функции y=√4−x2является множество:[−2;2] ВерноВопрос 9ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаНа числовой прямой дана точка x=4,5. Тогда её ε-окрестностью является интервал:(4,3;4,7) ВерноВопрос 10Частично правильныйБаллов: 0,500 из 1,000Не отмеченоОтметить вопросТекст вопросаСоответствие между функциями и видом разрыва в точке x=2y=x2−4x2−x−2 Ответ 1 неустранимый разрыв первого рода Неверноy=1x−2 разрыв второго рода ВерноВопрос 1ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПроизводная функции y=5x2−x−−√+3 имеет вид

---

:

Выберите один ответ:

x2−12x√+3

10x−12x√ Верно

10x−12x√+3

5x−1x√

Вопрос 2

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

На рисунке изображён график производной функции y=f(x)

, заданной на отрезке [−1;8] Тогда точкой минимума этой функции является:

Выберите один ответ:

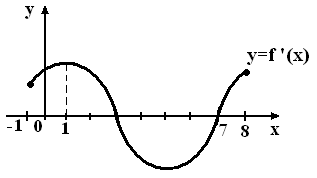
1

8

7 Верно

−1

Вопрос 3

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

На рисунке изображён график функции y=f(x) на отрезке [a;b].

Тогда эта функция удовлетворяет условиям:

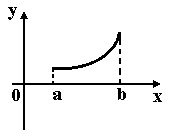
Выберите один ответ:

y′>0;y′′<0

y′>0;y′′>0 Верно

y′<0;y′′<0

y′<0;y′′>0

Вопрос 4

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

Производная функции y=√cosx+4 в точке x=π2 равна:

Выберите один ответ:

−14 Верно
Вопрос 5

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

Предел lim\limitx→∞ln(2x+1)x+3 равен:

Выберите один ответ:

0 Верно

1

3

2

Вопрос 6

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Производная функции y=2sinx равна:

Выберите один ответ:

2cosx⋅ln2\cdosinx

2sinx⋅cosx

2cosx

2sinx⋅ln2⋅cosx Верно

2cosx⋅ln2

Вопрос 7

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

Предел lim\limitx→∞x3e2x равен:

Ответ: 0 Верно

Вопрос 8

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

Дифференциал функции y=√2x−3

имеет вид:

Выберите один ответ:

dy=22x−3−−−−−√dx

dy=122x−3√dx

dy=12x−3dx

dy=12x−3√dx Верно


Вопрос 9

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

Производная функции y=x2⋅tg(3x) равна:

Выберите один ответ:

2x⋅tg(3x)+x2⋅3cos2x

2x\cdotg(3x)+x2⋅3cos2(3x) Верно

2x⋅1cos2(3x)

2x⋅1cos2x

2x⋅3cos2(3x)

Вопрос 10

Верно

Баллов: 1,000 из 1,000

Не отмеченоОтметить вопрос

Текст вопроса

Пределы функций, которые можно вычислить с помощью правила Лопиталя:

Выберите один или несколько ответов:

lim\limitx→23x−15x+2

lim\limitx→∞sinxx

lim\limitx→∞e2x−e3xx Верно

lim\limitx→0sin6xe3x−1

---

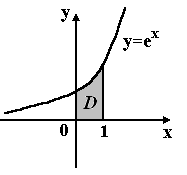
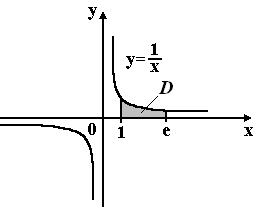
ВерноВопрос 1ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПлощадь криволинейной трапеции D равна:Выберите один ответ:e+1e−1 ВерноВопрос 2ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПлощадь фигуры, изображенной на рисунке, равнаОтвет:1ВерноВопрос 3ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаМножество первообразных для функции f(x)=sin5xимеет вид:Выберите один ответ:15cos5x+C5cos5x+C−15cos5x+C Верноcos5x+CВопрос 4НеверноБаллов: 0,000 из 1,000Определенный интеграл ∫0412x+1√dxравенОтвет: 0НеверноВопрос 5НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаЗначение определенного интеграла ∫10(x3+2x)dxравноОтвет: -1НеверноВопрос 6ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаОпределенный интеграл численно равен ### криволинейной трапеции.Ответ: Площади ВерноВопрос 7ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаНеопределенный интеграл ∫e8xdxравен:Выберите один ответ:18ex+C8e8x+C18e8x+C ВерноВопрос 8ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаФормула ∫udv=uv−∫vdu называется формулой интегрирования ###.Ответ: по частям ВерноВопрос 9ВерноБаллов: 1,000 из 1,000Текст вопроса Известны значения определенных интегралов ∫10f(x)dx=3и ∫40f(x)dx=2. Тогда значение интеграла ∫41f(x)dxравно Ответ: -1 ВерноВопрос 10НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаМножество первообразных для функции (3x−8)9имеет вид:Выберите один ответ:130(3x−8)9+C13(3x−8)9+C Неверно130(3x−8)10+C(3x−8)10+CВопрос 1ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаЗамена Бернулли для решения линейного дифференциального уравнения первого порядка имеет вид

---

Выберите один ответ:y=ux,y′=u′x+uy=uv,y′=u′v+uv′ Верноy′=kyy=uv,y′=u′v−uv′v2Вопрос 2ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаСоответствие между дифференциальными уравнениями и их видами:y′−x4y=0 Ответ 1линейное однородное дифференциальное уравнение Верно3y′′−5y′+10y=sinx Ответ 2 линейное дифференциальное уравнение с постоянными коэффициентами и правой частью специального вида Верно(x+2)y′′+y′+10y=x4 Ответ 3 линейное неоднородное дифференциальное уравнениеВерноy′′+4y′−5y=0 Ответ 4 линейное однородное дифференциальное уравнение с постоянными коэффициентами ВерноВопрос 3ВерноБаллов: 1,000 из 1,000Общим интегралом дифференциального уравнения F(x,y,y′,…,y(n))=0является семейство функций видаВыберите один ответ:Ф(x,y,C1,C2)=0Ф(x,y,C1,…,Cn)=0 Верноy=C1φ(x)+C2y=φ(x,C)Вопрос 4НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПорядок дифференциального уравнения 6y′′′−2y′′+5y′=4x2+2равенВыберите один ответ:2−26 Неверно3Вопрос 5ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаОбщий интеграл дифференциального уравнения dyy=sinxdxимеет видВыберите один ответ:ln|y|=cosx+Cy=ecosx+C1y2=cosx+Cln|y|=−cosx+C ВерноВопрос 6ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаСреди приведенных систем задачей Коши являетсяВыберите один ответ:{y′′+2y′−2y=0,y(0)=1{y′′+2y′−2y=0,y(0)=1,y(1)=1{y′′+2y′−2y=0,y(0)=y′(0)=1 Верно{y′′+2y′−2y=0,y′(0)=1Вопрос 7ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаДифференциальное уравнение y′′+x2y′−2y=cosx являетсяВыберите один ответ:линейным неоднородным уравнением ВерноВопрос 8ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаОбщее решение линейного однородного дифференциального уравнения y′′−2y′+2y=0 имеет видВыберите один ответ:

---

C1cosx+C2sinxe−x(C1cosx+C2sinx)ex(C1cosx+C2sinx) ВерноC1ex+C2e−xВопрос 9ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаСумма параметров α и β, при которых уравнение y′′+(y′′)α−β+5⋅y′+exy=x(8−2β)является линейным однородным дифференциальным уравнением, равнаОтвет: 3 ВерноВопрос 10ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаФундаментальная система решений линейного однородного дифференциального уравнения y′′−4y′+4y=0имеет видВыберите один ответ:y1=e2x,y2=xe2x Верноy1=e−2x,y2=e−2xВопрос 1ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаПятый член ряда ∑n=1∞n2(n+19)n!равенОтвет: 5 ВерноВопрос 2ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаРадиус сходимости степенного ряда ∑n=0∞xnn+1 равенВыберите один ответ:1 Верно∞π(π≈3,14)0Вопрос 3НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаСходящимися рядами являютсяВыберите один ответ:∑n=1∞3−n∑n=1∞1n−−√∑n=1∞2n∑n=1∞1n НеверноВопрос 4ВерноБаллов: 1,000 из 1,000Не отмеченоОтметить вопросТекст вопросаНеобходимым условием сходимости ряда ∑n=1∞un являетсяВыберите один ответ:limn→∞un=0 Верноlimn→∞un≠0limn→∞un>0limn→∞∑n=1mun=0Вопрос 5НеверноБаллов: 0,000 из 1,000Для числового ряда ∑n=1∞2nn! с общим членом un предел limn→∞un+1un равенОтвет: 3НеверноВопрос 6НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаЦентр области сходимости степенного ряда ∑n=0∞(x+3)n2n+1находится в точке x,равнойОтвет: 0 НеверноВопрос 7НеверноБаллов: 0,000 из 1,000Не отмеченоОтметить вопросТекст вопросаСходящимися рядами являютсяВыберите один или несколько ответов:∑n=1∞1n−−√3∑n=1∞1n2 Верно∑n=1∞12n∑n=1∞(53)n∑n=1∞1n НеверноВопрос 8Частично правильныйБаллов: 0,500 из 1,000Не отмеченоОтметить вопросТекст вопросаДля ряда ∑n=1∞un с положительными членами, для которого выполнено условие limn→∞un+1un=k,k=const , справедливы утвержденияВыберите один или несколько ответов:k=25;limn→∞un=0k=13;ряд∑n=1∞un сходится Верно

---

Смотрите также файлы

• Упражнения на быстроту и ловкость. Челночный бег 10 х10 м.docx

• Основные виды и функции торговых посредников.pdf

• 35 главные проблемы совершенствования биологического образования в современной школе.pdf

• Методические рекомендации и материалы по проведению итоговой государственной аттестации по истории узбекистана для учащихся 11 классов общеобразовательных.pdf

• Бизнес планИгровое пространство PlayStation club gg good Games.pdf