В качестве критерия проверки гипотезы используется случайная величина:

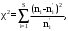(3.1)

Где n'_i- теоретические частоты, n_i-эмпирические частоты. Определение теоретических частот может производиться согласно предыдущему способу.

Установлено, что при n→∞ по закон распределения случайной величины независимо от закона распределения результатов измерений, стремится к закону степенями свободы k = S-1-r, где S – число частичных интервалов, г- число параметров предполагаемого распределения. Для нормального распределения в общем случае r = 2 (оценивают математическое ожидание и среднее квадратическое отклонение), соответственно k = S– 3.

Вычислив χ² и определив k, по таблице распределений χ² в зависимости от выбранного значения уровня значимости α =1– P (P-Доверительная вероятность) находятся границы χ² (k; ɑ) и χ² (k; 1 – α). Если выполняется условие χ² (k; α) < χ² < χ2 (k:1 – α), то эмпирическое распределение не противоречит теоретическому с вероятностью Р.

Сначала найдём частоты эмпирического распределения:

1. 
   Расположим результаты измерения в порядке возрастания:
   

47,58 48,15 48,45 48,50 48,56 48,95 49,71 49,79 49,79 51,77 52,12 52,41 52,81 52,97

2. 
   Диапазон изменения значений результатов измерений разбивается на r интервалов по формуле Стерджесса
   

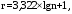(3.2)

3. 
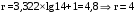
   Ширина интервалов
   

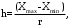(3.3)

4. 
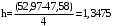
   Определяются границы интервалов так, чтобы верхняя граница j-го интервала была равна: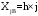 , а его нижняя граница совпадала с верхней границей (j-1)-го интервала: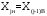
   

;

;

;

;

;

;

;

---

;

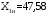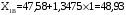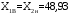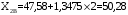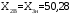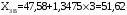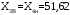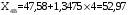
5. 
   Определяется число результатов измерений, попавших в заданный j-й интервал по условию X_jН < Xi ≤ X_jВ. Числа результатов измерений nj называют частотами, а их отношения к общему числу результатов измерений относительными частотами
   
6. 
   Найдем середины интервалов и относительные частоты:
   

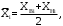(3.4)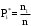

, (3.5)

;







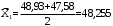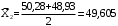
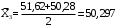
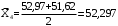
Таблица 2- Результаты расчетов эмпирической частоты

Номер интервала	Граница интервала			Частота		Серединный интервал		Относительные частоты
	Xн	Xв
1	2	3	4		5		6
1	47,58	48,93	5		48,255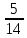
2	48,93	50,28	4		49,605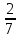

Продолжение таблицы 2

1	2	3	4	5	6
2	48,93	50,28	4	49,605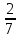
3	50,28	51,62	0	50,952	0
4	51,62	52,97	5	52,297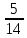

---

Потом находим теоретические частоты:

1. 
   Определим параметры предполагаемого (теоретического) нормального закона распределения.
   

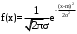, (3.6)

Оценку математического ожидания найдем по формуле

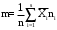, (3.7)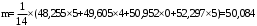



Оценку дисперсии вычислим по формулам

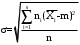, (3.8)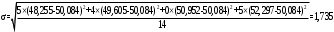

2. 
   Переходим к новой переменной Zi и вычисляют концы интервалов
   

При этом наименьшее значение, т. е.X_Н1, полагаем равным ∞, а наибольшее, т. е. X_В4, полагаем равным +∞.

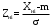, (3.9)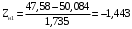









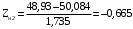
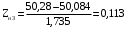
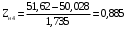
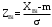, (3.10)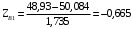









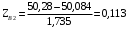
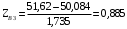
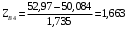
Таблица 3-Результаты расчётов интервалов с переменной Zi

Номер интервала	Zнi	ZВi
1	-∞	-0,665
2	-0,665	0,113
3	0,113	0,885
4	0,885	+∞

3. 
   Выполним расчет теоретических частот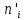 по формуле . Для вычисления вероятностей P_i по формуле воспользуемся таблицей Лапласа Приложения со значениями нормальной стандартной функции распределения.
   

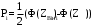, (3.11)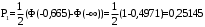

---

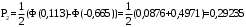
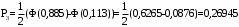
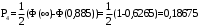
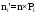, (3.12)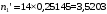

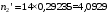
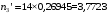
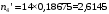
4. 
   По формуле (3.1) найдём значение χ²
   

5. 
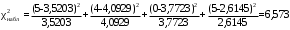
   По таблице квантилей распределения χ² (см. таблицу в Приложения) с числом степеней свободы k = 4– 3= 1 находим, что χ²_табл = 6,635 для α =1– 0,99=0,01 и χ² _табл = 0,00016 для α=0,99.
   
6. 
   Поскольку (0,00016 < 6,573 < 6,635), то можно считать, что гипотеза о нормальном законе распределении измерений растровым электронным микроскопом строки нанообъекта не противоречит теоретическому нормальному закону распределения с вероятностью Р = 0,99.
   

ЗАКЛЮЧЕНИЕ

В настоящее время аппаратура и методы растровой электронной микроскопии применяются практически во всех естественнонаучных исследованиях и для контроля в условиях производства. Развитие полупроводниковой микро-, нано-, оптоэлектроники стимулировало появление и развитие новых методов растровой микроскопии, основанных на таких явлениях, как генерация, диффузия, рекомбинация электронно-дырочных пар, полевая зависимость вторичных электронов и др.

Помимо традиционного применения растровой электронной микроскопии как метода наблюдения и получения изображения исследуемого объекта с большим увеличением и высоким разрешением он становится методом, позволяющим получить количественную информацию об электрофизических, геометрических параметрах, параметрах реальной кристаллической структуры, фазовом и химическом составе, структуре энергетических уровней и т.д.

Популярность и широкое применение растровой электронной микроскопии обусловлены совокупностью уникальных возможностей, присущих этому методу: получение трехмерных изображений широкого спектра материалов с большой глубиной фокуса 9, простотой применения 10, высокая скорость получения изображения «области интереса» и проведения качественного и количественного анализа химического состава образца 11, высоким пространственном разрешением

---

, достигающее 1 нм 12, использование различных детекторов, значительно расширяющих диапазон получаемых данных 13, 14,15.

Поэтому, поставленная цель курсовой работы - изучение использования растровой электронной микроскопии в нанометровом и микрометровом масштабе, на сегодняшний день является актуальной и необходимой.

В ходе написания курсовой работы были рассмотрены следующие задачи, связанные с изучением физических основ растровой электронной микроскопии, проанализирован принцип работы основных блоков растрового электронного микроскопа, изучены особенности конструкции растрового электронного микроскопа. На основании полученных результатов измерений растровым электронным микроскопом строки нанообъекта выполнена идентификация функции распределения результатов измерения.

Современный РЭМ — это сложный прибор высокого технического уровня, включающий несколько основных систем: электронно-оптическую систему, позволяющую получить разрешение вплоть до 10Å при токах электронного пучка 10^-11–10^-12 Å; вакуумную систему, обеспечивающую вакуум 2×10^-6 торр; систему детектирования различных сигналов с малошумящим многоканальным усилительным трактом; прецизионную механическую систему перемещения объекта; систему сбора и обработки информации с визуализацией и фотографированием изображения. Конструкция РЭМ оснащается спектрометрами с дисперсией по длинам волн и по энергиям для реализации метода рентгеноспектрального микроанализа, устанавливается устройство сбора и вывода катодолюминесцентного излучения 16.

В процессе выполнения курсовой работы была выполнена проверка соответствия эмпирического распределения результатов измерений растровым электронным микроскопом строки нанообъекта нормальному теоретическому закону распределения на основе критериев согласия Пирсона.

Для этого был выполнен расчет частот теоретического и эмпирического распределения. В результате расчетов было получено расчетное значение критерия Пирсона. Расчетный критерий для нормального распределения составил χ²_набл = 6,573 при количестве степеней свободы 1. Табличное значение критерия Пирсона равно χ²_табл = 6,635. По таблице квантилей распределения χ² с числом степеней свободы k = 4– 3= 1 были определены границы: χ²_табл = 6,635 для α =1– 0,99=0,01 и χ²_табл = 0,00016 для α=0,99.

Так как выполняется условие χ²_табл(k,α) ≤ χ²_набл ≤ χ²_табл

---

Смотрите также файлы

• Новгородская икона Спас Нерукотворный.docx

• Гражданская война в России основные причины и последствия.docx

• 1 Верно Баллов 1,00 из 1,00 Отметить вопрос Текст вопроса Архитектор Исаакиевского Собора Выберите один ответ a. К. И. Росси b. Л. И. Шестов c. А. Н. Воронихин d. А. А. Монферран Вопрос 2.docx

• Темам 3, 4.docx

• Занятие 1 Задание Продолжите высказывания, аргументируя свою точку зрения.docx