МКОУ Аносовская СОШ


План-конспект урока

по алгебре и начала математического анализа

в 10 классе МКОУ Аносовская СОШ

на тему «Равносильность неравенств»

Разработал: Фалеева Галина Васильевна

слушатель курсов профессиональной переподготовки «Учитель математики: Преподавание математики в образовательной организации»

Аносово 2022
Тема урока: Равносильность неравенств

Дата проведения: 25.10.22

Тип урока: комбинированный

Цель урока.

Образовательная: ввести понятие иррационального неравенства, «открыть» теоремы о равносильности уравнений, научить решать простейшие иррациональные неравенства.

Развивающая: развитие познавательного интереса учащихся, самостоятельного мышления, навыков правильной речи.

Воспитательная: положительный интерес к изучению математики, ответственность, осознание общечеловеческих ценностей.
Задачи:

- организация взаимодействия, формирование умения работать с новой информацией по теме;

-усвоение знаний , умений, навыков;

-развитие способностей, опыта творческой деятельности

Планируемые образовательные результаты.

Личностные:

- Осознание учащимися ценности полученных знаний.

- Умение провести самооценку и взаимооценку.

- Формирование этических норм поведения, уважения к труду

Межпредметные:

- Умение применять и сохранять цель урока.

- Умение находить способы решения поставленной цели.

- Умение слушать собеседника и вести диалог, высказывать свою точку

зрения, правильно говорить.

Предметные:

- Формирование навыка решения неравенств с одной переменной методом

интервалов.

- Умение применять полученные знания при решении задач.
Оборудование 1. Компьютер;

2. Проектор;

3. Экран;

4. Тетради, ручки, линейки.
План урока

Ход урока	Деятельность учителя	Деятельность учащихся
1.Организа-ционный этап (1м)	приветствует учащихся отмечает в журнале отсутствующих проверяет готовность к уроку	Готовятся к уроку (достают тетради, ручки). Готовятся к восприятию материала.
2.Этап контроля полученных ранее знаний: Фронтальный опрос : (9м)	фронтальный опрос, Устанавливает правильность, полноту и осознанность ответов на вопросы	Отвечают на вопросы, дополняют отдельные ответы, если в этом есть необходимость
3.Этап формулирования темы урока (2м)	постановка целей и задач через решение поставленной проблемы.	Коллективная работа .
4. Изучение нового материала. (15м)	Объясняет новый материал, проводит беседу, дает пояснения, задает вопросы проблемного характера..	Работа в группах, коллективная работа. Конспектируют. Принимают участие в беседе. Отвечают на вопросы учителя и уточняют непонятные вопросы.
5. Решение экспериментальных задач (10м)	выдает задание и проверяет работу учеников	работа в группах, коллективная работа Решение задач на применение формул
6.Обобщение темы урока и первичный контроль знаний. (2м)	Фронтальный опрос,	Отвечают на вопросы
7. Оценочный этап. (1м)	Обобщает изученное. Характеризует и оценивает работу учащихся на уроке, с учетом активности в течение занятия.	Выражают свои мысли о том, что они узнали на занятии, быстро и чётко высказываются
8.Домашнее задание. (1м)	Объясняет суть домашнего задания.	Записывают домашнее задание
9. Рефлексия (1м) .	Просит оставить отзыв и благодарит за урок	Обучающиеся заполняют анкету

---

Ход урока:

1. 
   Организационный этап: приветствие обучающихся, отметка отсутствующих в журнале, положительный настрой на работу,
   
2. 
   Этап контроля полученных ранее знаний: 1) Какой раздел мы с вами изучаем? (Степенная функция): 2) Какие вопросы мы рассматривали на последних уроках? (Степенная функция, ее свойства и графики, взаимно обратные функции, равносильные уравнения и неравенства, иррациональные уравнения)
   

На сегодняшнем уроке мы с вами продолжим изучение нашей темы. Но сначала давайте немного повторим основные понятия формулы и определения.

Фронтальный опрос:

1 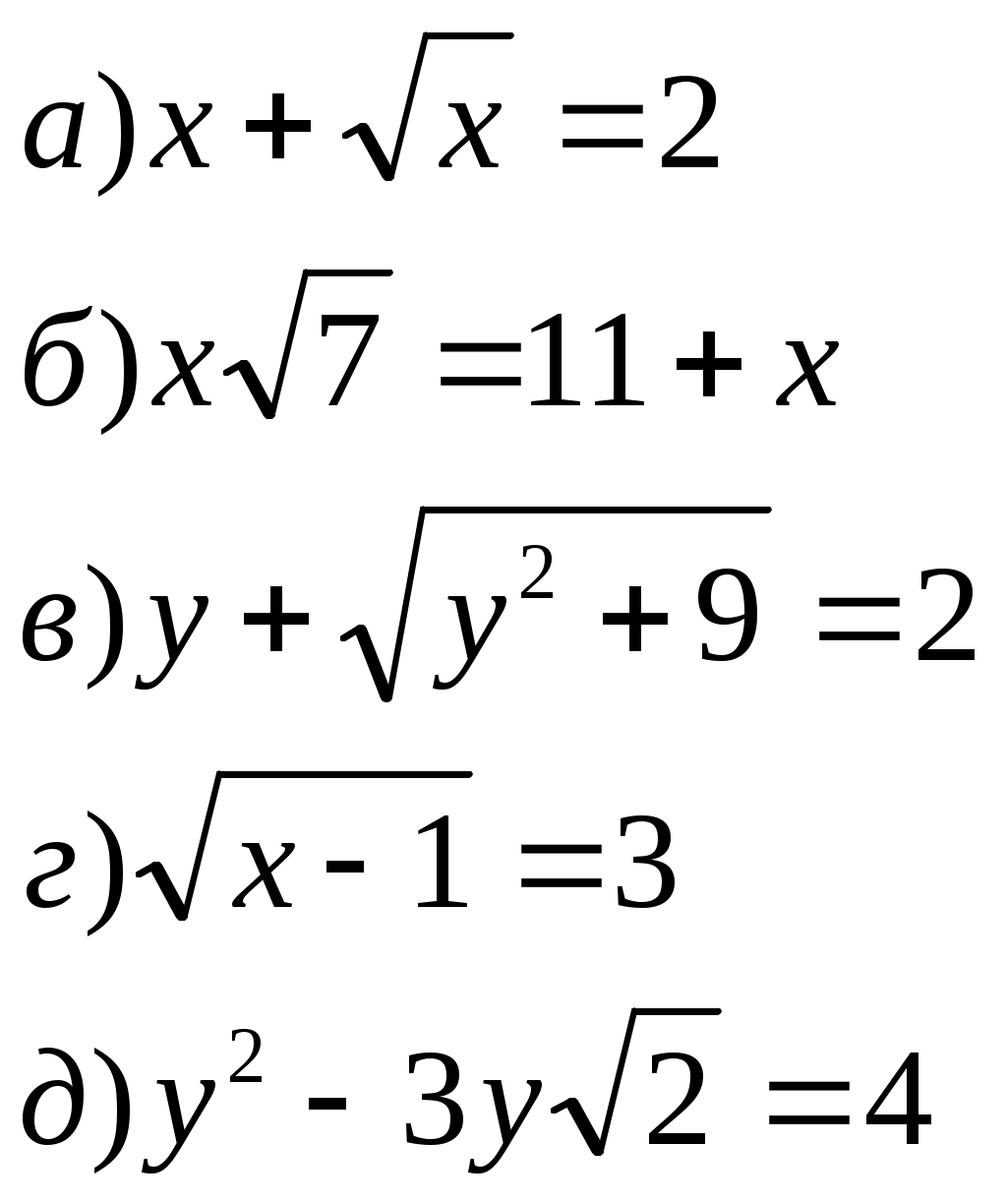. Какие уравнения называются иррациональными? (В уравнениях, в которых неизвестная переменная х находится под знаком корня, называются иррациональными уравнениями.) 2. Какие из следующих уравнений являются иррациональными


(Уравнения под пунктами а, в, г являются иррациональными уравнениями, так как неизвестные переменные находятся под знаком корня.)

3 .Какие уравнения называются равносильными? (если они имеют одинаковые корни или если оба уравнения не имеют корней..) 4. Вспомните определение решения неравенства. (Решением неравенства называется всякое действительное значение неизвестного, при котором неравенство справедливо. Решить неравенство — значит найти множество всех его решений. Это множество может оказаться пустым, т. е. существуют неравенства, которые не имеют решений.)

3.Этап формулирования темы урока:

Учитель вместе с учащимися формулирует цели и задачи урока. Здесь мы сначала дадим определение равносильных неравенств и приведем примеры. Дальше перечислим основные виды равносильных преобразований неравенств и докажем их. А в заключение выясним, почему при решении неравенств нужно использовать только равносильные преобразования.
4.Изучение нового материала.

Выполнение некоторых действий с правой и/или левой частью неравенства или с их отдельными слагаемыми может давать новые неравенства, имеющие те же решения, что и исходное неравенство. Замену исходного неравенства на новое равносильное ему неравенство при помощи таких действий назвали равносильным преобразованиям неравенства. Равносильное преобразование неравенства – это его замена другим равносильным ему неравенством, то есть, неравенством, имеющим то же множество решений. Сами преобразования, приводящие к равносильному неравенству, также называют равносильными преобразованиями.

---

Возникает логичный вопрос: «Зачем вообще нужны эти равносильные преобразования неравенств»? Например, они позволяют решать неравенства: с их помощью от решения исходного неравенства можно перейти к решению более простого, но равносильного неравенства (далее учащиеся записывают определения в тетради).

Определение 1.Два уравнения с одной переменной

f(х) = g(х) и р(х) = h(х) называют равносильными, если множества их корней совпадают.
Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
Например, уравнения х²- 4 = 0 и (х + 2)(2^x - 4) = 0 равносильны, оба они имеют по два корня:

2 и -2. Равносильны и уравнения х²+1=0и√x=-3, поскольку оба они не имеют корней.
Определение 2.Если каждый корень уравнения

f(x) = g(х) ₍₁₎

является в то же время корнем уравнения

р(х) = h(х), (2)

то уравнение (2) называют следствием уравнения (1).
Например, уравнение х - 2 = 3 имеет корень х = 5, а уравнение (х - 2)² = 9 имеет два корня: х₁= 5, х₂= -1. Корень уравнения х - 2 = 3 является одним из корней уравнения (х - 2)² = 9. Зна­чит, уравнение (х - 2)² = 9 — следствие уравнения х - 2 = 3.

Достаточно очевидным является следующее утверждение.
Два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.

Рассмотрим некоторые из равносильных преобразований:

1. 

2. 

3. 

4. 

5. 

6. 
Ответим на вопрос о том, когда уравнение теряет корни и как этого недопустить ?

Существует несколько причин потери корней:

а) деление обеих частей уравнения на одно и тоже выражение в случае, когда оно может принимать значение равное 0; так при решении уравнения необходимо переходить к уравнению (а не к уравнению ).

---

б) сужение ОДЗ в процессе решения уравнения; это, например, происходит при использовании некоторых тригонометрических формул.

 при переходе к уравнению-следствию (не важно, какое преобразо­вание при этом проводилось) не надо искать ОДЗ, но надо знать, что проверка найденных корней явля­ется обязательным элементом решения уравнения.

Подводя итог, можно сказать, что при переходе к уравнению, равносильному исходному на некотором множестве М, проверка найденных корней подстановкой их в исходное уравнение не является необходимым элементом решения, но надо обязательно отобрать из всех полученных корней те, которые принадлежат множеству М.
Неравенство 3x2+3,6x≤0,84  равносильно неравенству  3x2+3,6x−0,84≤0,

0,84 перенесли из правой части неравенства в левую с противоположным знаком;

 

Неравенство  4x2−14x+12≥0  равносильно неравенству 2x2−7x+6≥0,
  обе части первого неравенства разделили на положительное число 2;


Неравенство  −2x2+7x−6>0 равносильно неравенству 2x2−7x+6<0, 

обе части первого неравенства умножили на отрицательное число −1,

при этом знак неравенства > изменили на противоположный, т.е. <;


Неравенство  (2t2+3)(7t−6)>0  равносильно неравенству  7t−6>0, 
обе части исходного неравенства разделили на выражение 2t2+3,

положительное при любых значениях t, при этом знак исходного неравенства оставили без изменения

5. Решение экспериментальных задач

Пример 1.

Решим уравнение: 

Возведем в квадрат обе части уравнения, получим:

, которое не будет равносильно исходному уравнению, потому что у этого уравнения два корня  , а у первоначального уравнения только один корень х=4.

Пример 2.

1. 
   Неравенства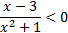   и x-3<0 равносильны, так как имеют одно и то же множество решений x<3.
   
2. 
   Неравенства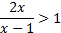   и 2x>x-1 не равносильны, так как решениями первого являются числа x<-1 и x>1, а решениями второго- числа x>-1. При решении неравенств обычно данное неравенство преобразуется в ему равносильное.
   

---

Пример 3.

Неравенства

Решение. На сей раз обе части неравенства всегда неотрицательны, так что возведение в квадрат дает неравенство, равносильное исходному на его естественной области определения. Возведение в квадрат дает неравенство:  , область определения дает неравенства:  и 

6.Обобщение темы урока и первичный контроль знаний. 1. Что называется корнем (или решением) уравне­ния с одной переменной (называется значение переменной, при подста­новке которого в уравнение получа­ется верное равенство) 2. Что значит решить уравнение ( значит най­ти все его корни (и обосновать, что других корней нет) или доказать, что корней нет). 3. Как получить уравнение, равносильное заданному (надо из одной части уравнения пе­ренести в другую слагаемые с про­тивоположным знаком). 4. Если из правильности первого равенства следует правильность каждого последую­щего, то это? ( уравнения-следствия).

7. Оценочный этап.

Выставление оценок за урок.

8.Домашнее задание: по учебнику с. 54-58 выучить расчетные формулы, определения решить №144 и 147.

9.Рефлексия. Дорогие, друзья! Наш урок подошел к концу. Оставьте ваши отзывы об уроке.

Обучающиеся заполняют анкету (Приложение 1).

Всем спасибо за урок! Желаю Вам успехов на других занятиях.

Литература:

1. 
   Алгебра и начала математического анализа. 10 класс: учеб. Для общеобразоват. Учреждений: базовый и углубленный. уровни [Ш. А. Алимов, М. Ю. Колягин, М.В.Ткачева, Н. Е. Федорова, М. И. Шабунин]; –8–е изд. – М.: Просвещение, 2020. – 3463с.
   
2. 
   Алгебра и начала анализа. 10 класс : поурочные планы по учебнику Ш. А. Алимова и др. 1 полугодие / авт.–сост. Г. И. Григорьева. –Волгоград: Учитель, 2008. –150 с.
   

Приложение 1.

Заполните анкету, подчеркните ответ, наиболее соответствующий Вашему.

1.На уроке я работал 2.Своей работой на уроке я 3.Урок для меня показался 4.За урок я 5.Мое настроение 6.Материал урока мне был 7.Домашнее задание мне кажется

активно / пассивно доволен / не доволен коротким / длинным не устал / устал стало лучше / стало хуже понятен / не понятен полезен / бесполезен интересен / скучен легким / трудным

---

Смотрите также файлы

• Сабаты таырыбы Аспан денелері туралы ылым Малімні атыжні Жолдас Камила.docx

• Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа с. Мичурино Ардонского района.pdf

• Спецификация итоговой контрольной работы за курс географии 5 класса.docx

• Ктп предмету Цифровая грамотность для 1 класса.docx

• Сынып 7 А сынып.docx