ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 51
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание №4. Закон распределения и числовые характеристики дискретных случайных величин
1) Изделия в количестве 3 штук испытываются при перегрузочных режимах. Вероятность для каждого изделия пройти испытание равна 4/5. Найти функцию вероятности случайного числа Х изделий, выдержавших испытание. Найти М(Х) и D(Х).
2) Стрелок ведёт стрельбу по мишени до первого попадания, имея боезапас 4 патрона. Вероятность попадания при каждом выстреле равна 0,6. Построить функцию распределения боезапаса, оставшегося неизрасходованным. Найти М(Х) и D(Х).
3) Производятся независимые испытания, в каждом из которых с вероятностью 0,8 может произойти некоторое событие А, общее число испытаний не превосходит четырёх. Построить функцию распределения случайной величины Х числа испытаний. Найти М(Х) и D(Х).
4) Производится 4 независимых опыта, в каждом из которых вероятность появления события А равна 0,3. Построить функцию распределения числа Х появления события А. Найти М(Х) и D(Х).
5) Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить функцию распределения числа Х выбитых очков. Найти М(Х) и D(Х).
6) Из партии, содержащей 100 изделий, среди которых 10 дефектных, выбраны случайным образом 3 изделия для проверки качества. Построить функцию распределения случайного числа Х дефектных изделий в выборке. Найти М(Х) и D(Х).
7) Производится три броска мяча в корзину. Вероятность попадания в корзину при каждом броске равна 0,3. Построить функцию распределения случайного числа Х попаданий мяча в корзину. Найти М(Х) и D(Х).
8) Из урны, в которой лежат 5 чёрных и 3 белых шара, последовательно вынимают шары до тех пор, пока не появится чёрный шар. Найти функцию распределения случайного числа Х вынутых при этом белых шаров, т.е. числа белых шаров, вынутых до первого чёрного шара. Найти М(Х) и D(Х).
9) Из урны, в которой лежат 5 чёрных и 3 белых шара, вынимают 4 шара. Построить функцию распределения случайного числа Х вынутых белых шаров. Найти М(Х) и D(Х).
10) Два баскетболиста поочерёдно бросают мяч в корзину до тех пор
, пока один из них не попадёт, но не более трёх раз. Построить функцию распределения случайного числа бросков, производимых каждым из баскетболистов, если вероятность попадания для первого из них равна 0,4, а для второго – 0,6. Найти М(Х) и D(Х).
11) Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все 4 патрона). Построить функцию распределения случайного числа Х израсходованных патронов при условии, что вероятность попадания при каждом выстреле равна 0,8. Найти М(Х) и D(Х).
12) Стрелок делает 3 выстрела по мишени. Вероятность попадания при каждом выстреле равна 2/3. Построить функцию распределения случайного числа Х попаданий. Найти М(Х) и D(Х).
13) Игральная кость бросается 3 раза. Построить функцию распределения для возможного числа Х выпадений "шестёрки". Найти М(Х) и D(Х).
14) В стопке тетрадей находятся 6 тетрадей в клетку и 3 тетради в линию. Наудачу взяты 3 тетради. Построить функцию распределения случайного числа Х тетрадей в линию в отобранной группе. Найти М(Х) и D(Х).
15) Вероятность детали быть бракованной равна 1/5. Взято на пробу 3 детали. Построить функцию распределения для случайного числа Х бракованных изделий в пробе. Найти М(Х) и D(Х).
16) Баскетболист производит 3 броска мячом в корзину с вероятностью попадания при каждом броске 0,6. Каждое попадание приносит команде 2 очка. Построить функцию распределения для возможного числа Х очков, принесённом баскетболистом команде. Найти М(Х) и D(Х).
17) В коробке 3 красных и 2 синих карандаша. Производится вынимание до появления синего карандаша. Построить функцию распределения случайного числа Х выниманий. Найти М(Х) и D(Х).
18) Из большой партии изделий взяли на проверку 4 детали. Доля дефектных деталей во всей партии 20%. Построить функцию распределения для случайного числа Х дефектных деталей в пробе. Найти М(Х) и D(Х).
19) Три орудия делают один залп по общей цели. Вероятность попадания в цель для первого орудия равна 0,6, для второго – 0,8, для третьего 0,7. Построить функцию распределения для случайного числа Х попаданий в цель при залпе. Найти М(Х) и D(Х).
20) Карточки с цифрами 1, 2, 3, ,4 ,5 перемешаны, а затем случайным образом вынимаются до появления чётной цифры. Построить функцию распределения для случайного числа Х выниманий. Найти М(Х) и D(Х).
21) На месте происшествия оказались 6 женщин и 4 мужчины. Для составления протокола случайным образом отобраны 4 человека. Построить функцию распределения для случайного числа Х мужчин, вошедших в группу для составления протокола. Найти М(Х) и D(Х).
22) Монета бросается до появления "герба" но не более 5 раз. Построить функцию распределения для случайного числа Х бросаний (т.е. числа бросаний до первого появления "герба"). Найти М(Х) и D(Х).
23) На пути движения автомашины 4 светофора, на которых с равной вероятностью может быть разрешающий или запрещающий сигнал. Построить функцию распределения для возможного числа Х остановок автомашины у светофора. Найти М(Х) и D(Х).
24) На остановке стояли четверо мужчин и три женщины. В подошедшее такси случайным образом сели четыре человека. Построить функцию распределения для случайного числа Х женщин, севших в такси. Найти М(Х) и D(Х).
25) Игрок А играет с игроком В либо до первого выигрыша игрока А либо 4 партии. Составить функцию распределения для случайного числа Х игр, если вероятность выигрыша игрока А равна 0,6. Найти М(Х) и D(Х).
26) Вероятность того, что в библиотеке необходимая курсанту книга свободна, равна 0,3. Составить функцию распределения случайного числа Х библиотек, которые посетит курсант в поисках книги, если в городе 4 библиотеки.
27) Три стрелка стреляют по одной цели. Вероятность попадания в цель для первого стрелка равна 0,5, для второго – 0,7, для третьего – 0,4. Составить функцию распределения для случайного числа Х попаданий в цель при одном залпе. Найти М(Х) и D(Х).
28) Испытывается устройство, состоящее из трёх независимо работающих приборов. Вероятности отказа работы приборов таковы: р1 = 0,3; р2 = 0,4; р3 = 0,5. Составить функцию распределения для случайного числа Х отказавших приборов. Найти М(Х) и D(Х).
29) Монета бросается 4 раза. Построить функцию распределения случайного числа Х выпадений "герба". Найти М(Х) и D(Х).
30) В ящике 7 белых и 3 чёрных шара. Наугад вынуто 3 шара. Составить функцию распределения для случайного числа Х чёрных шаров в отобранной партии. Найти М(Х) и D(Х).
Задание №5. Функции распределения и числовые характеристики непрерывных случайных величин
1) Случайная величина X задана плотностью распределения вероятностей:
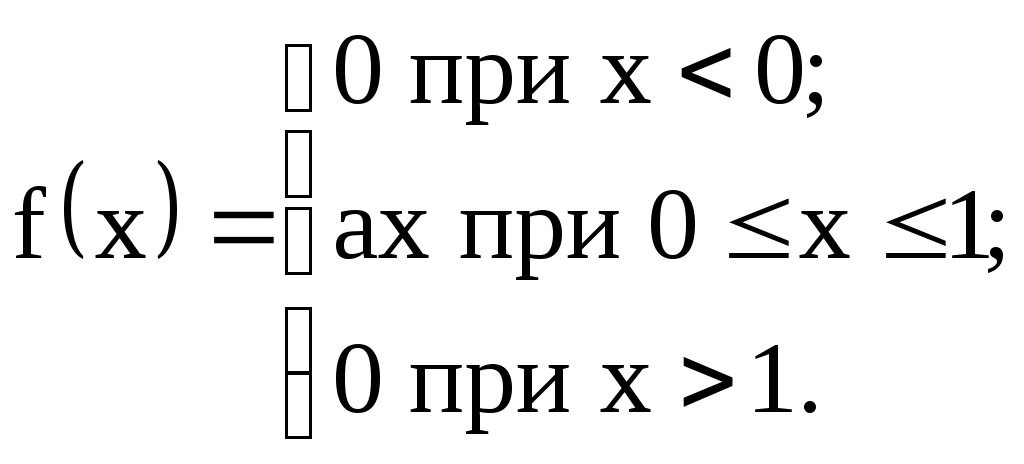
Найти коэффициент "а", F(x), M(X), D(X),
.
2) Дана функция f(x) = axe-кx (к > 0), (
3) Случайная величина Х задана интегральной функцией распределения:
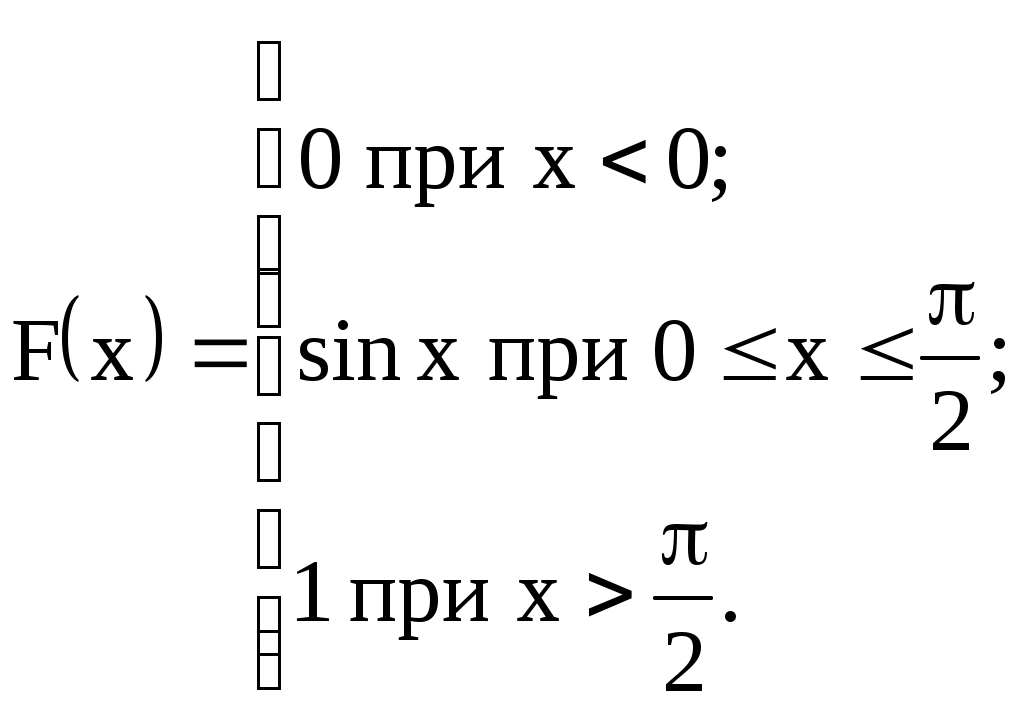
Найти М(Х), D(Х).
4) Случайная величина задана плотностью распределения:
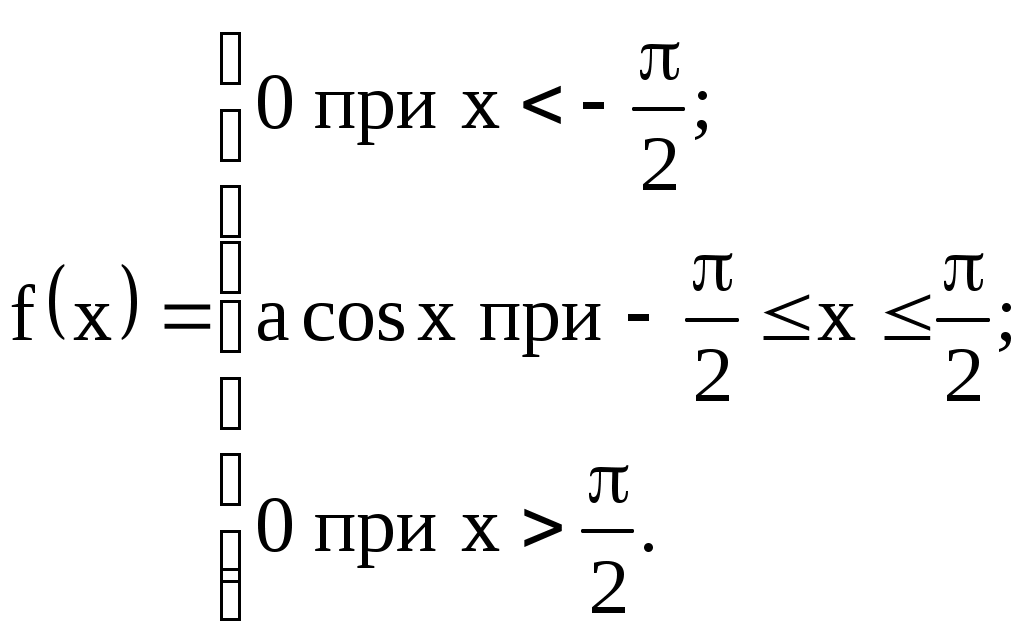
Найти коэффициент "а", F(x), M(X), D(X).
5) Функция распределения случайной величины Х задана выражением:
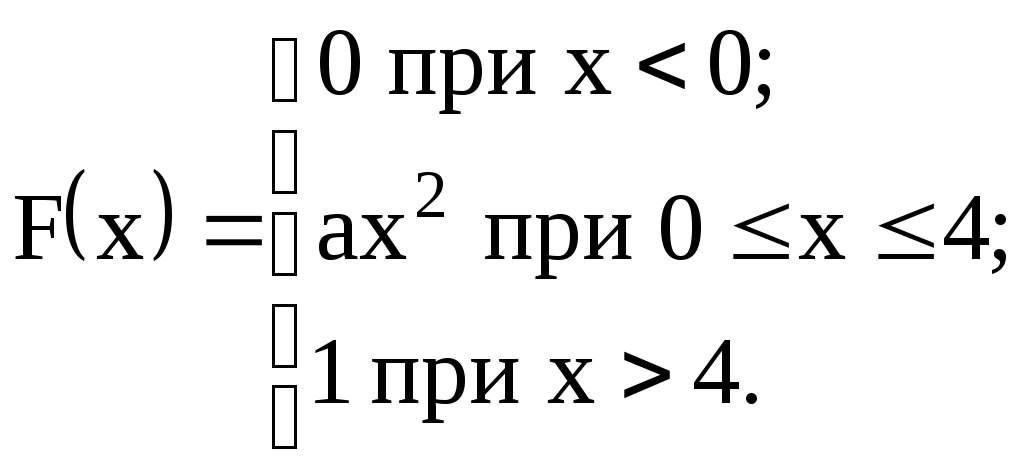
Найти коэффициент "а", M(X), D(X),
6) Дана интегральная функция распределения случайной величины Х:
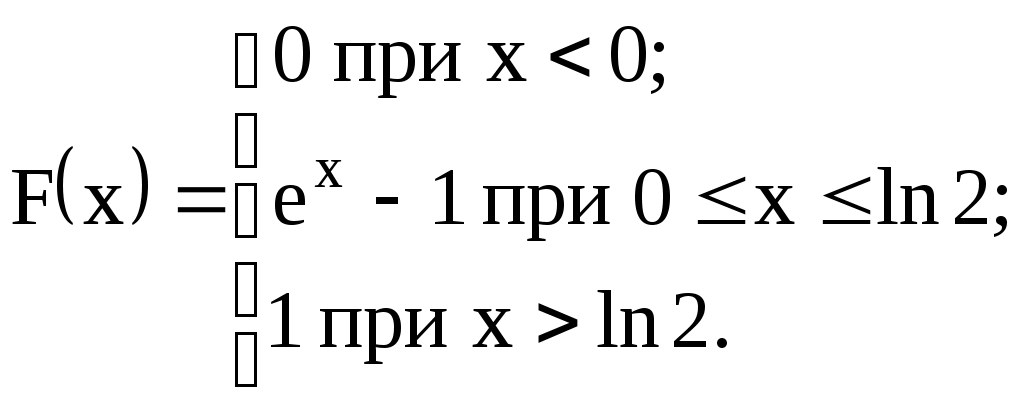
Найти M(X) и D(X).
7) Дана интегральная функция распределения случайной величины Х:
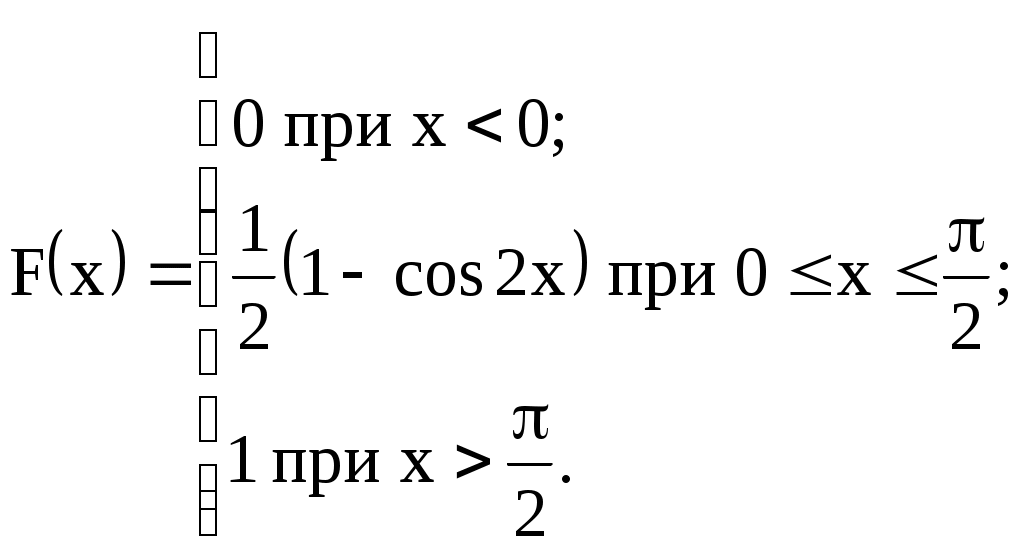
Найти M(X), D(X),
8) Дана функция плотности распределения случайной величины Х:
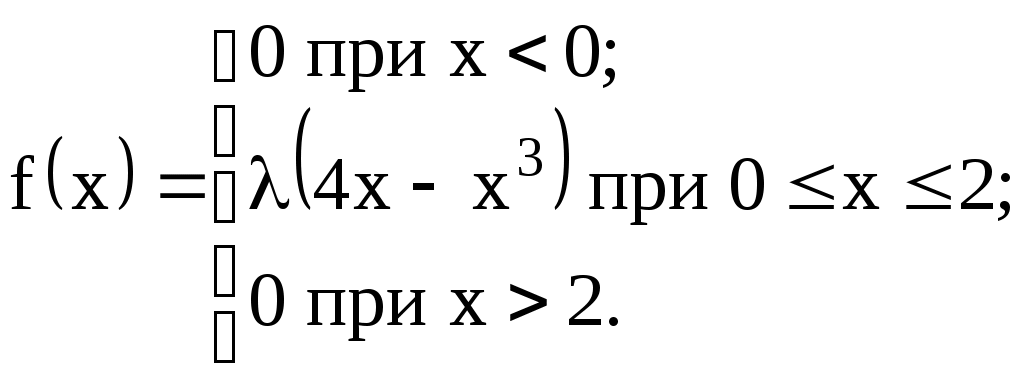
Найти значение "", M(X), D(X),
| Дана интегральная функция распределения случайной величины Х | Найти |
| 9) 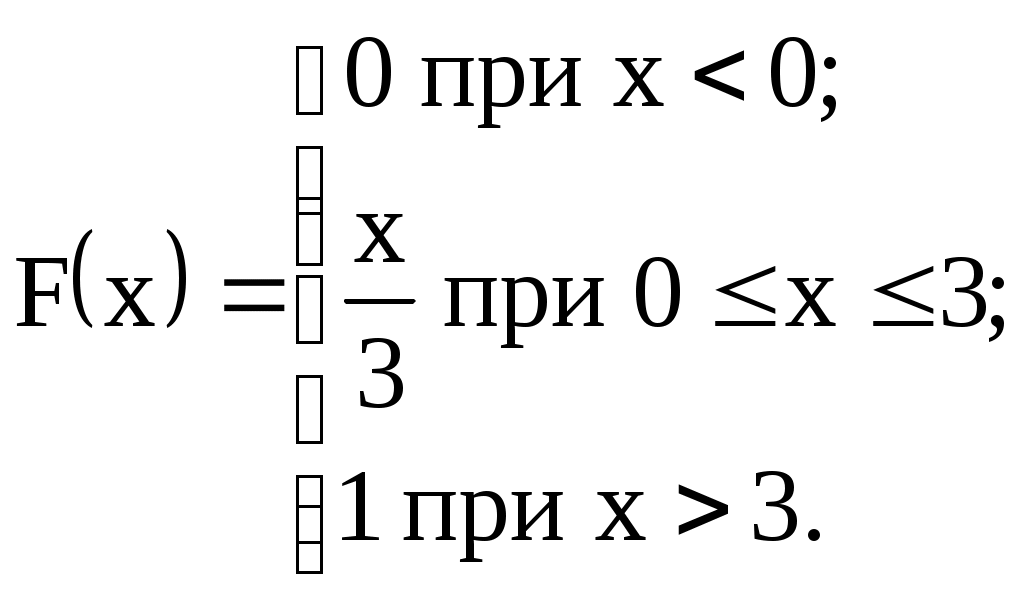 | M(X), D(X), |
| 10) 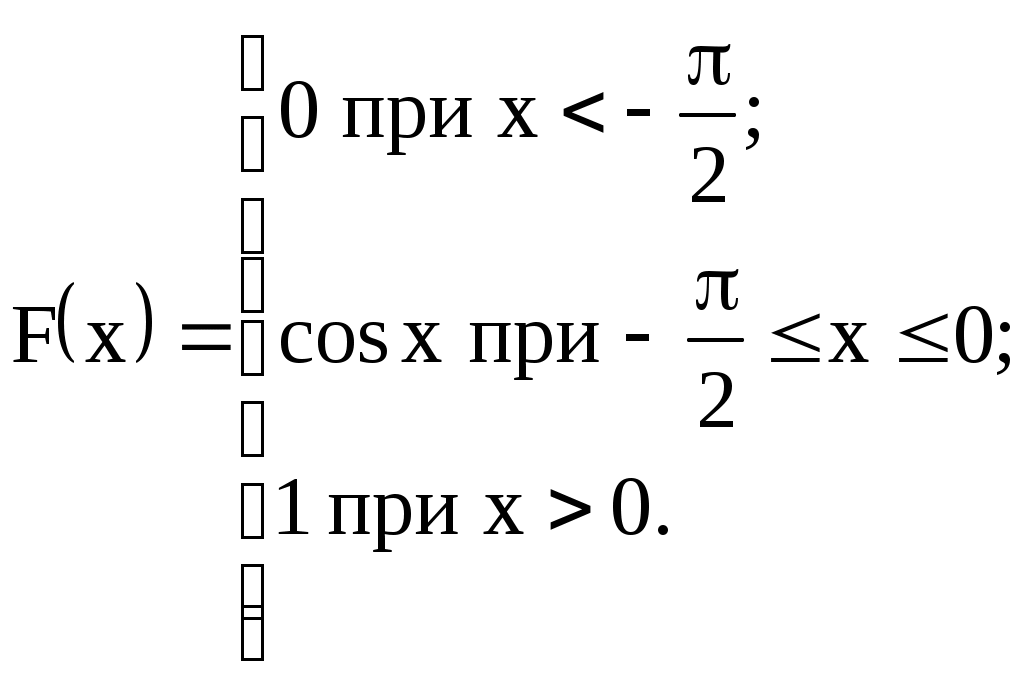 | M(X), D(X), |
| 11) 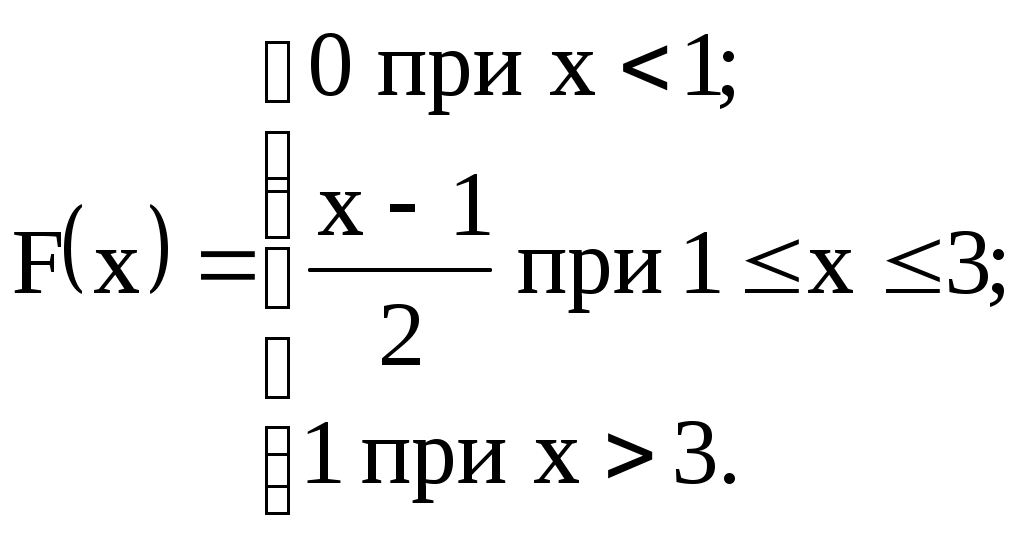 | M(X), D(X), |
| 12) 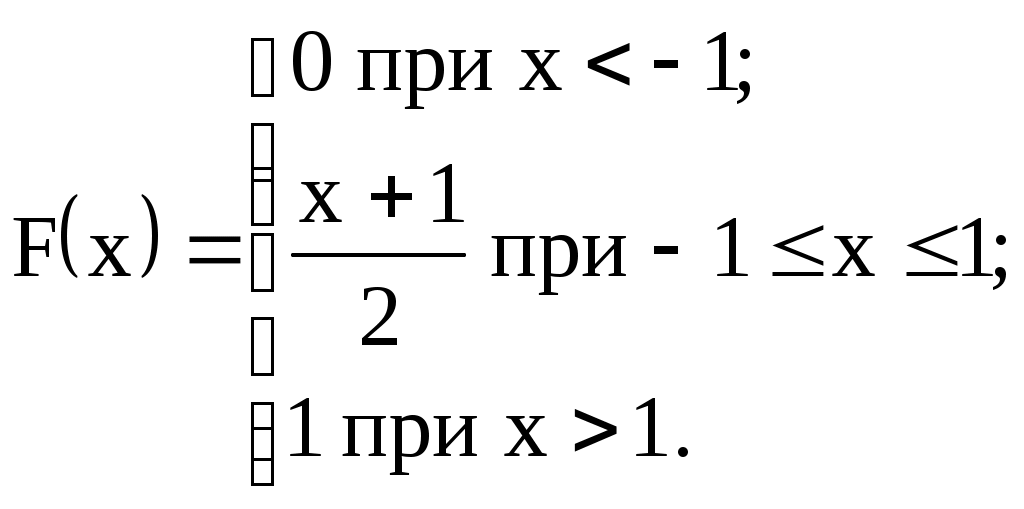 | M(X), D(X), |
| 13) 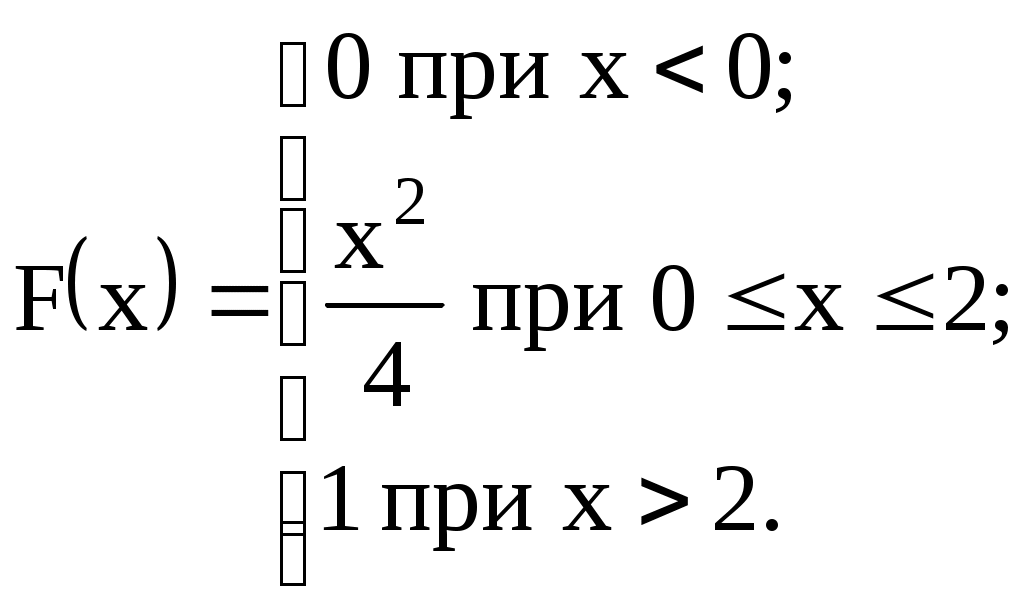 | M(X), D(X), |
| 14) 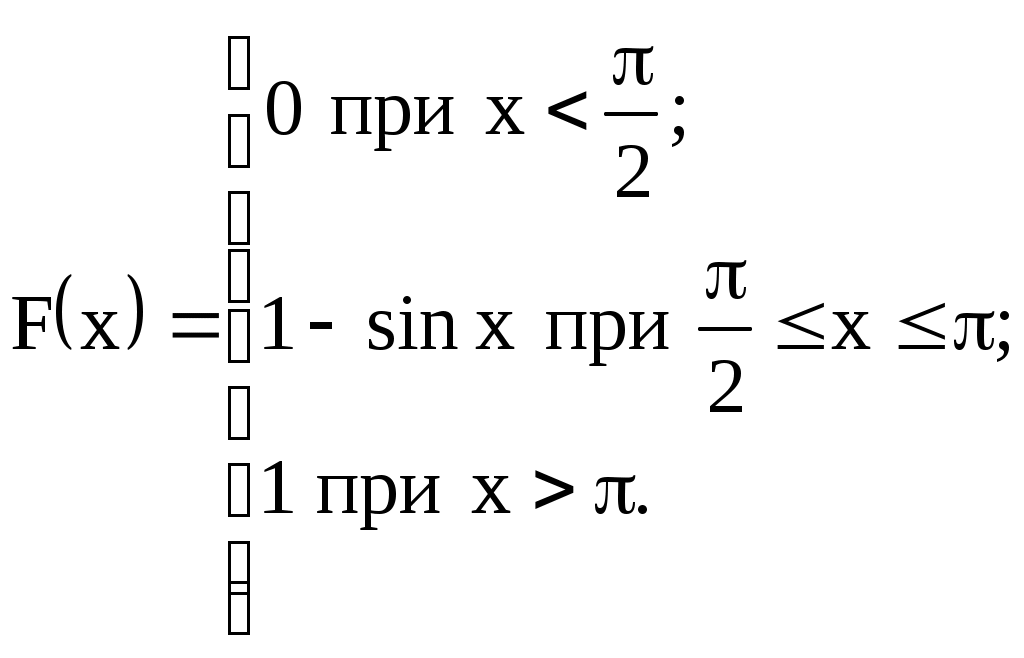 | M(X), D(X), |
| Дана интегральная функция распределения случайной величины Х | Найти |
| 15) 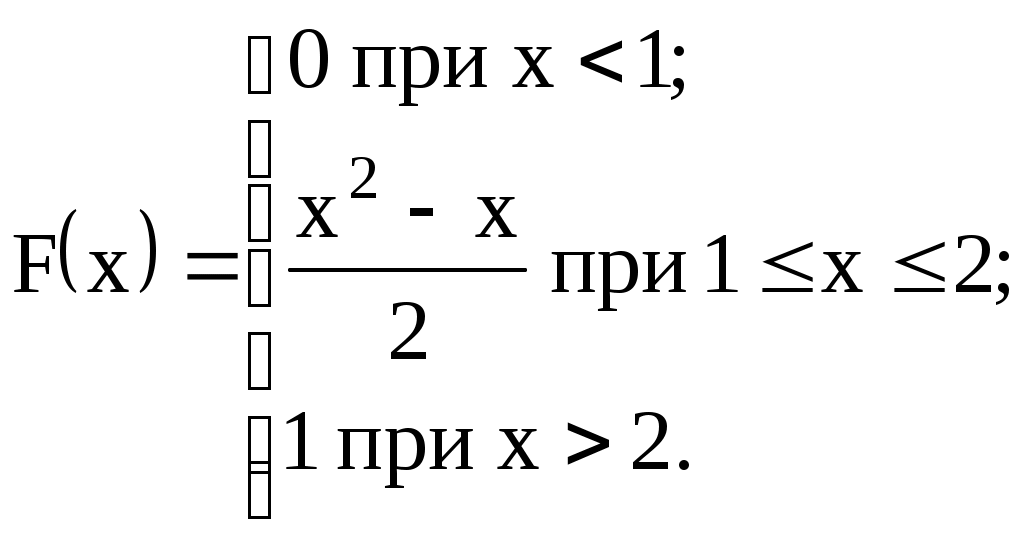 | M(X), D(X), |
| 16) 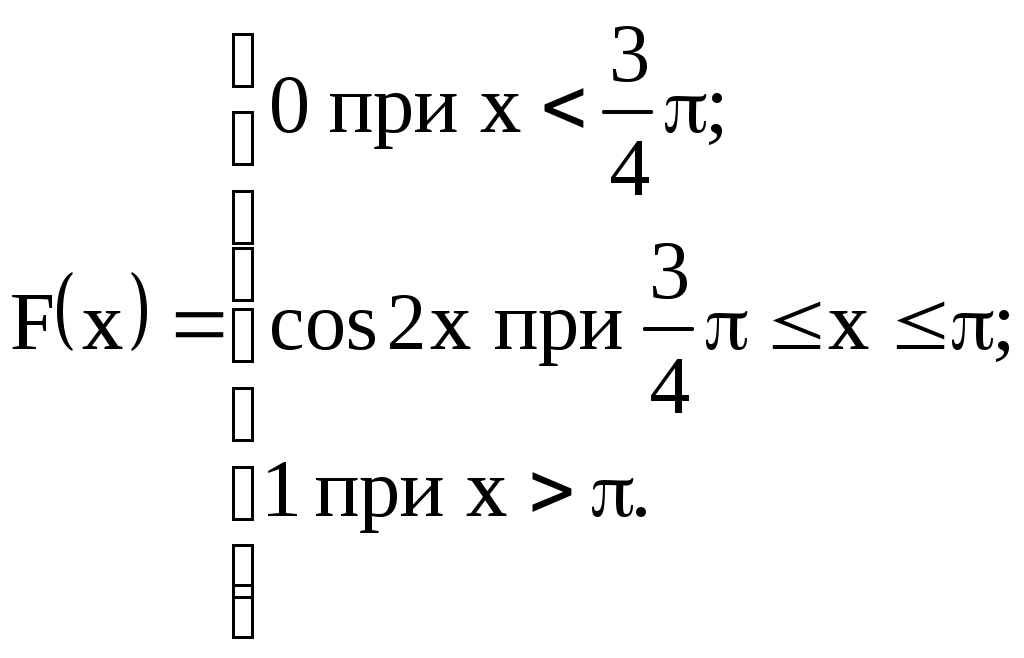 | M(X), D(X), построить графики f(x) и F(x) |
| 17) 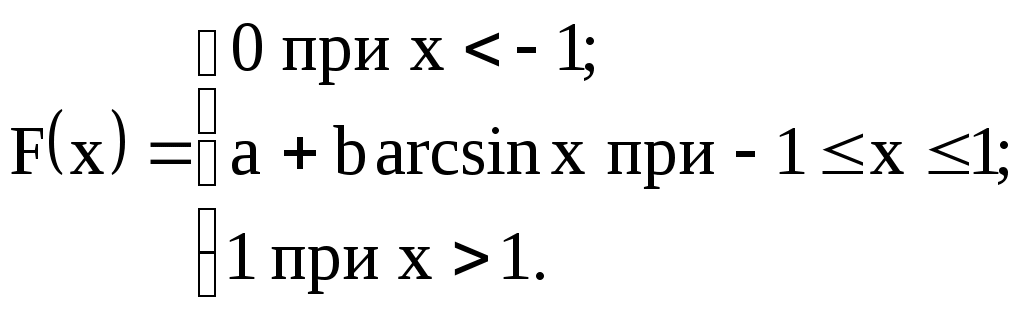 | значения "а" и "b", M(X), D(X) |
| 18) 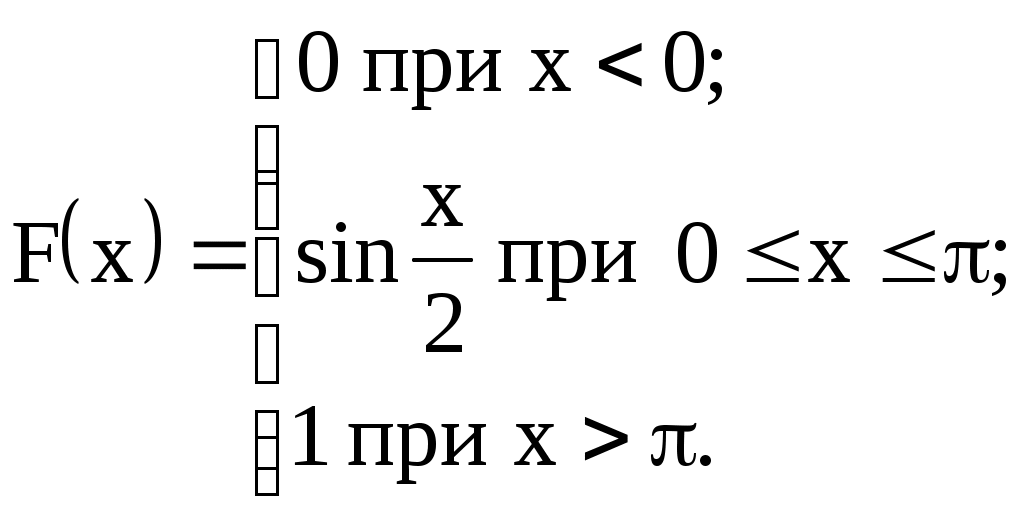 | M(X), D(X), |
| 19) 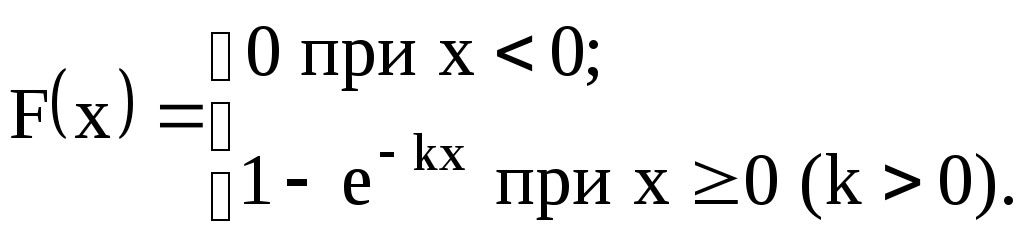 | M(X), D(X), |
| Дана функция плотности распределения вероятностей случайной величины Х | Найти |
| 20) 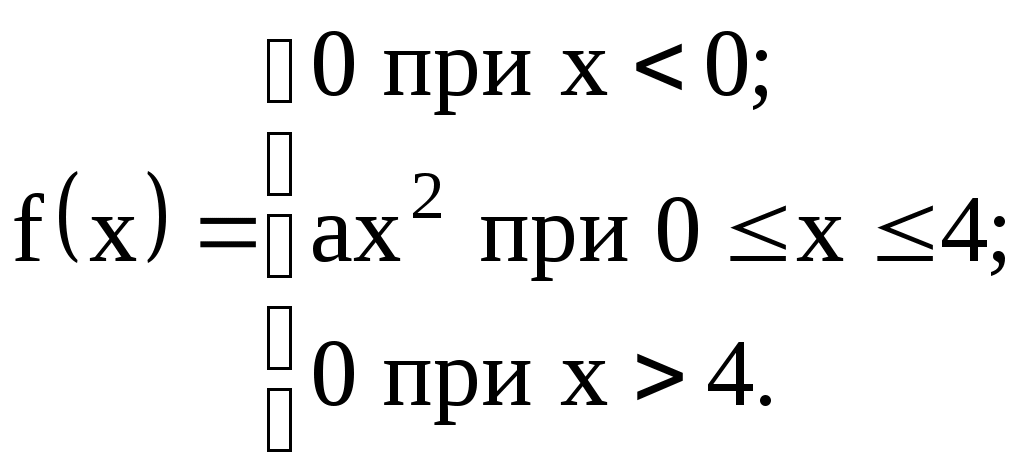 | коэффициент "а", F(x), |
| 21) | коэффициент "а", |
| Дана функция плотности распределения вероятностей случайной величины Х | Найти |
| 22) 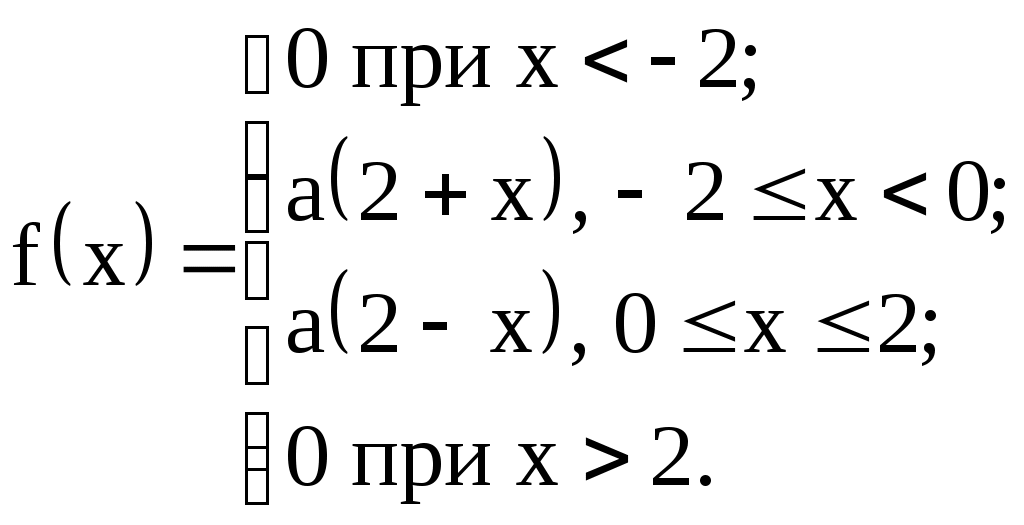 | коэффициент "а", F(x), M(X), D(X), построить графики f(x) и F(x) |
| 23) | M(X), D(X), |
24) Плотность распределения случайной величины Х задана графиком:
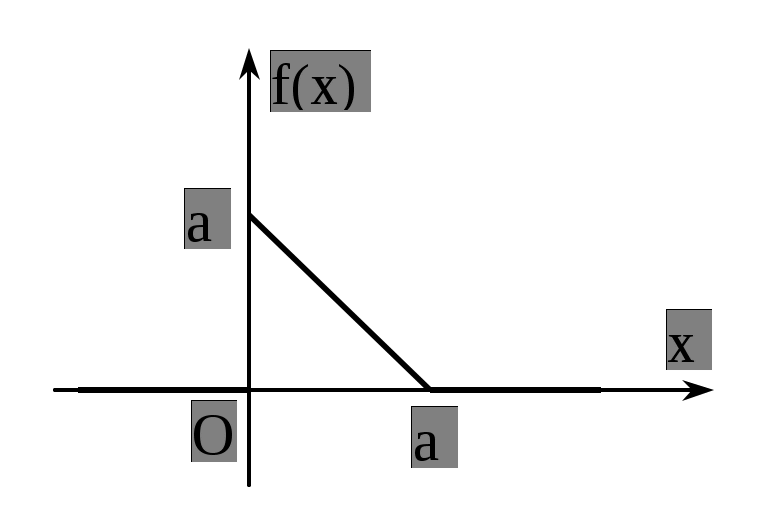
Найти f(x), F(x) , M(X), D(X).
25) Плотность распределения случайной величины Х задана графиком:
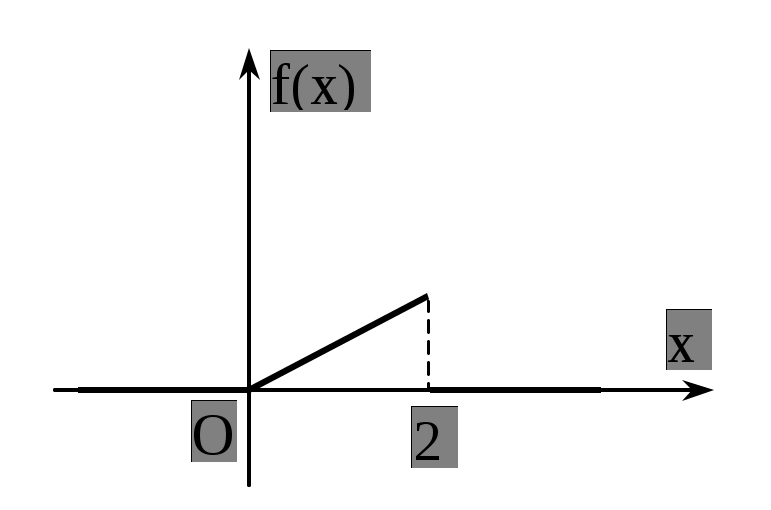
Найти f(x), F(x) , M(X), D(X).
26) Дана функция плотности случайной величины Х:
27) Плотность распределения задана функцией:
28) Функция распределения случайной величины Х имеет вид:
Найти коэффициенты А и В,
2
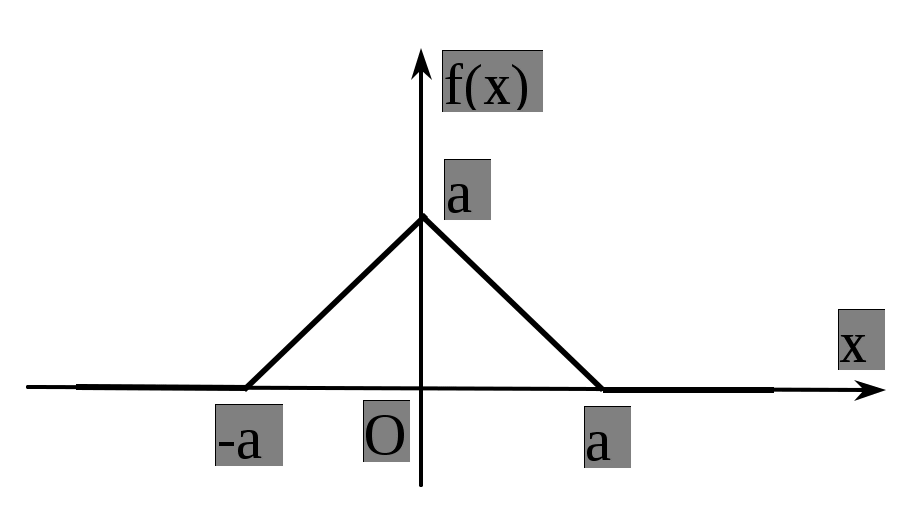
9) Плотность распределения вероятностей случайной величины Х задана графиком:
Найти f(x), F(x) , M(X), D(X).
30) Плотность распределения F(x) случайной величины Х задана графиком:
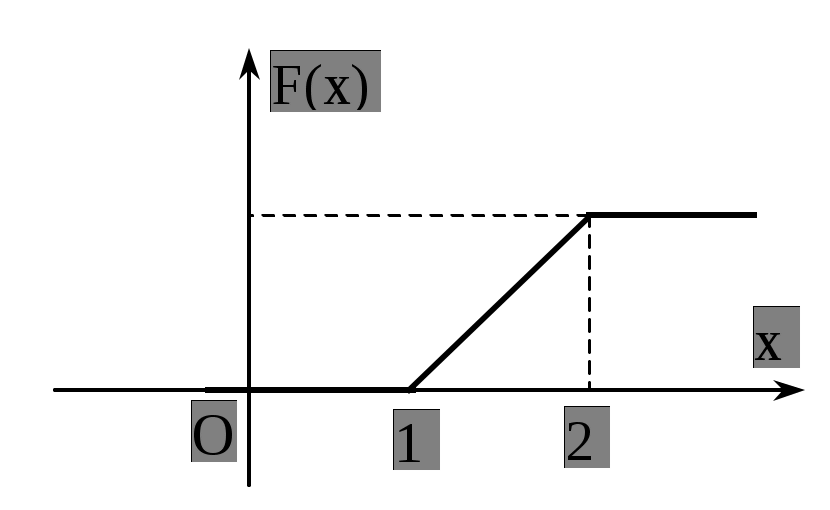
Найти f(x), F(x) , M(X), D(X),
Задание №6. Элементы статистики
Найти а) выборочную среднюю; б) выборочную дисперсию; в) выборочное среднее квадратическое отклонение по данному статистическому распределению выборки
| 1) | хi | 105 | 110 | 115 | 120 | 125 | 130 | 135 |
| | ni | 4 | 6 | 10 | 40 | 20 | 12 | 8 |