ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 100
Скачиваний: 1
Идемпотентность a ∨ a = a, a&a = aКоммутативность a ∨ b = b ∨ a, a&b = b&aАссоциативность a ∨ (b ∨ c) = (a ∨ b) ∨ c, a&(b&c) = (a&b)&c;Дистрибутивность v относительно & a ∨ (b&c) = (a ∨ b)&(a ∨ c);Дистрибутивность & относительно v a&(b ∨ c) = (a&b) ∨ (a&c);Правило двоиного отрицания не не а=аСвоиство констант a) a&1 = a, á) a&0 = 0, â) a ∨ 1 = 1, ã) a ∨ 0 = a, ä) ¯0 = 1, å) ¯1 = 0Правило де Моргана à) a&b = ¯a ∨ ¯b, á) a ∨ b = ¯a&¯b;Закон противоречия a&¯a = 0;Закон исключительного третьего a ∨ a¯ = 1.Любая логическая функция (кроме 0) имеет единственную СДНФЛюбая логическая функция (кроме 1) имеет единственную СКНФПоглощение a ∨ a&b = a a&(a ∨ b) = a;Склеивание / расщепление a&b ∨ a&¯b = a;a ∨ a¯&b = a ∨ bx → y = ¯x ∨ y, x ∼ y = xy ∨ ¯x¯y,x ⊕ y = ¯xy ∨ xy ¯x|y =¯( xy) = ¯x ∨ ¯y, x↓ y =¯( x ∨ y) = ¯x¯y.Алгебра Жегалкинаx ⊕ y = y ⊕ x, 2) x(y ⊕ z) = xy ⊕ xz, 3) x ⊕ x = 0, 4) x ⊕ 0 = xПолином Жегалкина называется нелинейным (линейным), если он (не) содержит произведения различных переменных(теорема Поста). Система F булевых функций тогда и только тогда является полной, когда для каждого из классов P0, P1, S, M, L в системе F найдется функция, не принадлежащая этому классуГраф G — пара (V, E), где V = {v1, v2, ...vn} — множество вершин, а E = {(u, v)|u ∈ V, v ∈ V } — множество ребер графа. Если множество ребер состоит из неупорядоченных пар (т.е. (u, v) = (v, u)), то граф называется неориентированным, а если пары (u, v) упорядоченные (т.е., в общем случае, (u, v) 6= (v, u)), то граф называется ориентированным или орграфом. 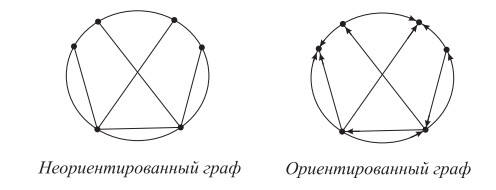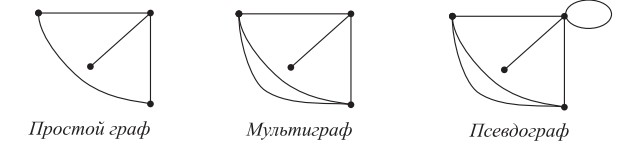В таком графе ребра принято называть дугами, а граф обозначать −→ GПростой граф — граф, множество ребер которого не содержит петель и кратных ребер. Мультиграф — граф, множество ребер которого содержит кратные ребра, но не содержит петель. Псевдограф —граф, множество ребер которого содержит петли и кратные ребраВершины u и v называются смежными, если они соединены ребром, т.е. существует (u, v) ∈ E. При этом говорят, что вершина u (или v) и ребро (u, v) инцидентны. Если граф ориентированный, то вершину u называют началом (исходом), а v — концом (заходом) дуги (u, v).Инцидентные ребра — ребра, инцидентные одной и той же вершинеСтепень вершины — число инцидентных ей ребер. Для обозначения степени вершины v используется запись deg(v). В орграфе различают также полустепень исхода deg+(v) и полустепень захода deg−(v), которые равны числу исходящих и заходящих в вершину v ребер, соответственно. Висячая вершина — вершина, степень которой равна 1.
Изолированная вершина — вершина, степень которой равна 0.Теорема "о рукопожатиях". Сумма степеней вершин графа G(V, E) равна удвоенному числу ребер, т.еСледствие. В любом графе число вершин нечетной степени четноИзоморфные графы — графы, между множествами вершин которых существует взаимно - однозначное соответствие сохраняющее отношение инцидентности (для орграфов сохраняющее также начало и конец каждой дуги).Нагруженный граф (орграф) — граф (орграф) на множестве ребер которого задана неотрицательная функция w : E(G) → R. Функция w называется весовой функцией. Замечание. Нагруженный граф также называют взвешенным. Регулярный граф степени d — простой граф, все вершины которого имеют степень d.Пустой граф порядка n — граф, состоящий из n изолированных вершин: On(V, E), V = {v1, v2, ..., vn}, E = ∅.Простой цикл длины n — простой граф, состоящий из n вершин степени 2: Cn(V, E), V ={v1, v2, ..., vn}, E ={(v1, v2),(v2, v3), ...,(vn−1, vn),(vn, v1)}. Паросочетание — простой граф, состоящий из 2n висячих вершин: nK2(V, E), V = {v1, v2, ..., vn, u1, u2, ..., un}, E = {(vi , ui)|1 ≤ i ≤ n}.Полный граф порядка n — простой граф, состоящий из n вершин степени n − 1: Kn(V, E), V = {v1, v2, ..., vn}, E = {(vi , vi)| vi ∈ V, vj ∈ V }Матрица смежности неориентированного графа G(V, E) — квадратная матрица A(G) порядка n (n = |V |), элементы которой определяются следующим образом: aij равен числу ребер, соединяющих вершины vi и vj (при этом петли считаем дважды). Матрица смежности ориентированного графа −→ G(V, −→ E ), — квадратная матрица A( −→ G) порядка n (n = |V |), элементы которой определяются следующим образом: aij равен числу дуг, ведущих из вершины vi в вершину vj (т.е. исходящих из vi и заходящих в vjМатрица инцидентности неориентированного графа G(V, E), — матрица B(G) порядка n×m (n = |V |, m = |E|), элементы которой определяются следующим образом: bij = 1, если vi и ej инцидентны; bij = 0, если vi и ej не инцидентны. Матрица инцидентности ориентированного графа −→ G(V, −→ E ), — матрица B( −→ G) порядка n × m (n = |V |, m = |E|), элементы которой определяются следующим образом: bij = 1, если vi — начало дуги ej , bij = −1, если vi — конец дуги ej ; bij = 0, если vi и ej не инцидентны.Матрица весов W(G) нагруженного графа — квадратная матрица, в которой элемент wij равен весу ребра (vi , vj ). Если вершины vi и vj не смежны, то wij = ∞. Значение элемента wii выбирается в зависимости от приложений (как правило 0 или ∞).
Матрица весов W( −→ G) нагруженного орграфа — квадратная матрица, в которой элемент wij равен весу дуги (vi , vj ). Если вершины vi и vj не смежны, то wij = ∞. Значение элемента wii выбирается в зависимости от приложенийПодграф графа — граф, все вершины и рёбра которого содержаться среди вершин и рёбер исходного графаОперации на графах1. Удаление ребра. При удалении ребра из графа G получаем новый граф G0, который является подграфом исходного. Множество вершин графа G0 совпадает с множеством вершин графа G, а ребер на одно (удаленное) меньше.2. Удаление вершины. Удаление вершины v из графа G производится вместе с удалением всех инцидентных ей ребер. В результате, получаем новый граф G0 , который является подграфом исходного. Вершин у графа G0 на одну (удаленную) меньше, чем у графа G, а ребер меньше на deg v.3. Добавление вершины. При добавлении вершины в граф G получаем новый граф G0, для которого исходный граф G является подграфом.Множество ребер графа G0 такое же как у графа G, а вершин на одну (добавленную) больше. Добавленная вершина является изолированной.4. Добавление ребра. При добавлении ребра в граф G получаем новый граф G0 , для которого исходный граф G является подграфом. Множество вершин графа G0 такое же как у графа G, а ребер на одно (добавленное) больше.5. Отождествление вершин. При отождествлении вершин u и v графа G получаем новый граф G0 следующим образом: удалим вершины u и v; добавим новую вершину w; добавим ребра (w, vi), где vi ∈ Γ(u) ∪ Γ(v) (т.е. ребра, соединяющие новую вершину со всеми вершинами, которые были смежными с удаленными вершинами).6. Стягивание ребра. При стягивании ребра e графа G получаем новый граф G0, у которого отождествлены вершины, инцидентные данному ребру, а само ребро исключено из множества ребер.7. Размножение вершины. При размножении вершины u графа G получаем новый граф G0 следующим образом: добавим новую вершину u’; добавим новое ребро (u, u’); добавим ребра (u’, vi), vi ∈ Γ(u) (т.е. ребра, соединяющие новую вершину со всеми вершинами из окрестности вершины u).8. Расщепление вершины. При расщеплении вершины u графа G получаем новый граф G0 следующим образом: разобьем окрестность вершины u на два произвольных непересекающихся подмножества Γ1 и Γ2; удалим вершину u из графа; добавим новые вершины u1 и u2; добавим ребра (u1, vi), vi ∈ Γ1, (u2, wj ), wj ∈ Γ2 и (u1, u2) (т.е. ребра, соединяющие новые вершины со всеми вершинами
, которые были смежными с удаленной вершиной и ребро, соединяющее новые вершины между собой).
9. Дублирование вершины. При дублировании вершины u графа G получаем новый граф G0 следующим образом: добавим вершину u’; добавим ребра (u’, vi), vi ∈ Γ(u) (т.е. ребра, соединяющие новую вершину со всеми вершинами, которые смежны с вершиной u).
10. Разбиение ребра. При разбиении ребра (u, v) графа G получаем новый граф G0 следующим образом: удалим ребро (u, v) из множества рёбер графа; добавим новую вершину w; добавим рёбра (u, w) и(w, v).
11. Объединение графов. При объединении графов получаем граф, состоящий из всех вершин и ребер исходных графов: G1(V1, E1) ∪ G2(V2, E2) = G(V1 ∪ V2, E1 ∪ E2)
12. Пересечение графов. При пересечении графов получаем граф, множества вершин и рёбер которого состоят из вершин и рёбер, принадлежащих исходным графам:G1(V1, E1) ∩ G2(V2, E2) = G(V1 ∩ V2, E1 ∩ E2).
13. Соединение графов. При соединении графов получаем граф, который является результатом их объединения и добавления ребер, инцидентных вершинам из разных графов: G1(V1, E1)+G2(V2, E2) = G(V1∪V2, E1∪E2∪{(v1, v2)| v1 ∈ V1, v2 ∈ V2}) (при условии, что V1 ∩ V2 = ∅, E1 ∩ E2 = ∅).
14. Декартово произведение графов. Множество вершин произведения G1×G2 графов G1(V1, E1) и G2(V2, E2) состоит из упорядоченных пар (u1, u2), u1 ∈ G1, u2 ∈ G2: V (G1 × G2) = V (G1) × V (G2).
Маршрут в неориентированном графе — последовательность из вершин и ребер vi0, ei1, vi1, ei2, ...eik, vik, где любые два соседних элемента инцидентны. Если vi0 = vik , то маршрут называется замкнутым,иначе — открытым.
Цепь — маршрут, все ребра которого различны. Замкнутая цепь называется циклом.
Простая цепь — маршрут, все вершины которого различны. Замкнутая простая цепь называется простым циклом
Длина маршрута равна количеству ребер в нем (с повторениями).
Расстояние d(u, v) от вершины u до вершины v равно количеству ребер в кратчайшей простой цепи (пути) из u в v.
Вершина u достижима из вершины v, если существует цепь (путь) из v в u.
Связный неориентированный граф — граф, для любых двух вершин которого существует соединяющий их маршрут.
Компонента связности неориентированного графа — максимальный по включению связный подграф.
Точка сочленения — вершина, удаление которой увеличивает число компонент связности.
Мост — ребро, удаление которого увеличивает число компонент связности.