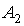ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Если любые две вершины орграфа−→G достижимы друг из друга, то орграф сильно связный. Если для любых u, v ∈ V ( −→ G) u достижима из v или v достижима из u, то орграф связный. Если связным является граф G, полученный из−→ G заменой всех дуг на ребра (отменой ориентации), то −→G — слабо связный
Матрица достижимости R( −→ G) орграфа −→ G — матрица порядка n, у которой rij = 1 , если вершина vj достижима из вершины vi и rij = 0 — в противном случае.
Матрица сильной связности орграфа −→G — матрица S( −→ G) порядка n, у которой sij = 1 , если вершина vj достижима из вершины vi и вершина vi достижима из вершины vj; sij = 0 — в противном случае.
Конденсат ориентированного графа — орграф, полученный из данного отождествлением вершин, входящих в одну компоненту сильной связности.
Дерево — связный граф без циклов. Несвязный граф без циклов называется лесом.
Остов или остовное дерево графа — любой его подграф, содержащий все вершины графа и являющийся дерево
Цикломатическое число λ(G) графа G — число ребер, которые необходимо удалить, чтобы граф стал ациклическим (т.е., деревом, если G связный и лесом, если G — несвязный).
Обход графа — некоторое систематическое перечисление его вершин или ребер
Эйлеров цикл (цепь) — цикл (цепь), содержащий все ребра графа ровно один раз и все вершины графа (возможно, несколько раз).
Эйлеров граф — граф, содержащий эйлеров цикл
Длина пути в нагруженном орграфе — это сумма весов дуг из которых состоит данный путь. Длина маршрута в неориентированном графе определяется аналогично
Булева функция f(x1, x2, . . . , xn) тогда и только тогда имеет простую дизъюнктивную декомпозицию в форме f(X) = = F(g(A1), A2), когда карта декомпозиции функции f для пары (A1, A2) содержит не более двух различных столбцов
Дизъюнктивная декомпозиция функции f(x1, x2, . . . , xn) вида f(x1, x2, . . . , xn) = F(g(A1), A2) называется простой.
Ориентированная бесконтурная сеть, в которой полюса делятся на входные (входы) и выходные (выходы), называется схемой из функциональных элементов
Функциональным элементом называется всякий подмультиграф схемы,состоящий из невходного полюса a, помеченного соответствующим символом f, и вершины, из которых исходят дуги в вершину a
Маршрут в неориентированном графе — последовательность из вершин и ребер vi0, ei1, vi1, ei2, ...eik, vik, где любые два соседних элемента инцидентны. Если vi0 = vik, то маршрут называется замкнутым, иначе — открытым.
Цепь — маршрут, все ребра которого различны. Замкнутая цепь называется циклом.
Простая цепь — маршрут, все вершины которого различны. Замкнутая простая цепь называется простым циклом.
Замечание. Цепь в ориентированном графе — путь, а цикл — контур.
Длина маршрута равна количеству ребер в нем (с повторениями).Расстояние d(u, v) от вершины u до вершины v равно количеству ребер в кратчайшей простой цепи (пути) из u в v.
Автоматы можно рассматривать как механизмы, состоящие из:
-
блока управления, который может пребывать в различных состояниях (S внутренний алфавит); -
входного канала; -
выходного канала.
Входной канал считывает входные сигналы (Х) из внешней среды. Выходной канал выдает выходные сигналы (Y) во внешнюю среду
Конечный .Детерминированный .Автомат . называется система
, где 
- алфавит состояний, 
– входной алфавит, 
– выходной алфавит. Множества S, X, Y – конечные.
– функция переходов,
– функция выходов.Если в автомате выделено одно состояние , называемое начальным (обычно
), то автомат называется инициальным.Две диаграммы Мура называются изоморфными, если они могут быть превращены одна в другую переобозначением вершин.
Два автомата называются изоморфными, если их диаграммы Мура изоморфны.
Состояния
и 
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова
х результат работы автомата
такой же, как и для 
.
В частном случае, когда
=