Добавлен: 06.12.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оглавление
Задача № 1 2
Задача №2 5
Задача № 1
Построить график изменения температуры в пластине на участке от х = 1 см до х = - 5см, у=1,5 смпри нагреве ее подвижным линейным источником теплоты, когда достигнуто предельное квазистационарное состояние; q=5800 Дж/с; v=0,35 см/с; δ=2см; а=0,085 см2/с; λ=0,42 дж/см·с·град; сρ=4,9 Дж/см3·град.
Температуру определяем для точек х=1; 0; - 1; - 2; - 3; - 4; -5 см.
Для удобства вычислений результаты представляем в виде таблицы:
| х, см | r, см | 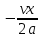 | 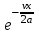 | 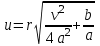 | 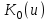 | Т, °С |
| 1 | 1,8 | - 2,6 | 0,13 | 3,74 | 0,015193 | 2 |
| 0 | 1,5 | 0 | 1 | 3,11 | 0,031086 | 34 |
| -1 | 1,8 | 2,06 | 7,84 | 3,74 | 0,015193 | 131 |
| -2 | 2,5 | 4,12 | 61,39 | 5,18 | 0,003056 | 206 |
| -3 | 3,35 | 6,18 | 480,98 | 6,95 | 0,0004507 | 238 |
| -4 | 4,27 | 8,24 | 3768,53 | 8,85 | 0,0000597 | 247 |
| -5 | 5,22 | 10,29 | 29526,7 | 10,82 | 0,0000076 | 246 |
Радиус определяется по зависимости:
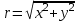 ;
;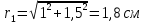
;
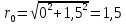 см;
см;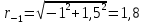 см;
см;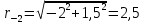 см;
см;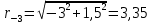 см;
см;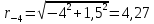 см;
см;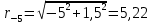 см;
см;Коэффициент температуроотдачи находим по формуле:
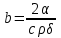 .
.Коэффициент теплоотдачи а находим по графику на рис. 16.6 [2.2] для Тср=6000 С, α
 = 6·10-3 Дж/см2·с·град.
= 6·10-3 Дж/см2·с·град.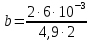 1/с.
1/с.Для определения значения функции Бесселя 1-го рода нулевого порядка можно воспользоваться справочными данными или зависимостью:
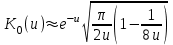 .
.Температуру определяем по формуле:
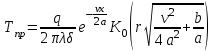 ;
;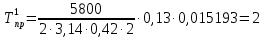 °С;
°С;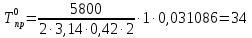 °С;
°С;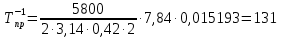 °С;
°С;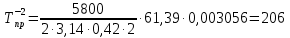 °С;
°С;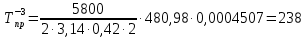 °С;
°С;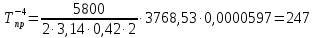 °С;
°С;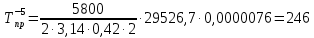 °С;
°С;По рассчитанным значениям строим график (рис.1) распределения температуры:
t
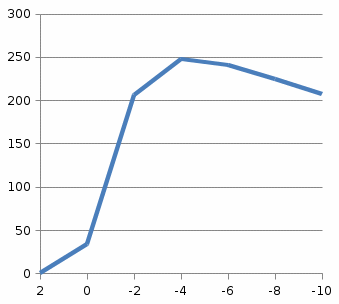
X, см рис.1.
График распределения температуры.
Задача №2
Листы из низколегированной закаленной стали δ=5 см свариваются за один проход дуговой сваркой при токе 500 а, напряжение дуги U=34 в и скорости v=0,55 см/с, η=0,85. Определить ширину зоны отпуска, которая находится примерно между изотермами 580 °С и 780 °С.
Теплоемкость стали 5,0 дж/смЗ·град.
Находим эффективную мощность источника теплоты по формуле:
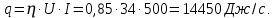
Воспользуемся формулой для мощных 6ыстродвижущихся источников и определим ширину зоны, нагревавшейся до Т=580 °С:
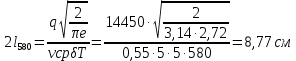
Аналогично определим ширину зоны, нагревшейся до Т=780 °С:
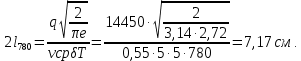
Тогда ширина зоны отпуска определится: