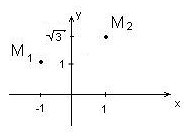
Типовая задача. Даны числа и . а) Изобразить числа и на комплексной плоскости; б) Найти , , , ;в) Найти модуль и аргумент чисел и . г) Представить числа в тригонометрической и показательной форме, найти , , ,.Решение. ►а) Изобразим числа на комплексной плоскости. При этом числу будет соответствовать точка , числу - точка .б) ; ;

---

.Получим: , , , .г) Чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической и показательной применим формулы: и .Используя, ранее полученные результаты, получим: формула МуавраДифференцирование функций.Формулы дифференцирования

1.	10.
2.	11.
3.	12.
4.	13.
5.	14.
6.	15.
7.	16.
8.	17.
9.	18.
	19.

---

Правила дифференцирования

1.	4.
2.	5.
3.	6.

Пример. Найти производную функции .Решение. Данная функция является сложной, порядок следования промежуточных функций таков: , . Согласно правилу дифференцирования сложной функции, находим .Ответ: 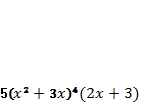.Задание 2

1. 
   Найти производные указанных функций:
   

.1. а) ; б) ; в) ..2. а) ; б) ; в) ..3. а) ; б) ; в) ..4. а) ; б)

---

; в) .

.5. а) ; б) ; в) .

.6. а) ; б) ; в) .

.7. а) ; б) ; в) .

.8. а) ; б) ; в) .

.9. а) ; б) ; в) .

.10. а) ; б) ; в) .

.11. а) ; б) ; в) .

.12. а) ; б) ; в) .

.13. а) ; б)

---

; в) .

.14. а) ; б) ; в) .

.15. а) ; б) ; в) .

.16. а) ; б) ; в) .

.17. а) ; б) ; в) .

.18. а) ; б) ; в) .

.19. а) ; б) ; в) .

.20. а) ; б) ; в) .
Типовая задача. Найти производные указанных функций:

а) ; б) ; в) .

Решение.

►а)

---

Смотрите также файлы

• Доверенность на получение трудовой книжки.doc

• Комплект оценочных средств к зачету по дисциплине Основы алгоритмизации и программирования.docx

• Цель сформировать умения планировать, проектировать и моделировать различные формы логопедической работы на основе знания основных принципов их организации и проведения. 34.docx

• План мероприятий для устранение 1 Прочитать 3 книги по тайм менеджменту 2 Внедрить правила из книг в работу.docx

• Решение дифференциального уравнения. Найти решение задачи Коши.docx