Файл: Методические указания и контрольные задания по выполнению контрольной работы для заочного отделения по учебной дисциплине.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 42

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Перепишем данную функцию, введя дробные и отрицательные показатели: .

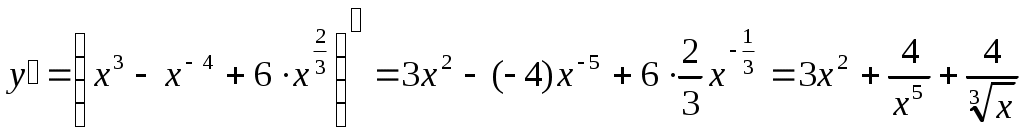Применяя правило дифференцирования алгебраической суммы и формулу дифференцирования степенной функции , имеем:

.

б)

Применяя правило производной произведения двух функций и формулы , , имеем:



в)

Применяем правило дифференцирования частного двух функций :




Интегрирование функций
- совокупность первообразных, ,
Таблица основных интегралов

1.

11.

2.

12.

3.

13.

4.

14.

5.

15.

6.

16. ,

7.

17. ,

8.

18. ,

9.

19. ,

10.




1

2.

3.
Методы интегрирования

1. Непосредственное интегрирование

2. Метод интегрирования подстановкой (заменой переменной)



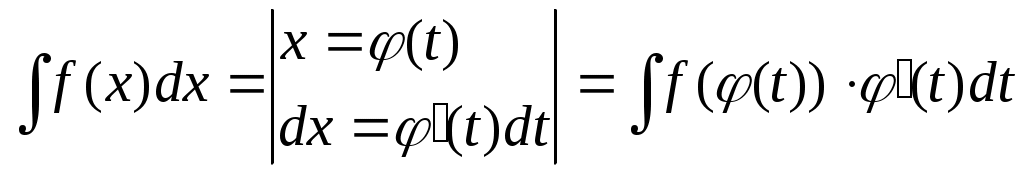
3. Метод интегрирование по частям:

- формула Ньютона Лейбница
Вычисление площади плоской фигуры




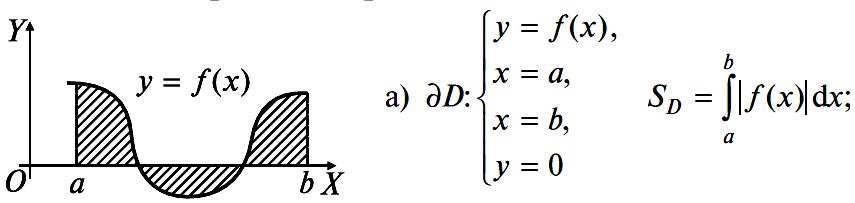
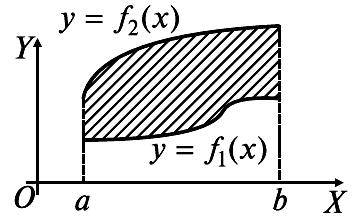
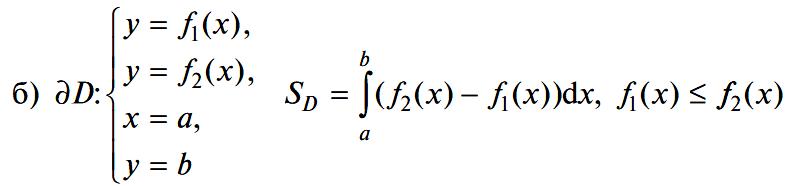
Физические приложения определенного интеграла

Величины
А – работа;

F – сила;

N - мощность.
m –масса тонкого стержня

p – линейная плотность
Q –электрический заряд;

I – сила тока.
S –перемещение;

v –скорость.
Q –количество теплоты;

с – теплоёмкость.

Вычисление интеграла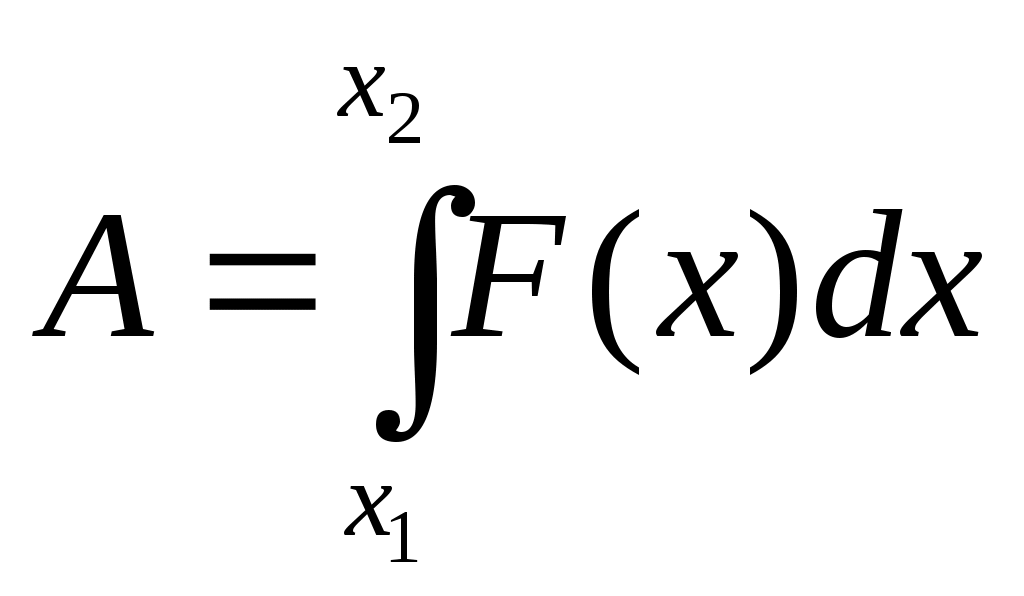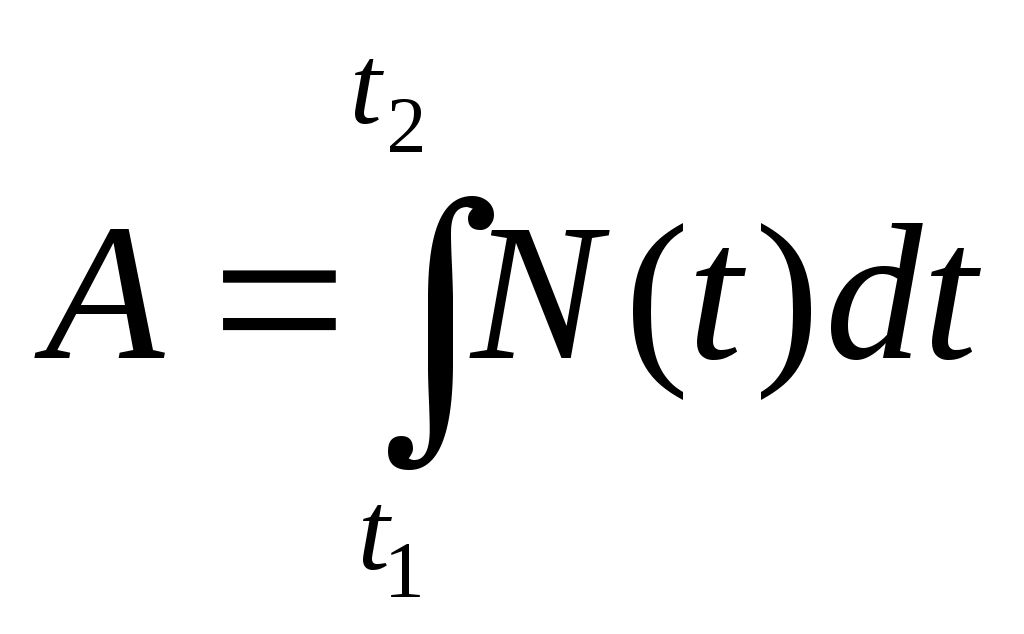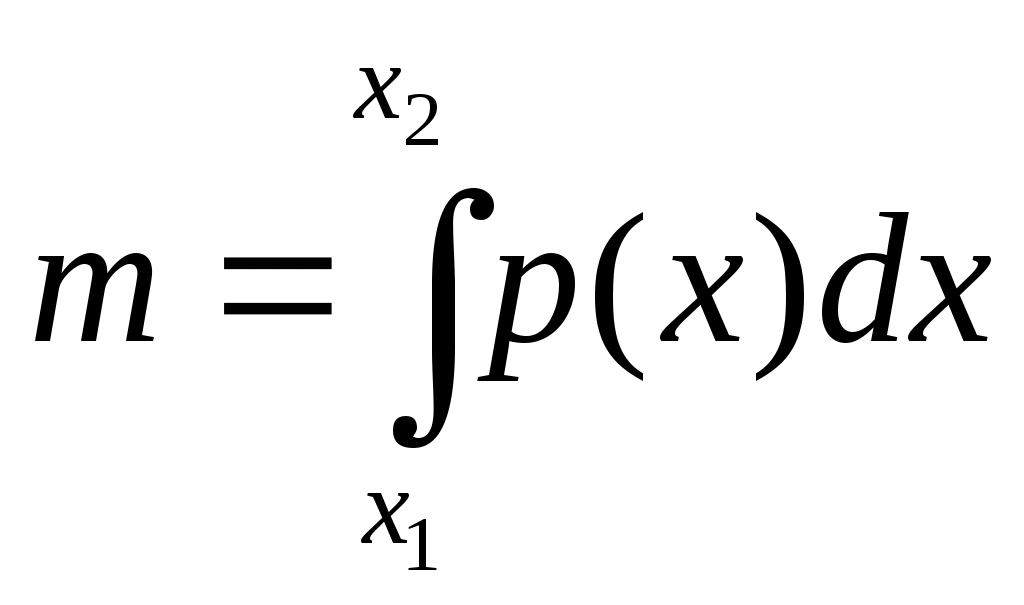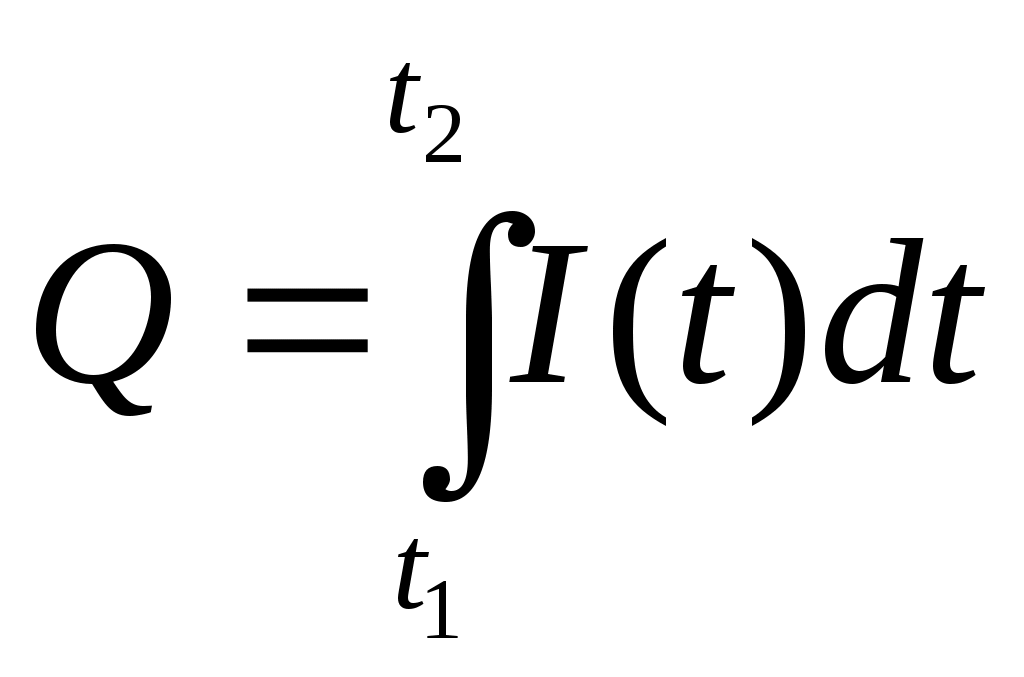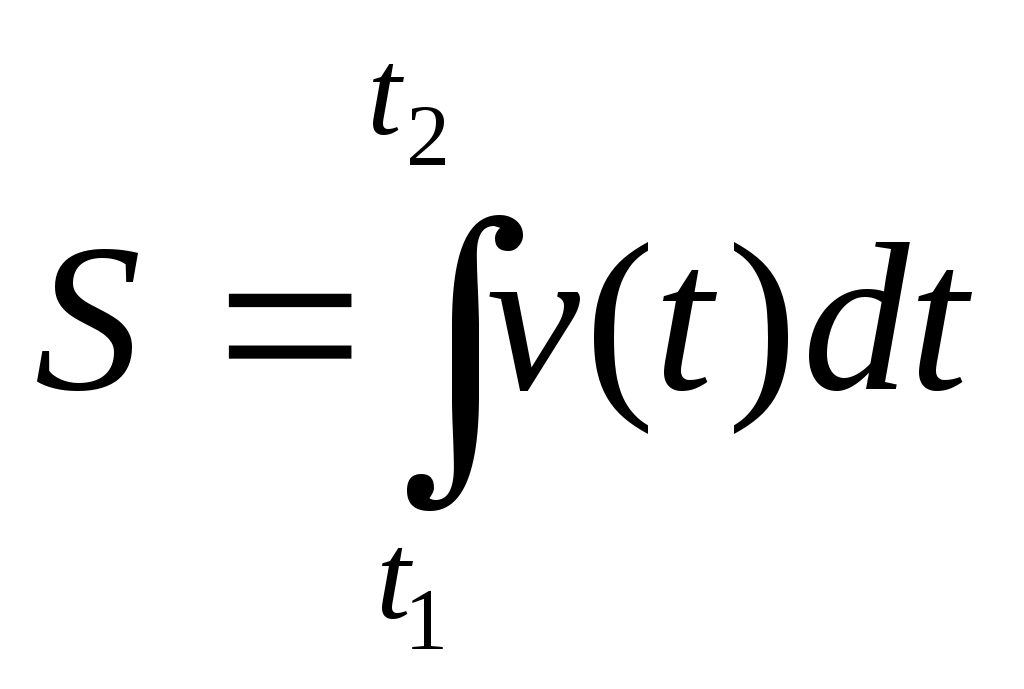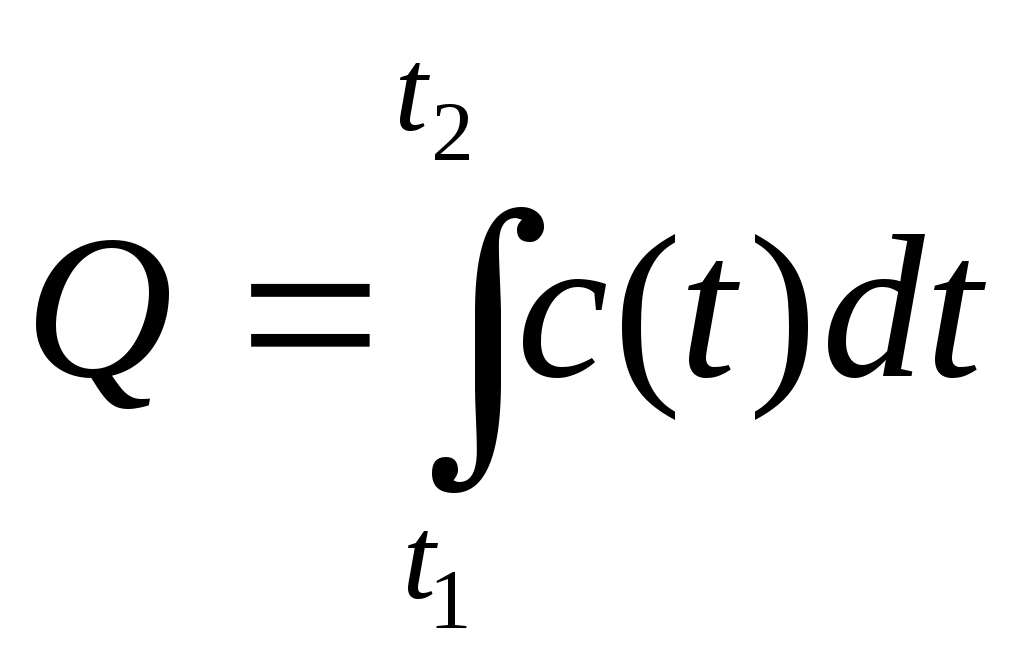
;








Задание 3
1. Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.

.1. а) ; б) ;

.2. а) ; б) ;

.3. а) ; б) ;

.4. а) ; б) ; .

.5. а) ; б) ;

.6. а) ; б) ; .
.7. а) ; б) ; .

.8. а) ; б) ; .

.9. а) ; б) ;

.10. а) ; б) ;.

.11. а) ; б) ;

.12. а) ; б) ;

.13. а)
; б) ; .

.14. а) ; б) ;.

.15. а) ; б) ;.

.16. а) ; б) ;.

.17. а) ; б) ;

.18. а) ; б) ;.

.19. а) ; б) ;.

Задача Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием:

а) ; б) ;.

Решение.

► а) .

Предварительно преобразуем подынтегральную функцию, затем применив свойства неопределенного интеграла и табличный интеграл, получим:

,



.

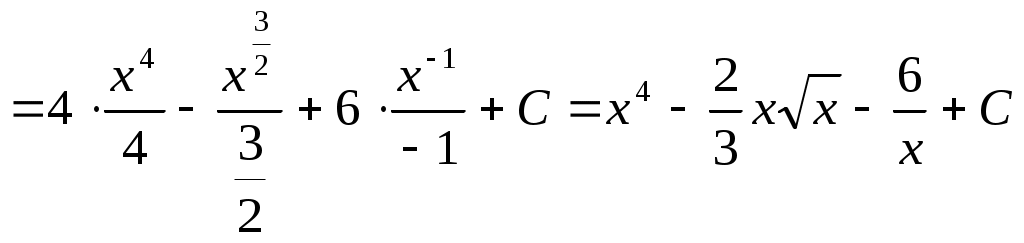Сделаем проверку:



.








Задание 4

Смотрите также файлы