Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.

.1.		2.15.	,
.2.		2.16.
.3.		2.17.
.4.		2.18	, ,
.5.		2.19.
.6.		2.20.
.7.		2.21.
.8.		2.22.
.9.	,	2.23.
.10.		2.24.
.11.		2.25.
.12.		2.26
.13.	, , ,	2.27.
.14.	,	4.28.

---

Типовая задача . Вычислить площадь фигуры, ограниченной параболой и прямой .

Решение.

►Площадь фигуры, ограниченная сверху непрерывной кривой , снизу – непрерывной кривой , слева – прямой и справа прямой , вычисляется по формуле

.

В тех случаях, когда заданные кривые образуют замкнутую область, и прямые и не заданы, то числа и совпадают с абсциссами точек пересечения кривых. Найдём точки пересечения заданных линий. Для этого решим совместно систему уравнений:

.

,

,

.

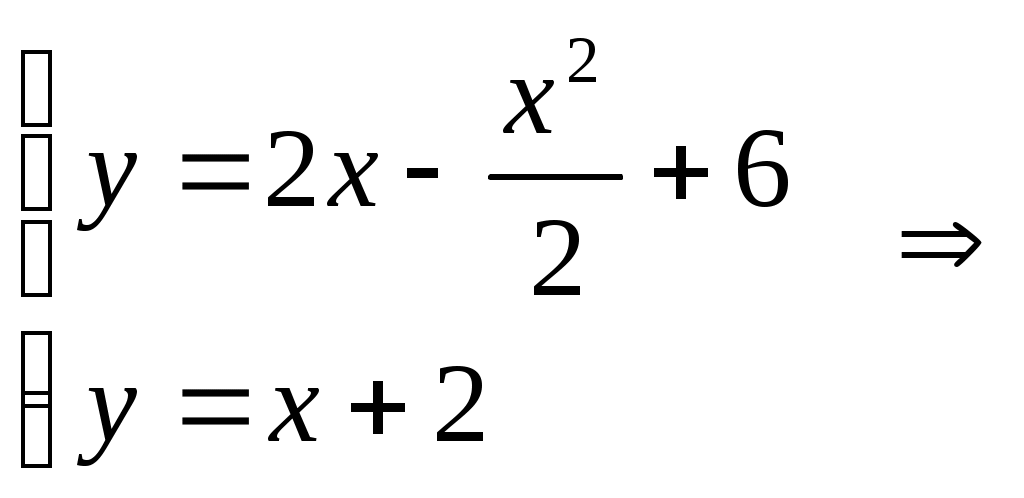
Получим и ; следовательно, и .

Парабола и прямая пересекаются в точках и

---

. Для построения прямой достаточно двух найденных точек, но для параболы этих данных недостаточно. Поэтому найдем дополнительные точки:

а) вершина параболы расположена в точке с координатами ; в данной задаче парабола ( , ) имеет вершину в точке , т.е. .

б) Так как , следовательно, ветви параболы направлены вниз, и она пересекает ось абсцисс. Найдём точки пересечения с осью Ох:

,

,

,

.



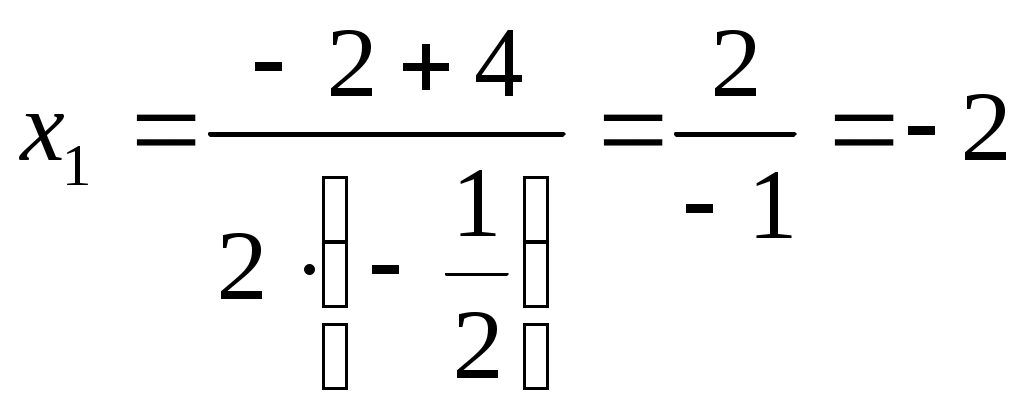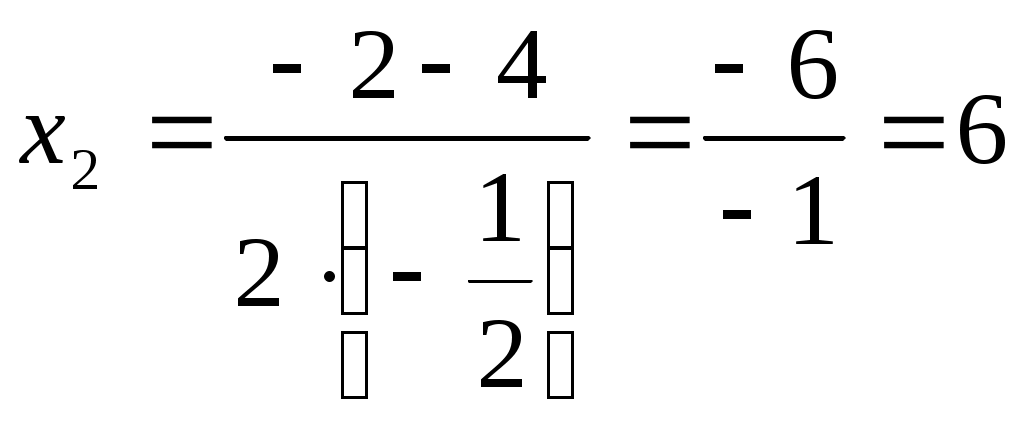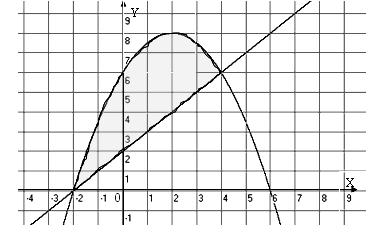
Рис. 1

Следовательно, парабола пересекает ось Ох в точках с координатами и (рис. 1).

Применяя , получим:



.

Ответ:

---

кв. ед.◄

---

Дифференциальные уравнения
Решением (частным решением) уравнения или на интервале (a,b) называется любая функция , которая, будучи подставлена в это уравнение вместе со своей производной φ′(x), обращает его в тождество относительно . Уравнение , определяющее это решение как неявную функцию, называется интегралом (частным интегралом) дифференциального уравнения. На плоскости с фиксированной декартовой прямоугольной системой координат уравнение определяет некоторую кривую, которая называется интегральной кривой дифференциального уравнения.

Функция называется общим решением уравнения или , если при любом допустимом значении параметра С она является частным решением этого уравнения и, кроме того, любое его частное решение может быть представлено в виде при некотором значении параметра C. Уравнение , определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
.

.

Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде

---

Смотрите также файлы

• Доверенность на получение трудовой книжки.doc

• Комплект оценочных средств к зачету по дисциплине Основы алгоритмизации и программирования.docx

• Цель сформировать умения планировать, проектировать и моделировать различные формы логопедической работы на основе знания основных принципов их организации и проведения. 34.docx

• План мероприятий для устранение 1 Прочитать 3 книги по тайм менеджменту 2 Внедрить правила из книг в работу.docx

• Решение дифференциального уравнения. Найти решение задачи Коши.docx