Файл: Уроковконсультаций в 11 классе. Задачи с параметром.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 16

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

КОУ ВО «ЦЛПДО»

Разработка уроков-консультаций в 11 классе.

«Задачи с параметром».

Подготовила Л.И. Гоптарь.

-Воронеж-

2020г.

Цели:

  1. Знать, что такое уравнение с параметрами, что значит решить такое уравнение.

  2. Уметь решать простейшие уравнения с параметрами.

  3. Развивать интерес к заданиям исследовательского характера.

Ход урока.

1.Организационный момент.

2.Устные упражнения.

1) Определите тип уравнения. Сколько корней у него может быть? Решите его.

а) 2х – 6 = 0, 0х = 6, 0х = 0.

Повторим основные сведения:

ах = в - линейное

а 0 х = - один корень,

а = о, в 0 - нет корней,

а = 0, в = 0 - х – любое число.

б) Определите количество корней 2х2 – 3х + 8 = 0 (т.к. Д < 0, то нет корней.)

Измените условие так, чтобы полученное уравнение имело два корня.

Повторим основные сведения:

ах2 + вх + с = 0 , а 0 - квадратное

1. Если Д> 0, то 2 корня,

2. Если Д = 0, то 1 корень,

3. Если Д< 0, то нет корней.

в) = 5

Измените условие так, чтобы полученное уравнение не имело корней.

г) lхl = 10

Измените условие так, чтобы полученное уравнение не имело корней.

2) Чем отличаются уравнения ах = 6 и 3х = 6, ах2 + 7х + с = 0 и 2х2–3х+6 = 0?

(Ответ учащихся: в первом и третьем уравнениях не числовые коэффициенты).

Учитель:

Действительно, в уравнениях ах = 6 и ах2 + 7х + с = 0 не числовые коэффициенты, а буквенные. Именно такие уравнения и станут предметом нашего изучения на уроке.

3. Изучение нового материала.

1) Определение. Уравнение, в котором помимо переменной содержится буквенное выражение, называется уравнением с параметрами.


Примеры: аx + в = 0 (x – переменная, а и в – параметры),

аx2 + вx + с = 0 (x – переменная, а, в и с – параметры).

2) Чаще всего встречаются две постановки задач.

Первая: для каждого значения параметра найти все решения заданного уравнения.

Вторая: найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.

Определение. Решить уравнение с параметром – значит, для любого допустимого значения параметра найти множество всех корней заданного уравнения.

Решение уравнений. (Учащиеся привлекаются к поиску ответов).

1). Простые уравнения без ветвлений:

а) x – а = 0 Ответ: приа ( - , + ) х = а.

б) 5x = а Ответ: при а ( - , + ) х = .

в) x : 8 = а Ответ: при а (- , + ) х = 8а.

2). Простые уравнения с ветвлениями:

а) аx = 10 Ответ: при а 0 х = , при а = 0 решений нет.

б) 0x = а Ответ: при а 0 корней нет, при а = 0, х – любое число.

в) [х] = а Ответ: приа< 0 корней нет, при а = 0 х = 0, при а
> 0, х = а.

г) (а2 – 4)x = а2 + а – 6

Решение г). Если а2 – 4 0, т.е. а ± 2, то х = .

Приа = -2 уравнение имеет вид: 0х = -4, т.е. не имеет корней.

Приа = 2 исходное уравнение принимает вид: 0х = 0, т.е. х – любое число.

Ответ: приа ± 2  х = ,

приа = - 2 корней нет,

приа = 2 х – любое число.

4. Закрепление. (Коллективный поиск решения, оформление решения в тетрадях учащихся).

1) Решить уравнение а (а – 1) = а – 1.

Решение. Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а. Будем решать его «как обычно»: делим обе части уравнения на коэффициент при неизвестном. Но всегда ли возможно деление?(Нет.Делить на ноль нельзя.)

Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен 0. Получим:

  1. а = 1, тогда уравнение примет вид 0·х = 0, где х – любое число;

  2. а = 0, тогда 0∙х = - 1 – уравнение корней не имеет;

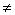  3. а 0, а 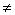1, тогда а (а – 1)·х = а – 1 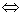х = .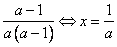

Ответ: 1) если а 0, а 1, то х =
;

2) если а = 1, то х – любое число;

3) если а = 0, то корней нет.

2) Решить уравнение (а – 1)х2 + 2 (2а – 1)х + 4 а + 3 = 0.

Решение. Рассмотрим два случая:

  1. а = 1 – получим линейное уравнение 2х + 7 = 0, откуда х = - 3,5;

  2. а 1 – получим квадратное уравнение.

Рассмотрим дискриминант: D = (2а – 1)2 – (а – 1)(4а + 3) = - 3а + 4.

Далее, если а > , то D < 0 и уравнение корней не имеет.

Если же а , то х1,2 = .

Ответ: 1) если а > , то корней нет;

2) если а = 1, то х = - 3,5;

3) если а и а 1, то х1,2 = .

3)При каких значениях а уравнение sin 2x – asinx=0 имеет решения для каждого а, указать их?

Решение.

2sin x cos x – a sin x = 0;

sin x (2 cos x-a) = 0

Sin x = 0 или 2cos x – a = 0

  1. x=πn при любом значении а




  1. cosx = a/2, есть решения, если |а|/2≤1, -2≤а≤2

x = ± arccosa/2 + 2πm, m € Z

Итак, при а € (-∞;+ ∞), х = πn, n € Z

при а € [-2;2], х = ± arcosa/2 + 2πm, m € Z

Ответ: а € (-∞;+ ∞), х = πn, n € Z

а € [-2;2], х = ± arcos a/2 + 2πm, m € Z

5.Примеры заданий на исследование уравнений.

Особенно часто встречаются задачи на расположение корней квадратного уравнения. При их решении хорошо «работают» графические иллюстрации. Расположение корней относительно заданных точек плоскостью определяется направлением ветвей соответствующей параболы, координатами вершины, а также значениями в заданных точках.

Например.

1) При каких значениях параметра а уравнение (а2 + а + 1)х2 + (2а – 3)х + а – 5 = 0 имеет два корня, один из которых больше 1, а другой меньше 1?

Решение. Пусть f(х) = (а2 + а + 1)х2 + (2а – 3)х + а – 5. Так как а2 + а + 1 >0, то для квадратичной функции f(х) условие задачи может выполняться только при условии f (1) <0.



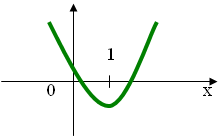
Решая неравенство f(1) = а2 + 4а – 7 < 0, получим, что -2 - < а < - 2 + .

Ответ: -2 - < а < - 2 + .

2) При каких значениях параметра m корни уравнения (m – 1)х2 – 2mх + m + 3 = 0 положительны?

Решение. Пусть f(х) = (m-1)х2 - 2 mх + m + 3 тогда:

1) если, m = 1,то -2х + 4=0, х= 2- корень положителен;

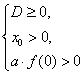
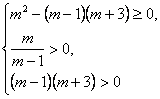
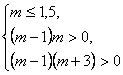
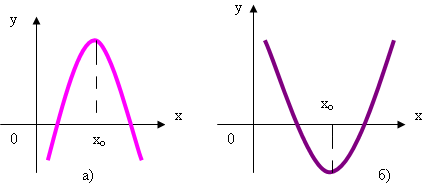
2) если m 1, то с помощью рисунка можно получить следующие соотношения:




Рассмотрим 2 случая:

1) если m-1< 0( рис. а)), тогда из 2 и 3 неравенств последней системы получим m + 3 < 0, т.е. окончательно m < -3.

2) если m -1> 0,( рис. б)), тогда из 2 и 3 неравенств последней системы получим, что m > 1, т.е. окончательно 1,5

Смотрите также файлы