res = -max(negative) + 1

else:

res = -max(nextCodes)

results[(x,y)] = res # (3)

return res

9. 
   добавленные строчки выделены голубым фоном; в строке (1) создаётся пустой словарь (глобальная переменная), ключом в этом словаре будет кортеж, описывающий позицию (x, y);
   
10. 
    в строке (2) мы проверяем, нет ли в словаре кода для запрошенной позиции; если есть, то сразу возвращаем этот код
    
11. 
    в строке (3) добавляем в словарь новый код запрошенной позиции
    
12. 
    теперь программа отрабатывает очень быстро, и мы видим, что позиция (7, 17), которую мы хотели проверить, на самом деле выигрышная (её код 11); это значит, что ответ на вопрос задачи 21 – это 30.
    
13. 
    Ответ: 30.
    

Решение с помощью программы (рекурсия, 2-й вариант)

1. 
   введём константы: количество камней в первой куче, цель игры,
   

N1, TARGET = 7, 77

2. 
   количество камней, которые можно добавить, и коэффициент, на который можно умножить количество камней в любой куче:
   

KADD, KMUL = 1, 2

3. 
   определим вспомогательную функцию gameOver, которая возвращает истинное логическое значение (True), если игра окончена:
   

def gameOver( n1, n2 ):

return n1+n2 >= TARGET

4. 
   определим функцию win(n1,n2,byMove), которая возвращает истинное логическое значение (True), если в позиции (n1,n2) можно гарантированно выиграть не более чем за byMove ходов:
   

def win( n1, n2, byMove ):

if gameOver(n1, n2): return False

return lose( n1+KADD, n2, byMove-1 ) or \

lose( n1*KMUL, n2, byMove-1 ) or \

lose( n1, n2+KADD, byMove-1 ) or \

lose( n1, n2*KMUL, byMove-1 )

В первой строке проверяется условие окончания игры: если игра окончена, то тот, чья очередь ходить в этой позиции, проиграл:

if gameOver(n1, n2): return False

Игрок выигрывает в некоторой позиции не более чем за byMove ходов, если все его возможные ходы ведут в проигрышные (для соперника) позиции, причем при любом ходе соперник проигрывает не более чем за byMove-1 ходов:

return lose( n1+KADD, n2, byMove-1 ) or \

---

lose( n1*KMUL, n2, byMove-1 ) or \

lose( n1, n2+KADD, byMove-1 ) or \

lose( n1, n2*KMUL, byMove-1 )

Здесь вызывается функция lose(n1,n2,byMove), которую мы напишем далее. Она возвращает истинное логическое значение (True), если в позиции (n1,n2) игрок гарантированно проиграет не более чем за byMove ходов.

Обратите внимание на логическую операцию or: для выигрыша достаточно, чтобы хотя бы один ход создавал проигрышную позицию для соперника.

5. 
   функция lose выглядит так:
   

def lose( n1, n2, byMove ):

if gameOver(n1, n2): return True

if byMove == 0: return gameOver(n1, n2)

return win( n1+KADD, n2, byMove ) and \

win( n1*KMUL, n2, byMove ) and \

win( n1, n2+KADD, byMove ) and \

win( n1, n2*KMUL, byMove )

Сначала проверяется, не закончилась ли уже игра. Если это случилось, возвращается значение True: тот, кто получил такую позицию, проиграл.

Если уже не осталось ходов (byMove==0), результат работы функции равен False: игра окончена, а ходов уже нет.

В общем случае проверяем возможные ходы: если все они приводят к выигрышу соперника не более чем за byMove ходов, то позиция проигрышная, причем проигрыш наступит не позже, чем хода с номером byMove (дольше сопротивляться не получится).

Обратите внимание на логическую операцию and: для проигрыша необходимо, чтобы все ходы вели в выигрышную позицию для соперника.

6. 
   ответ на вопрос задания 19 строится так же, как было показано выше; для округления вверх используется функция ceil из модуля math:
   

from math import ceil

ans1 = min( ceil((TARGET-N1)/KMUL/KMUL),

ceil(TARGET-N1*KMUL*KMUL) )

7. 
   значения s, при которых выполняются условия заданий 20 и 21, находятся в цикле:
   

for s in range(18,TARGET-N1+1):

if win(N1, s, 2) and not win(N1, s, 1):

ans2.append(s)

if lose(N1, s, 2) and not lose(N1, s, 1):

ans3.append(s)

Массив ans2 содержит все значения s, при которых есть стратегия выигрыша в 2 хода, но нет стратегии гарантированного выигрыша за 1 ход; массив ans3 содержит все значения s, при которых тот, кто начинает игру, проигрывает за 2 хода, но не всегда проиграет за 1 ход.

8. 
   полная программа на Python:
   

N1, TARGET = 7, 77

KADD, KMUL = 1, 2

def gameOver( n1, n2 ):

return n1+n2 >= TARGET
def win( n1, n2, byMove ):

if gameOver(n1, n2): return False

return lose( n1+KADD, n2, byMove-1 ) or \

lose( n1*KMUL, n2, byMove-1 ) or \

lose( n1, n2+KADD, byMove-1 ) or \

---

lose( n1, n2*KMUL, byMove-1 )
def lose( n1, n2, byMove ):

if gameOver(n1, n2): return True

if byMove == 0: return False

return win( n1+KADD, n2, byMove ) and \

win( n1*KMUL, n2, byMove ) and \

win( n1, n2+KADD, byMove ) and \

win( n1, n2*KMUL, byMove )
from math import ceil

ans1 = min( ceil((TARGET-N1)/KMUL/KMUL),

ceil(TARGET-N1*KMUL*KMUL) )

ans2, ans3 = [], []

for s in range(18,TARGET-N1+1):

if win(N1, s, 2) and not win(N1, s, 1):

ans2.append(s)

if lose(N1, s, 2) and not lose(N1, s, 1):

ans3.append(s)
print("--- Ответы ---")

print("19. ", ans1)

print("20. ", sorted(ans2))

print("21. ", ans3)

Решение на языке PascalABC.NET:

1. 
   в целом решение повторяет приведённое выше решение на Python
   
2. 
   для хранения уже полученных результатов используется словарь memory, в котором каждой паре чисел, задающих количество камней в двух кучах (тип tuple) сопоставляется целое число – оценка позиции:
   

type tuple = (integer, integer);

const TARGET = 77;

var memory: Dictionary;

function gameResult( x, y: integer ): integer;

begin

if (x, y) in memory then begin

result := memory[(x,y)];

exit;

end;

if x+y >= TARGET then begin result := 0; exit; end;

var next := | gameResult(x+1,y),

gameResult(x,y+1),

gameResult(2*x,y),

gameResult(x,2*y)|;

var negative := next.Where(x->x<=0).ToArray;

if negative.Length > 0 then

result := - negative.Max + 1

else

result := - next.Max;

memory[(x,y)] := result;

end;
begin

var X:= 7;

memory := new Dictionary;

for var s:=TARGET-X-1 downto 1 do

Println( s, gameResult(x,s) );

end.
Решение с помощью программы (динамическое программирование, А. Сидоров)

1. 
   вместо рекурсии можно применить динамическое программирование, где вместо словаря results используется двухмерный массив:
   

TARGET = 77

results = [[0]*2*TARGET for i in range(2*TARGET)]

for x in range(TARGET-1,0,-1):

for y in range(TARGET-x-1,0,-1):

nextCodes = [ results[x+1][y], results[2*x][y],

results[x][y+1], results[x][2*y]]

negative = [с for с in nextCodes if с <= 0]

if negative:

results[x][y] = -max(negative) + 1

else:

results[x][y] = -max(nextCodes)
N1 = 7

for S in range(TARGET-N1-1,0,-1):

print( "{:d} {:d}".format(S, results[N1][S]) )

Эта программа для каждого значения S выводит оценку позиции. Положительные значения K означают выигрыш: Петя выиграет за K ходов. Отрицательные значение (-K): Ваня гарантированно выиграет не позднее, чем своим K-м ходом.

2. 
   Ответ: 30.
   

Решение с помощью электронных таблиц (А. Кабанов)

1. 
   Для начала отметим комбинации камней, из которых игрок побеждает своим первым ходом. Составим таблицу, в которой по вертикали отметим камни в первой куче камней (начиная с 7), а по горизонтали – во второй куче камней (начиная с 1).
   

---

2. 
   Для каждой пары рассчитаем максимальное число камней, которое может получить игрок за один ход. Для этого необходимо большую из куч умножить на два. В ячейке B2 запишем формулу =МАКС(2*$A2+B$1;$A2+2*B$1) и заполним ей всю нашу таблицу. Далее с помощью условного форматирования пометим ячейки, в которых сумма не менее 77 (условие выигрыша).
   

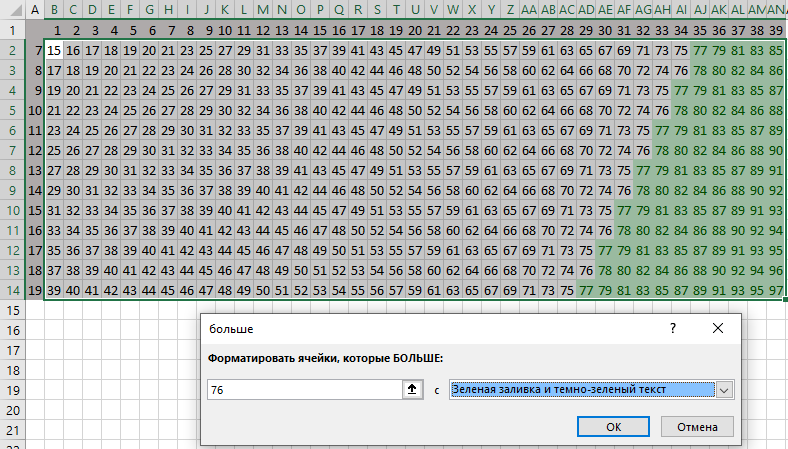
Решение 19 задания:

3. 
   Для решения 19 задания рассмотрим две ситуации:
   

а) Петя умножает вторую кучу на 2, а Ваня выигрывает первым ходом. Ход Пети имеет вид (7;S) →(7;2S). Ваня будет выигрывать первым ходом, если 2S ≥35 (см. таблицу) или S≥18.

б) Петя умножает первую кучу на 2, а Ваня выигрывает первым ходом. Ход Пети имеет вид (7;S) →(14;S). Ваня будет выигрывать первым ходом, если S ≥32 (см. таблицу).

4. 
   Нетрудно видеть, что минимальное подходящее значение S равно 18.
   
5. 
   Ответ: 18.
   

Решение 20 задания:

6. 
   Для начала найдём проигрышные значения (при любой игре побеждает следующий игрок). Рассмотрим комбинации (K; S) из которых каждый ход вида (K; S+1) (K+1; S) (2K; S) (K; 2S) попадает в выигрышные позиции.
   

7. 
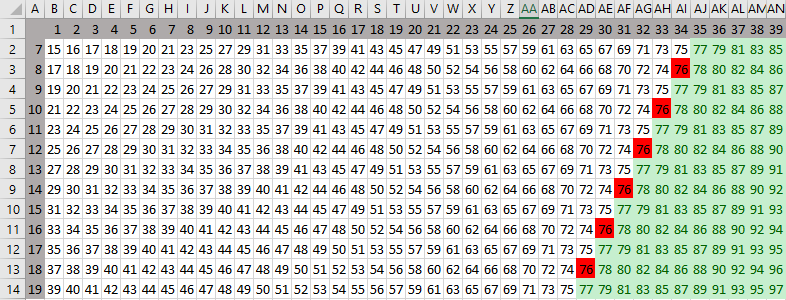
   Петя будет гарантированно побеждать своим вторым ходом, если его первый ход попадает в отмеченные проигрышные значения.
   
8. 
   Рассмотрим ситуации, когда победный ход Пети (K+1;S) или (K;S+1). Отметим в таблице ячейки, из которых возможны такие ходы.
   

9. 
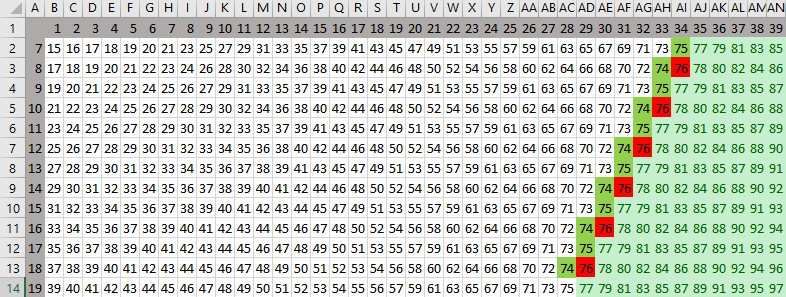
   Рассмотрим ситуации, когда победный ход Пети (2K; S) или (K;2S). Выпишем все проигрышные позиции:
   

(8;34) (10;33) (12;32) (14;31) (16;30) (18;29) …

10. 
    Для каждой из них выпишем, позиции с вдвое меньшим числом камней в одной из куч (если такая позиция возможна):
    

(8;34) – (8;17)

(12;32) – (12;16)

(14;31) – (7;31)

(16;30) – (8;30) (16;15)

(18;29) – (9;29)

11. 
    Также отметим их на таблице (остальные по необходимости добавляются по аналогии)
    

---

12. 
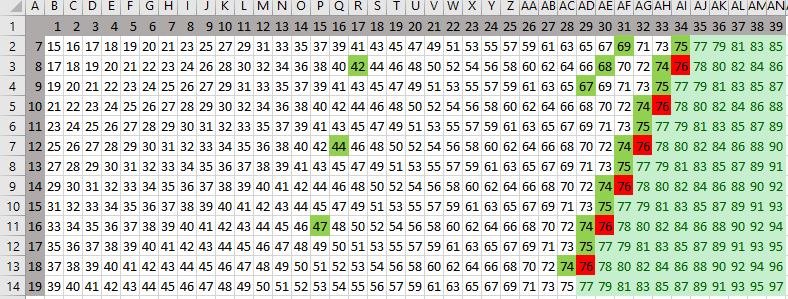
    Интерес представляют значения, где первая куча равна 7, поэтому:
    
13. 
    Ответ: 31 34.
    

Решение 21 задания:

14. 
    Рассмотрим комбинации вида (7;S), ходы (K+1;S) и (K;S+1) из которых попадает в выигрышные позиции. По таблице видно, что это (7;33) и (7;30). Проверим их:
    

– Из (7;33) Петя может сходить в (7;34) (8;33) – победа Вани 2 ходом и (7;66) (14;33) – победа Вани 1 ходом.

– Из (7;30) Петя может сходить в (7;31) (8;30) (14;30) – победа Вани 2 ходом и (7;62)– победа Вани 1 ходом.

15. 
    Оба значения подходят и наименьшее из этих значений 30.
    
16. 
    Ответ: 30.
    

Решение с помощью программы: имитация решения в электронных таблицах (Д. Муфаззалов)

Если трудно разобраться в рекурсивном алгоритме или динамическом программировании, можно написать более простую программу, имитирующую решение в электронных таблицах.

1. 
   Вместо таблицы будем использовать двумерный массив:
   

n = 69
target = 77
a = [["--"] * target * 2 for i in range(target * 2)]

2. 
   Найдем игровые ситуации, из которых можно выиграть за 1 ход:
   

for i in range(1,target):
for j in range(1,target):
if (i + j + 1 >= target or

i * 2 + j >= target or

i + 2 * j >= target) and i + j < target:
a[i][j] = "V1"

3. 
   Введем функцию, возвращающую множество игровых ситуаций, которые можно получить из текущей игровой ситуации:
   

def f(i,j):

return set([a[i][j+1], a[i+1][j],

a[i*2][j], a[i][j*2]])

4. 
   Найдем игровые ситуации, из которых игрок проигрывает за один ход:
   

for i in range(1,target):
for j in range(1,target):
if a[i][j] == "--" and f(i,j)=={'V1'}:

a[i][j] = "P1"

5. 
   Найдем игровые ситуации, из которых игрок выигрывает за 2 хода:
   

for i in range(1,target):
for j in range(1,target):
if a[i][j] == "--" and ("P1" in f(i,j)):

a[i][j] = "V2"

6. 
   Найдем игровые ситуации, из которых игрок проигрывает за один или два хода:
   

for i in range(1,target):
for j in range(1,target):
if a[i][j] == "--" and (f(i,j) == {'V1', 'V2'}):

a[i][j] = "P2"

7. 
   Выведем результаты расчетов:
   

for i in range(n+1):

print( "%3d" % i, end='' )
print()
for i in range(1,n):
print( "%3d" % (i ), end='')
for j in range(1,n):

print( "%3s" % a[i][j], end='')
print()

8. 
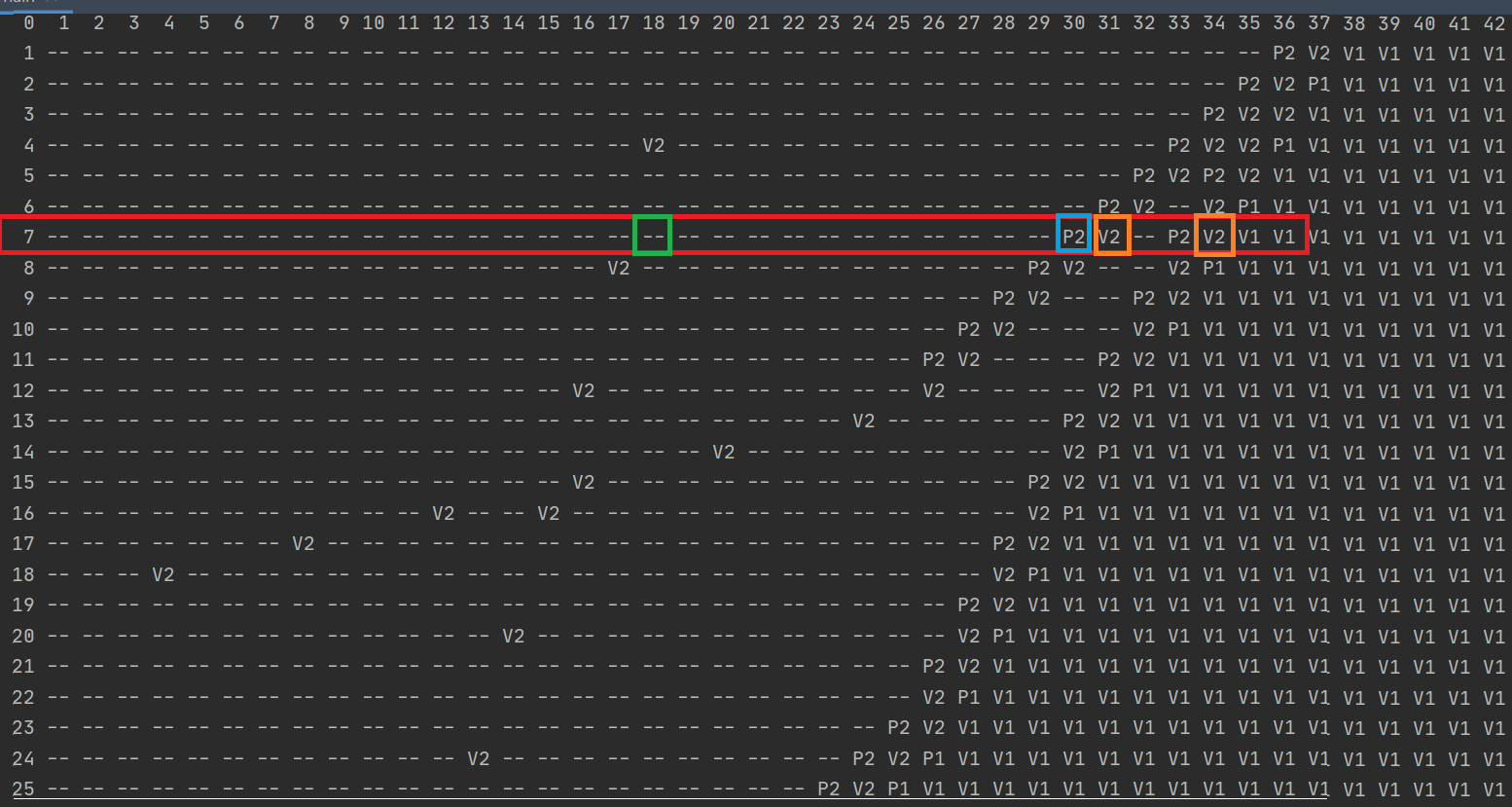
   Ответы к заданиям можно получить рассуждениями, приведенными выше.
   Полная программа:
   

n = 69
tar = 77
a = [["--"] * tar * 2 for i in range(tar * 2)]
def f(i,j):

---

Смотрите также файлы

• Экология мірді соып тран жрегі!.docx

• ТАырып Инвестициялы саясат туралы ым Инвестицияны экономикалы мазмны мен рлі Инвестиция термині латынны invest сзінен аударанда салым салу.docx

• Балаларды жасы 5 жас Жоспар андай кезеге жасалды (айды, жылды крсету).docx

• Математическая грамотность (8 класс) Характеристики заданий и система оценивания.docx

• Бастауыш, ши бауырса, самса мелкие, булочки мелкие, жеті нан.docx