Файл: Автоматического управления, система автоматического регулирования, передаточные функции, устойчивость системы, коррекция системы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 51
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
На рисунке 4.2 представлен программный код, реализованный в среде Scilab. Он предназначен для расчета передаточных функций звеньев.
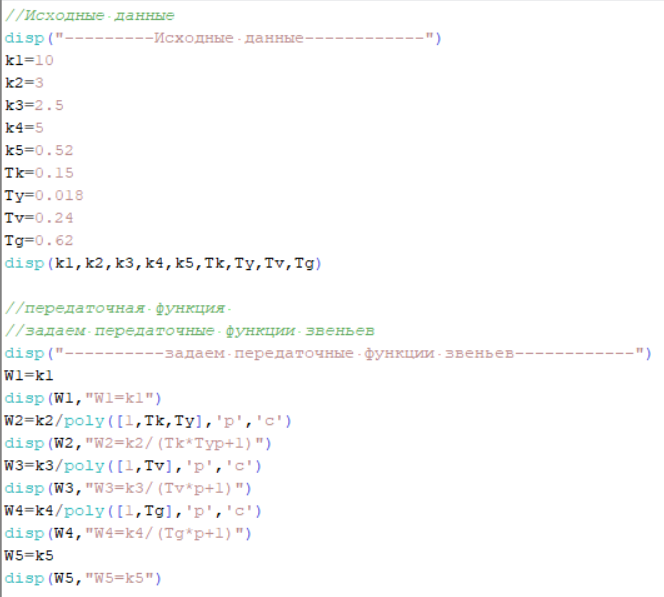
Рисунок 4.2 – Программный код, реализованный в среде Scilab
5 Передаточные функции системы
Передаточная функция разомкнутой системы находится как произведение передаточных функций пяти последовательно соединённых инерционных звеньев, описанных в предыдущем разделе:
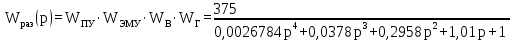 | (5.1) |
Передаточная функция цепи обратной связи по задающему воздействию:
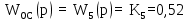 | (5.2) |
Передаточная функция замкнутой системы:
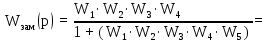 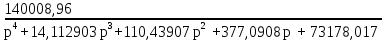 | (5.3) |
На рисунке 5.1 представлен программный код, реализованный в среде Scilab. Он предназначен для расчета передаточных функций системы.
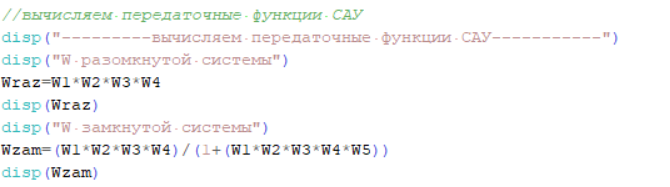
Рисунок 5.1 – Программный код для вычисления передаточных функций САУ
6 Проверка системы на устойчивость
Чтобы проверить систему на устойчивость, найдем корни характеристического уравнения. Если все корни характеристического уравнения отрицательны, то система устойчива.
Характеристическое уравнение для разомкнутой системы:
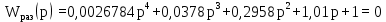 | (6.1) |
Корни характеристического уравнения (6.1):
-4,1666667 + 6,1801654i
-4,1666667 – 6,1801654i
-4,1666667
-1,6129032
Все корни отрицательны, следовательно, система устойчива.
Характеристическое уравнение для замкнутой системы:
| Wзам(p) = 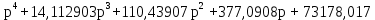 =0 =0 | (6.2) |
Корни характеристического уравнения (6.2):
-14,750166 + 12,03907i
-14,750166 – 12,03907i
7,6937143 + 11,9446i
7,6937143 – 11,9446i
Не все корни отрицательны, следовательно, система не устойчива.
На рисунке 6.1 представлен программный код, предназначенный для решения характеристических уравнений.

Рисунок 6.1 – Программный код, предназначенный для решения характеристических уравнений
Построим переходную характеристику системы. Она изображена на рисунке 6.2. На рисунке 6.3 представлен необходимый для этого программный код.
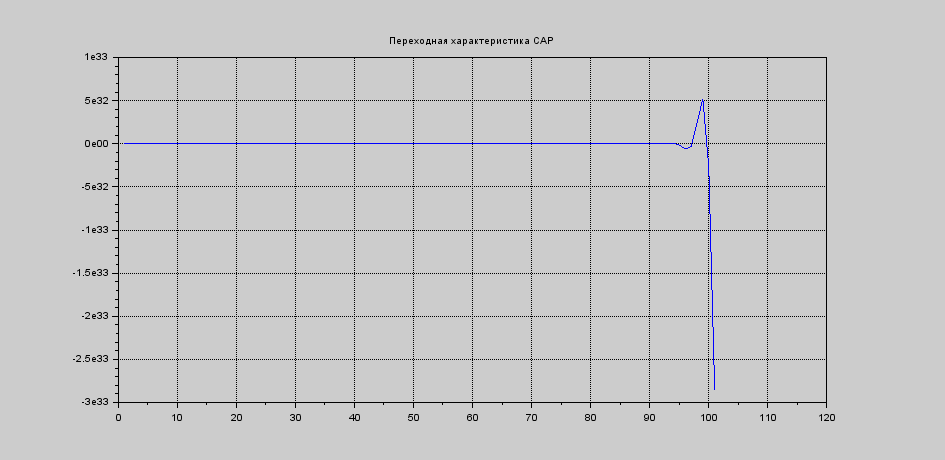
Рисунок 6.2 - Переходная характеристика системы

Рисунок 6.3 – Программный код для построения переходной характеристики
Для более точной проверки системы на устойчивость, воспользуемся критериями устойчивости.
6.1 Критерий Найквиста
Исследование системы на устойчивость по критерию Найквиста производится путем построения амплитудно-фазовой характеристики разомкнутой системы. Для того чтобы система была устойчива, необходимо и достаточно чтобы график не охватывал точку (−1; 0) на комплексной плоскости. Построим годограф Найквиста (рис. 6.4). Отметим проекции точки (-1;0) на оси для того, чтобы увидеть, выполняется условие или нет. На рисунке 6.5 представлен необходимый для построения АФХ код.
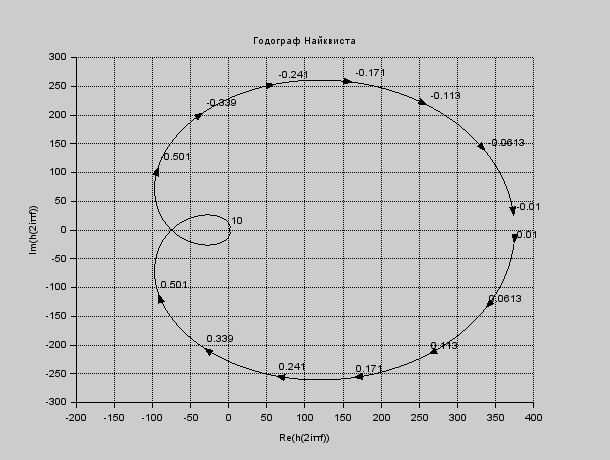
Рисунок 6.4 – Годограф Найквиста
Система является устойчивой, т.к. данный график не пересекает точку (-1;0).

Рисунок 6.5 – Программный код для построения годографа Найквиста
6.2 Критерий Михайлова
Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до ω начинался на вещественной оси, и проходил последовательно против часовой стрелки 4 квадрантов комплексной плоскости. На рисунке 6.6 представлен годограф Михайлова, на рисунке 6.7 – необходимый для его построения программный код.
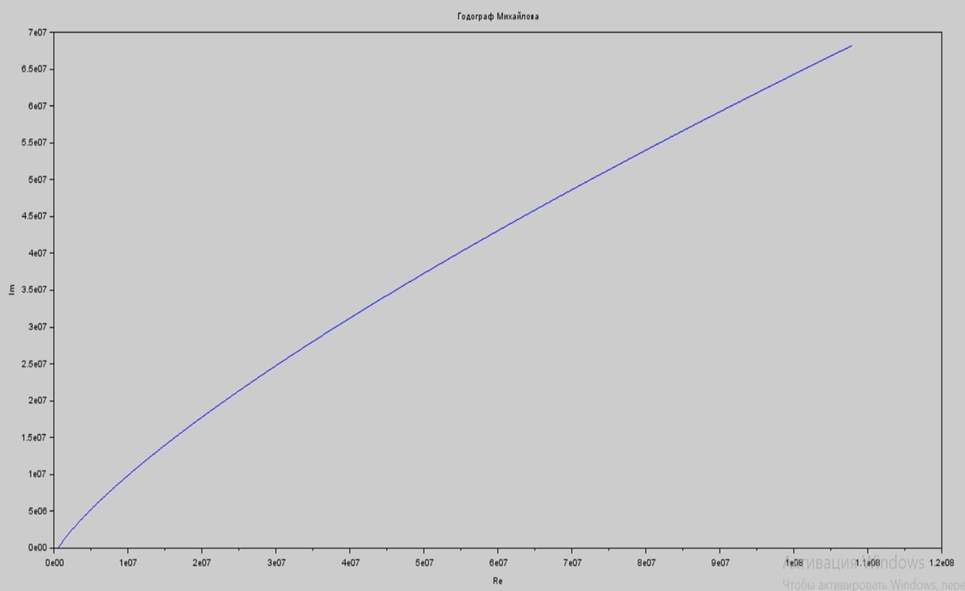
Рисунок 6.6 – Годограф Михайлова
Условие устойчивости не выполняется, следовательно, система неустойчива.

Рисунок 6.7 – Программный код для построения годографа Михайлова
6.3 Критерий Гурвица
Для того чтобы система была устойчива, необходимо и достаточно, чтобы определители Гурвица, составленные из коэффициентов ее характеристического уравнения, при a0 > 0 были также больше нуля. Характеристическое уравнение замкнутой системы определяется как приравненный нулю знаменатель передаточной функции замкнутой же системы.
Характеристическое уравнение:
| Wзам(p) =  =0 =0 | (6.3) |
Коэффициенты:
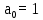 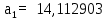 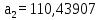 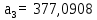 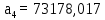 | (6.4) |
Первое условие выполняется, так как а0 > 0. Вычислим определители:
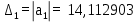 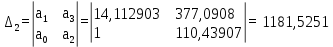 | (6.5) |
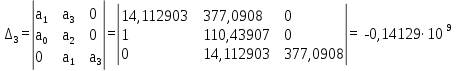 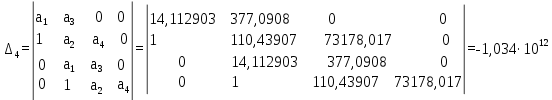 | |
Т.к. не все определители положительные, то система не устойчива. На рисунке 6.8 представлен используемый для расчета программный код.
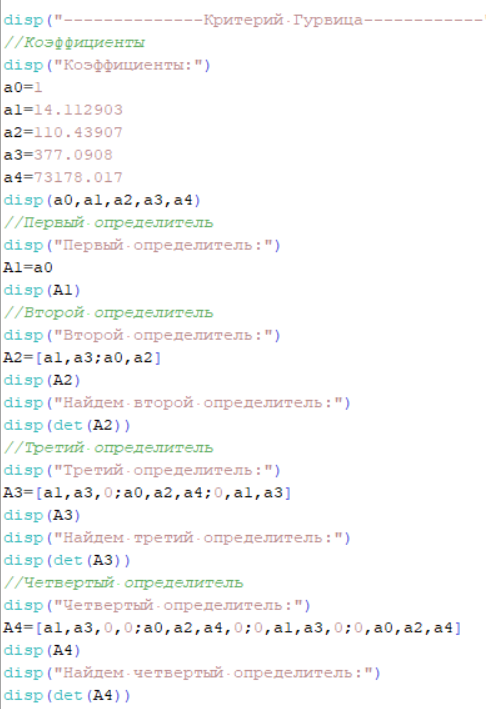
Рисунок 6.8 – Программный код для расчета определителей по критерию Гурвица
6.4 Критерий Рауса
Для того чтобы система была устойчива, необходимо и достаточно чтобы все коэффициенты передаточной функции замкнутой системы, находящиеся в первом столбце таблицы Рауса были положительны.
Характеристическое уравнение для замкнутой системы:
| Wзам(p) =  =0 =0 | (6.6) |
В таблице 6.1 представлены коэффициенты характеристического уравнения для замкнутой системы.
Таблица 6.1 – Таблица Рауса
| ri | | 1 | 2 | 3 |
| - | 1 | 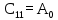 | 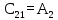 | 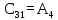 |
| - | 2 | 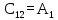 | 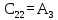 | 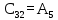 |
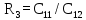 | 3 | 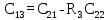 | 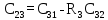 | 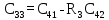 |
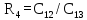 | 4 | 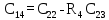 | 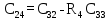 | 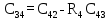 |
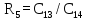 | 5 | 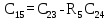 | 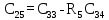 | 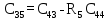 |
Рассчитаем коэффициенты из таблицы 6.1. Полученные результаты представлены в таблице 6.2.
Таблица 6.2 – Результаты вычислений таблицы Рауса
| ri | | 1 | 2 | 3 |
| - | 11 | 1 | 110,43907 | 73178,017 |
| - | 22 | 14,112903 | 377,0908 | 0 |
| 0,071 | 23 | 83,719 | 73180 | 0 |
| 0,169 | 44 | -1960 | 0 | 0 |
| -0,07001 | 55 | 73180 | 0 | 0 |
Среди коэффициентов первого столбца есть те, которые меньше нуля. Условие не выполняется, следовательно, система не устойчива.
7 Коррекция устойчивости системы
Построим ЛАЧХ исходной системы. На рисунке 7.1 изображена ЛАЧХ разомкнутой системы. На рисунке 7.2 изображена ЛАЧХ замкнутой системы. На рисунке 7.3 представлен необходимый для их построения программный код.
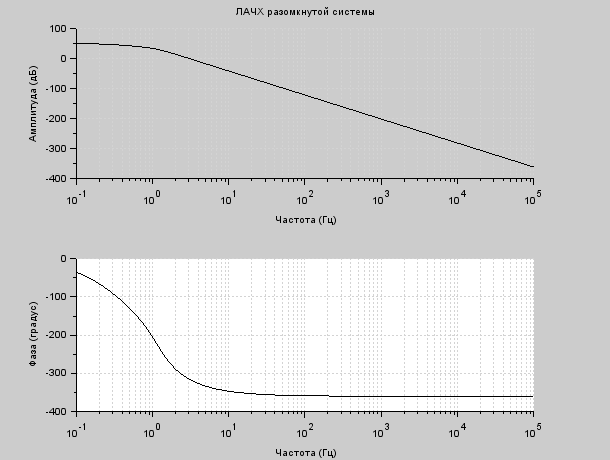
Рисунок 7.1 – ЛАЧХ разомкнутой системы
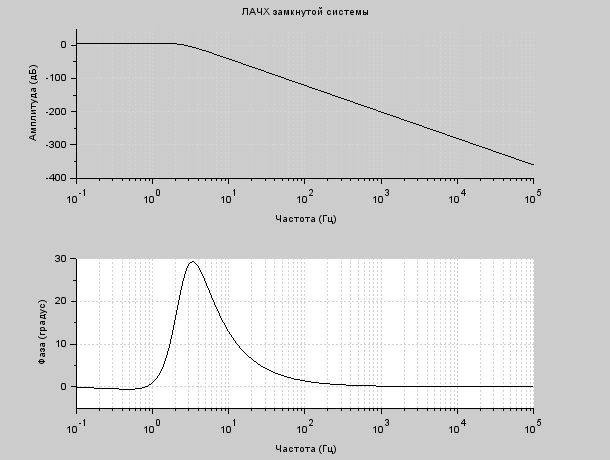
Рисунок 7.2 – ЛАЧХ замкнутой системы

Рисунок 7.3 – Программный код для построения исходной ЛАЧХ
Построим желаемую ЛАЧХ. Найдем частоту среза с помощью номограмм Солодовникова, используя исходные данные tрег = 0,72 с, m = 50 %. На рисунке 7.4 представлена зависимость времени регулирования и величины перерегулирования от значения функции. На рисунке 7.5 изображена зависимость запасов устойчивости от управляющего воздействия.
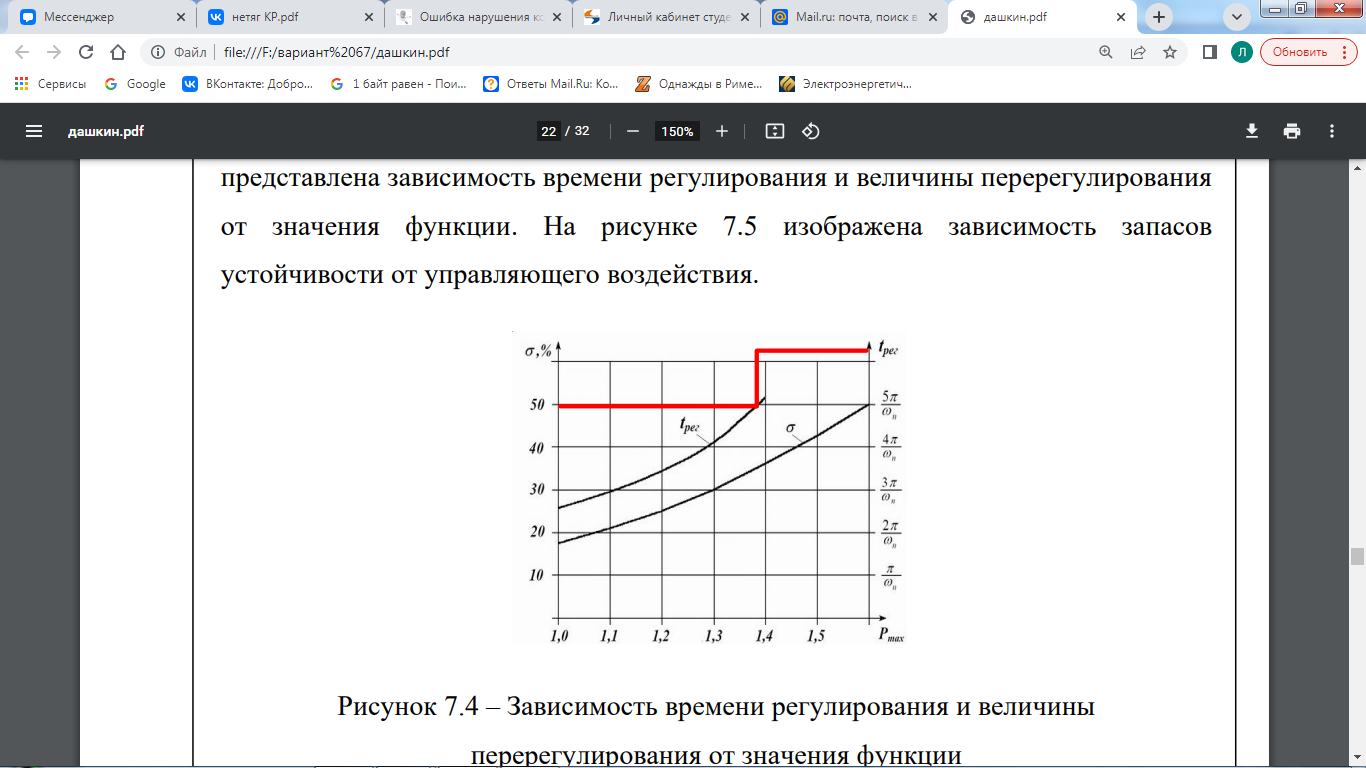
Рисунок 7.4 – Зависимость времени регулирования и величины перерегулирования от значения функции
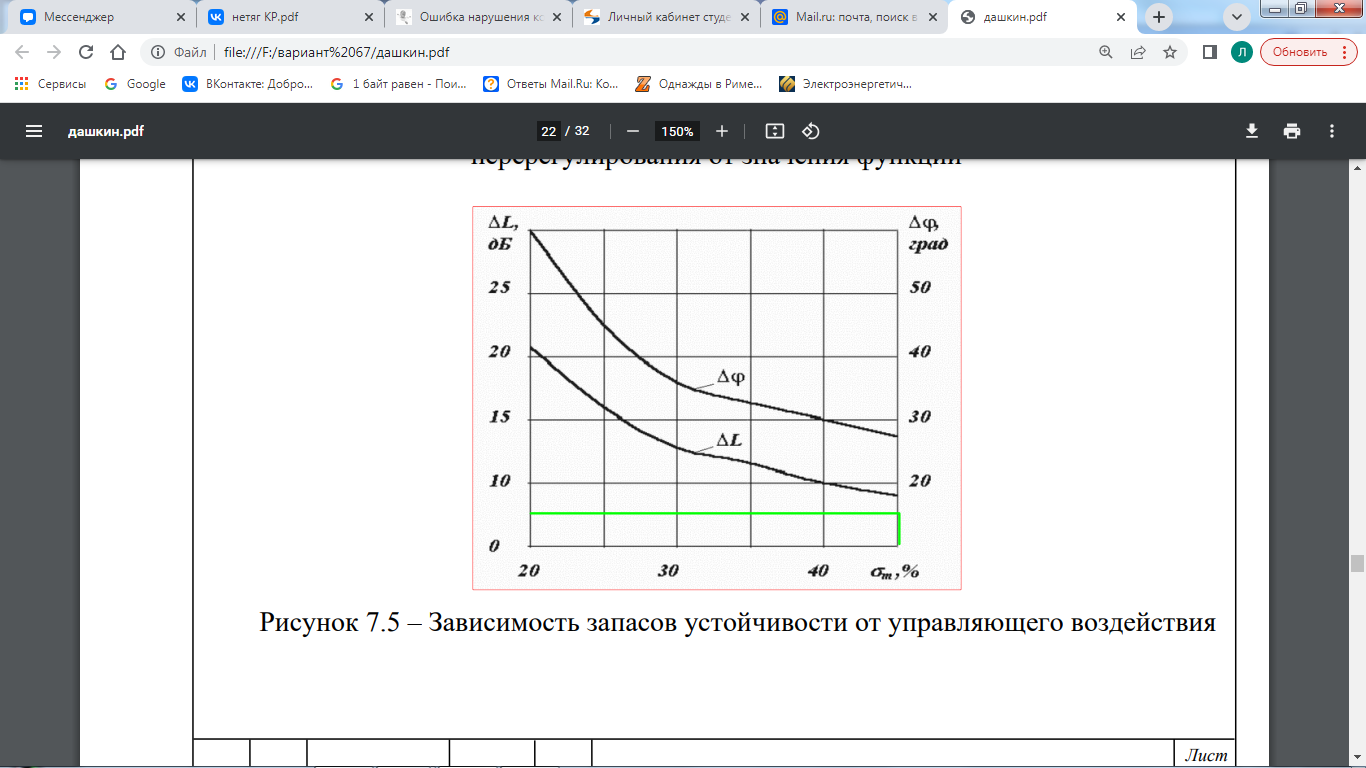
Рисунок 7.5 – Зависимость запасов устойчивости от управляющего воздействия
Используя графики (рис. 7.4 и рис. 7.5) и программный код, изображенный на рис. 7.6, определим коэффициент усиления в дБ и частоту среза. Построим график желаемой ЛАЧХ (рис. 7.8). Для этого необходимо при помощи номограмм Солодовникова построить низкочастотную, среднечастотную и высокочастотную части ЛАЧХ. Коэффициент усиления определяется из числителя выражения (5.1): K = 375