Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Кафедра общей и технической физики

Лабораторная работа №13

Изучение магнитного поля тока


Выполнил студент группы: ПГ-99 Коновалов С.Ю.

Проверил: доцент Корольков А.П.

Санкт-Петербург

2000

Цель работы:

Изучить магнитное поле, создаваемое током, текущим по прямоугольной рамке. Измерить с помощью индукционного датчика, соединенного с ламповым вольтметром, магнитное поле нижнего участка этой рамки при различных расстояниях до него. Построить график зависимости магнитного поля от расстояния и сравнить его с теоретическим, полученном на основании закона Био- Савара- Лапласа.

Общие сведения:

Вокруг проводника, по которому протекает электрический ток, существует магнитное поле, каждая точка которого характеризуется вектором напряженности (рис.1). Вектор может быть найден как сумма векторов напряженности , создаваемых каждым малым участком проводника с током:



Согласно закону Био- Савара- Лапласа

,

где I- сила тока в проводнике; - вектор, имеющий длину отрезка и направленный вдоль тока; - радиус- вектор, проведенный из элемента

---

в рассматриваемую точку Р.

Вектор направлен перпендикулярно плоскости, проведенной через и , и связан с направлением тока правилом правого винта:

.

Для прямолинейного проводника с током конечной длины (рис.2) все , создаваемые отдельными элементарными участками в точке поля Р, направлены в одну сторону ( перпендикулярно плоскости чертежа). В этом случае напряженность магнитного поля в точке Р может быть найдена интегрированием:

.

Произведем вычисления в СИ, найдем, что

, (1)

где - кратчайшее расстояние от точки Р до проводника с током; - углы между крайними элементами проводника и соответствующими радиус- векторами РА и РВ.

Рис.1 Рис.2
Если определить напряженность в точках, расположенных на перпендикуляре, восстановленном в середине проводника, то



(2)

С учетом выражения (2) формулу (1) можно записать в виде

(3)

Для исследования зависимости напряженности магнитного поля прямолинейного тока от расстояния до проводника применяется следующий метод. Прямоугольная, вытянутая по вертикали рамка ABCD (рис.3) присоединяется к генератору переменной ЭДС. По рамке течет переменный ток, изменяющийся с течением времени t, следующим образом:

,

где

---

- амплитудное (максимальное) значение тока в цепи; - угловая частота переменного тока.

Вокруг проводника создается переменное магнитное поле напряженностью

,

где - амплитудное значение напряженности.

Маленькая плоская катушка- это индукционный датчик (ИД), содержащий N витков, помещается в точку Р поля так, чтобы ее центр совпал с этой точкой. По законам электромагнитной индукции в катушке возникает ЭДС

;

где Ф- магнитный поток, пронизывающий каждый поток катушки. Известно, что

,

где - магнитная постоянная; - магнитная проницаемость среды, в которой создано магнитное поле, в нашем случае , т.к. поле создано в воздухе; S- площадь измерительной катушки ИД. Поэтому можно записать

(4)

Обозначив

, (5)

получим

(6)

Равенство (5) показывает, что пропорционально . Следовательно, рассчитав , можно рассчитать значение в любой точке поля. Т.к.

---

(здесь -действующее значение ЭДС), то

(7)


Схема установки

Рис.3

Расчетные формулы



где d-ширина участка АВ рамки.




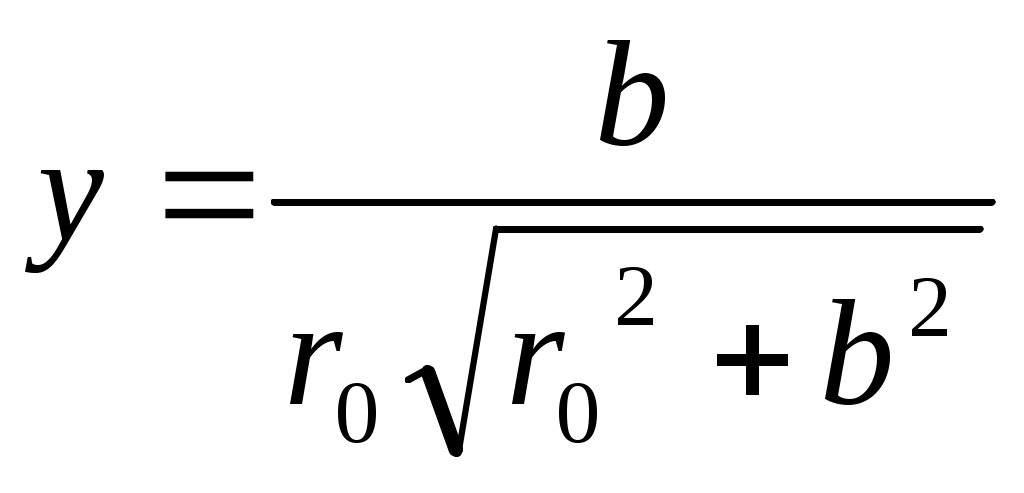
Формула погрешности
=

Таблица измерений

							H
1	0.01	0.01	0.001	0.110	0.005	95	11*
3		0.02		0.072		48	7.0*
5		0.03		0.054		32	5.2*
7		0.04		0.046		24	4.5*
9		0.05		0.032		19	3.1*
11		0.06		0.026		15	2.5*
13		0.07		0.023		13	2.2*
15		0.08		0.020		11	1.9*
17		0.09		0.018		9	1.8*
19		0.10		0.017		8	1.7*
21		0.11		0.016		7	1.5*
23		0.12		0.016		6	1.5*
25		0.13		0.015		6	1.4*
27		0.14		0.014		5	1.4*
29		0.15		0.014		4	1.3*

---

N=300 d=1.1см=0,011м

S=78 =0,078 =2 *63*1 1/сек

B=13.5см=0,135м =4 *1 Гн/м

=1

Расчет погрешности измерений

= = 4,8*

График зависимости


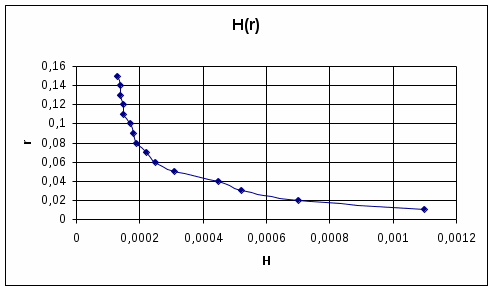
График зависимости Н(у)




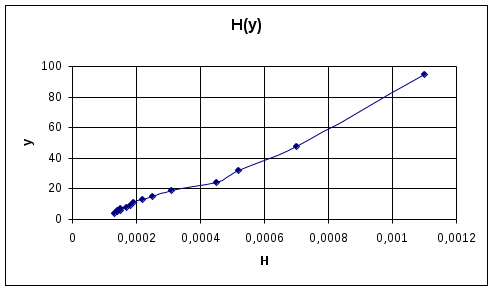
Вывод

Изучил магнитное поле, создаваемое током, текущим по прямоугольной рамке. Измерил с помощью индукционного датчика, соединенного с ламповым вольтметром, магнитное поле Н нижнего участка этой рамки при различных расстояниях до него. Построил график зависимости магнитного поля от расстояния и сравнил его с теоретическим, полученным на основании закона Био- Савара- Лапласа.

---

Смотрите также файлы

• азастан республикасы ылым жне жоАРы білім министрлігі.docx

• Тема 4 Управление и организация.docx

• Программа Практическая биология.docx

• .docx

• Компьютерная сеть оао первоуральское рудоуправление.pdf