Файл: Учебнометодическое пособие по дисциплине геодезическая астрономия с основами астрометрии методические указания по выполнению контрольной работы 1 для студентов заочной формы обучения по специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 135
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский государственный университет геодезии и картографии» (МИИГАиК)
Учебно-методическое пособие по дисциплине
ГЕОДЕЗИЧЕСКАЯ АСТРОНОМИЯ С ОСНОВАМИ АСТРОМЕТРИИ:
методические указания по выполнению контрольной работы № 1
для студентов заочной формы обучения по специальности
21.05.01 Прикладная геодезия
| Составители: | Суслин В.И., старший преподаватель Абросимова Е.В. |
| | Рекомендовано к использованию в учебном процессе МИИГАиК решением Методического совета университета (протокол № от «___» ____________ 2020г.) |
| Рецензенты: | Литвиненко М.В., декан факультета дистанционных форм обучения МИИГАиК, д.п.н. Баранов В.Н., зав. кафедрой геодезии и геоинформатики ФБГОУ ВО «Государственный университет по землеустройству», д.т.н., профессор |
Москва 2020 г.
Оглавление
| | Стр. |
| Введение. | 3 |
| Задание № 1. Выборка звёзд. Построение чертежа небесной сферы. Положения звёзд в кульминациях. | 4 |
| Задание № 2. Решение практических задач на сфере. | 10 |
| Задание № 3. Вычисление видимых координат истинного Солнца и уравнения времени. | 15 |
| Задание № 4. Переход от среднего солнечного времени к звёздному и обратно. | 18 |
| Задание № 5. Интерполирование видимых координат близполюсных звёзд. | 21 |
| Задание № 6. Интерполирование видимых координат обычных звёзд. | 25 |
| Задание № 7. Интерполирование видимых координат звёзд по алгебраической системе формул. | 29 |
| Приложение. Основные формулы сферической тригонометрии. | 35 |
| Список литературы. | 38 |
Введение
По учебному плану для студентов заочной формы предусматривается выполнение контрольной работы по курсу «Геодезическая астрономия», которую студенты выполняют самостоятельно до прибытия на сессию и присылают преподавателю на проверку.
По результатам самостоятельной учебно-познавательной деятельности в ходе выполнения контрольной работы студент должен:
| Знать | Основные формулы сферической тригонометрии. Основные точки и круги небесной сферы. Системы координат и системы измерения времени. Понимать сущность и порядок учёта основных редукций в координаты звёзд. Понимать сущность зенитальных и азимутальных методов астрономических определений. |
| Уметь | Выполнять выборку звёзд для решения конкретных задач. Осуществлять переход между разными системами измерения времени. Интерполировать координаты Солнца, звёзд и основных редукций. Производить обработку журналов наблюдений и вычислять координаты пункта земной поверхности и азимута направления различными методами. |
| Владеть | Математическим аппаратом, применяемым в сферической астрономии. |
Порядок допуска к защите контрольной работы во время очных занятий на сессии:
| Результат проверки | Действия студента |
| Работа допущена к защите без исправлений | Сделав исправления в работе, где это указано преподавателем, студент не присылает повторно работу на проверку, а приносит исправленную работу на очные занятия в распечатанном виде для защиты. |
| Работа допущена к защите с исправлениями | |
| Работа не допущена к защите | Сделав исправления в работе, где это указано преподавателем, студент присылает работу на проверку повторно, до тех пор, пока работа не будет допущена к защите без исправлений или с незначительными исправлениями. |
Задание № 1.
1.1. Выборка звёзд.
1.2. Построение чертежа небесной сферы.
1.3. Положения звёзд в кульминациях.
-
Выборка звёзд.
Исходные данные
: № - номер варианта, широта пункта
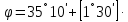 №.
№.Номер варианта для студентов ФДФО определяется по последним двум цифрам учебного шифра следующим образом: № варианта = шифр – n·30, где n (целая часть) = шифр/30). Если последние две цифры учебного шифра меньше или равны 30, то эти две цифры и образуют номер варианта. Если последние цифры шифра равны 0, то номер варианта № = 1.
Из таблиц «Средние места звёзд» Астрономического Ежегодника (АЕ), имеющегося года выпуска (но не старше 2006 г.) выбрать десять звёзд, относящихся к различным областям небесной сферы:
1) две незаходящих, 2) две невосходящих,
3) две восходящих и заходящих (одна звезда должна иметь положительное склонение, другая - отрицательное),
4) две проходящих через первый вертикал над горизонтом данного пункта и
5) две имеющих элонгацию.
Для каждой звёзды указывать номер страницы АЕ, откуда сделана выписка.
Разность прямых восхождений звёзд
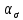 , удовлетворяющих каждому условию, должна быть около 12 часов (± 30 минут).
, удовлетворяющих каждому условию, должна быть около 12 часов (± 30 минут). Если для выборки звёзд из таблицы «Средние места звёзд» будет недостаточно данных для выполнения всех условий, тогда дополнительно можно воспользоваться таблицей «Средние места близполюсных звёзд» АЕ на тот же год.
Условия выбора звёзд.
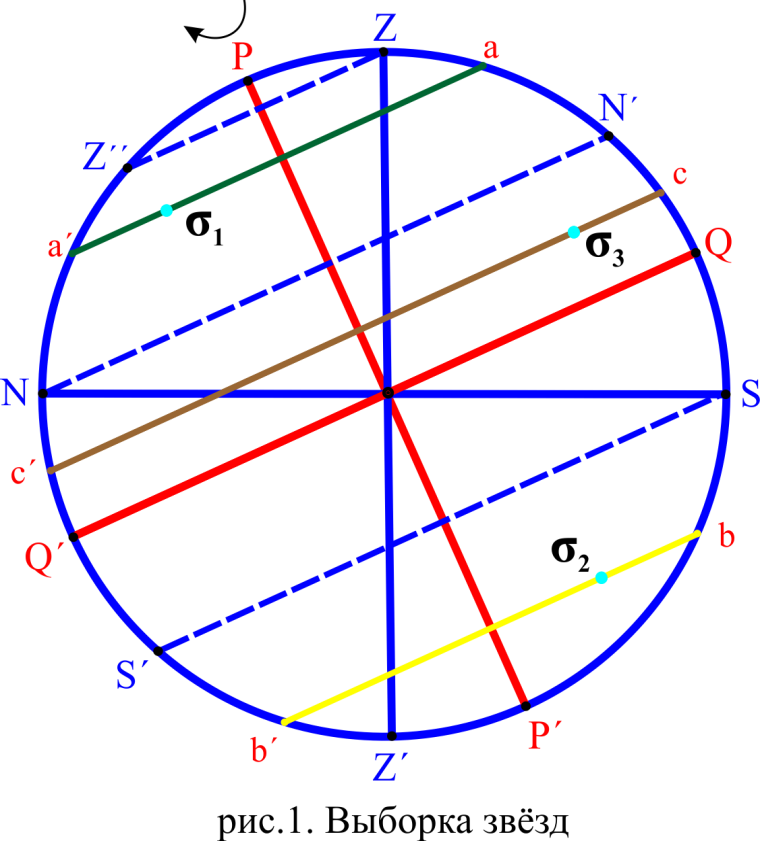 1) Незаходящие звёзды: суточные параллели не должны опускаться ниже линии горизонта NS, область неба NPZN΄ (пример: - см.рис.1 звезда
1) Незаходящие звёзды: суточные параллели не должны опускаться ниже линии горизонта NS, область неба NPZN΄ (пример: - см.рис.1 звезда 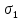 , суточная параллель aa׳).
, суточная параллель aa׳). 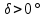 ,
, 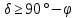 .
.2) Невосходящие звёзды: суточные параллели не должны подниматься выше линии горизонта NS, область неба SP΄Z΄S΄ (пример: - см.рис.1 звезда
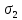 , суточная параллель bb׳).
, суточная параллель bb׳). 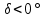 ,
, 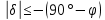 .
.3) Восходящие и заходящие звёзды: включают область неба между параллелями NN΄ и SS΄ (пример: - см.рис.1 звезда
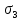 , суточная параллель cc׳).
, суточная параллель cc׳).а)
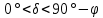 ,
,б)
 ,
, 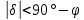 , или
, или 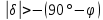 .
.4) Звёзды, проходящие через первый вертикал над горизонтом (см.рис.2).
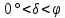 .
.Элонгирующие звёзды (см.рис.3): область неба ZZ΄΄. Условие элонгации для северного полушария:
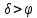 , то есть верхняя кульминация светила происходит к северу от зенита. Для южного полушария условие элонгации не меняется:
, то есть верхняя кульминация светила происходит к северу от зенита. Для южного полушария условие элонгации не меняется: 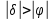 , так как в южном полушарии широты отрицательные.
, так как в южном полушарии широты отрицательные.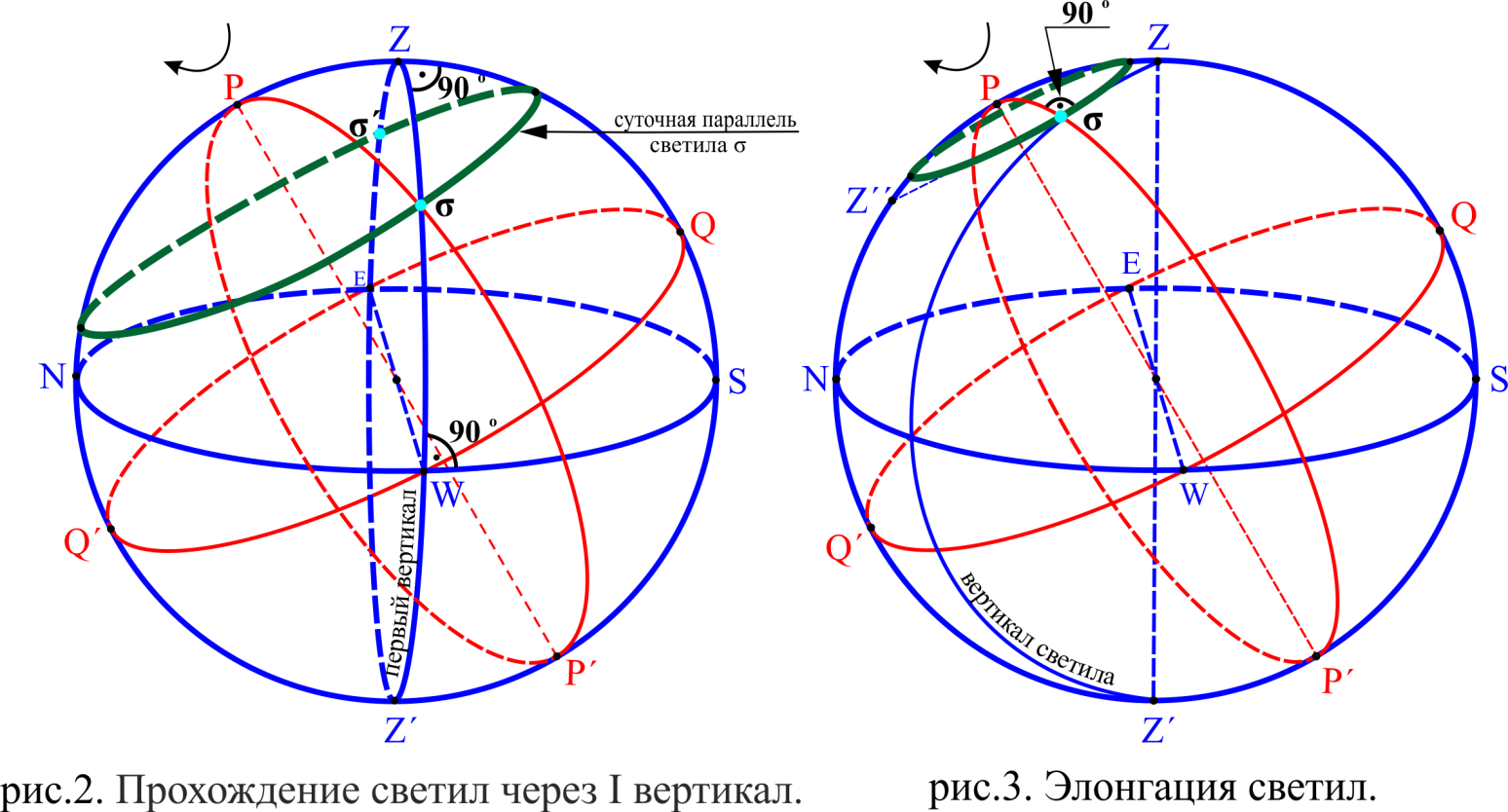
1.2. Построение чертежа небесной сферы.
Построить плоский чертёж небесной сферы для пункта с широтой φ (см. п.1.1.) и указать на нём суточные параллели выбранных звёзд. Рекомендуемый размер сферы: диаметр не менее 10 см. Номер звезды по АЕ указывать рядом с её суточной параллелью.
Чертёж выполнить с помощью любой графической программы или классическим способом (карандаш, линейка, циркуль, транспортир). Файл выслать в формате PDF.
Примечание: склонения звёзд δσ откладывать по обе стороны от небесного экватора QQ΄.
1.3. Положения звёзд в кульминациях.
Определить моменты времени и горизонтные координаты (z и A) в кульминациях для десяти выбранных звёзд. Оформить в виде таблицы.
Кульминация светил - прохождение светилом небесного меридиана в точке наблюдения при суточном вращении небесной сферы. За время одного оборота небесной сферы (сутки) звезда будет кульминировать дважды: один раз в точке, расположенной ближе к зениту места, т. е. в точке её верхней кульминации, другой раз - в противоположной точке - точке нижней кульминации. Например, см. рис.1. звезда
 точка a – точка верхней кульминации, точка a
точка a – точка верхней кульминации, точка a
׳ – точка нижней кульминации; звезда
 точка b – точка верхней кульминации, точка b׳ – точка нижней кульминации.
точка b – точка верхней кульминации, точка b׳ – точка нижней кульминации.1.3.1. Определение азимута светил.
Азимут светила - двугранный угол между плоскостью небесного меридиана и вертикалом светила. В точке кульминации вертикал светила совпадает с небесным меридианом. То есть для всех точек дуги меридиана ZSZ΄ азимут A=0°. Для противоположной дуги меридиана ZNZ΄ азимут A=180°.
1.3.2. Определение момента кульминации по шкале звёздного времени.
Связь между первой и второй экваториальными системами координат описывается формулой
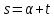 ,
,где t - часовой угол светила (двугранный угол между плоскостью небесного меридиана и плоскостью круга склонений светила). Но в момент кульминации светила круг склонения светила совпадает с небесным меридианом в точке наблюдения.
Тогда: в точке верхней кульминации
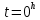 ,
, 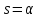 . В точке нижней кульминации
. В точке нижней кульминации 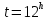 ,
, 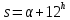 . (При необходимости вычесть 24h).
. (При необходимости вычесть 24h).1.3.3. Определение зенитного расстояния светил в кульминациях
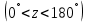 .
.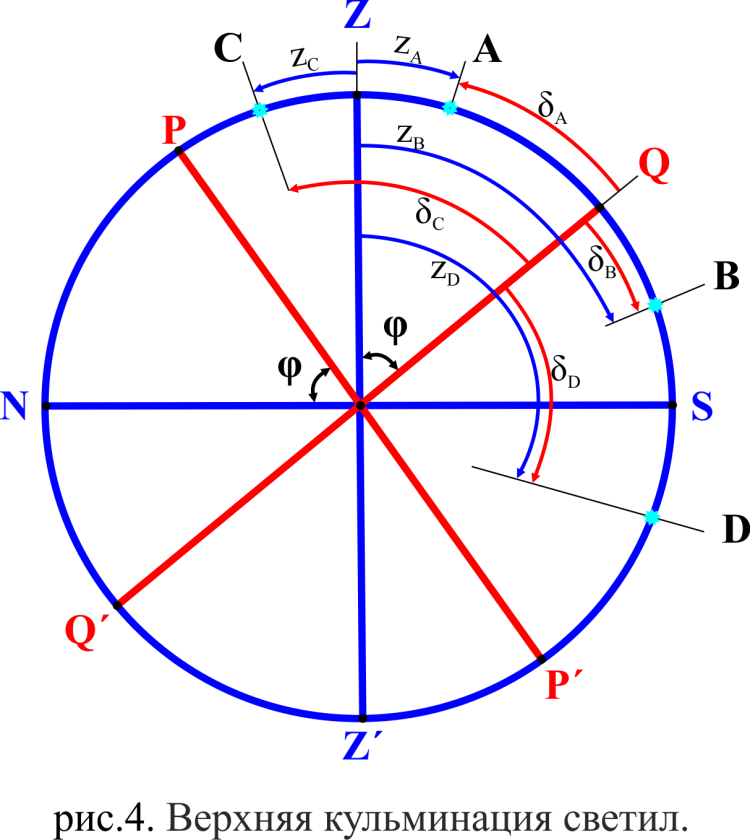 1. Если Верхняя Кульминация (ВК) светила происходит к югу от зенита Z,
1. Если Верхняя Кульминация (ВК) светила происходит к югу от зенита Z, от Z до Q (точка А на рис.4),
то
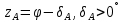 .
.2. Если ВК светила происходит
от Q до S (точка B на рис.4),
то
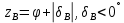 .
.3. Если ВК светила происходит
от Z до P (точка C на рис.4),
то
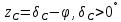 .
.4. Если ВК светила происходит
от S до P΄ (точка D на рис.4),
то