Файл: Учебнометодическое пособие по дисциплине геодезическая астрономия с основами астрометрии методические указания по выполнению контрольной работы 1 для студентов заочной формы обучения по специальности.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.12.2023

Просмотров: 140

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, .

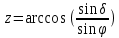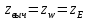Контроль выполнить по теореме синусов:

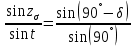, где .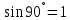

Отсюда .

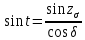Контроль должен сойтись с точностью до 0,0001.

2.3. Для двух элонгирующих звёзд вычислить момент местного звёздного времени (s) и горизонтные координаты ( 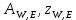) в момент их элонгации.

Для решения использовать Задание №1.

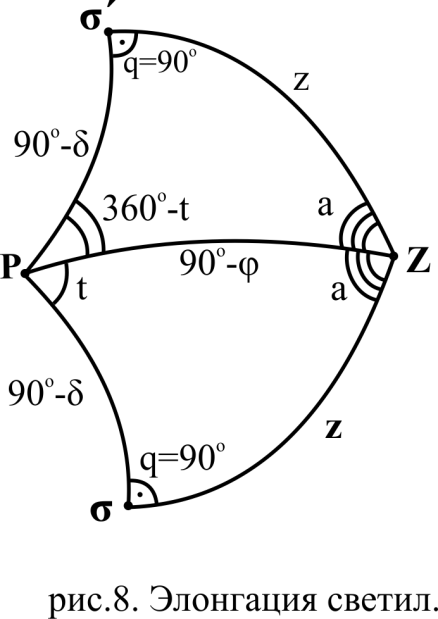
Так как известны широта точки наблюдения и экваториальные координаты и элонгирующих звёзд, то решение задачи получим из решения прямоугольного (угол q=90o) параллактического треугольника (см. рис. 8) по правилу Непера – Модюи.

  1. Часовой угол



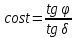
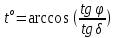
  1. моменты западной и восточной элонгаций ( и ) , .



  1. Зенитное расстояние вычислить по формуле

,

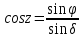
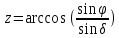
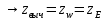
  1. Для получения азимутов звезды, соответствующих моментам элонгаций в северном полушарии, нужно для западной элонгации из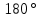 вычесть угол 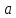, соответствующий наибольшему отклонению светила от северной части меридиана, а для восточной элонгации - прибавить угол 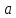к 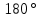. Следовательно

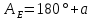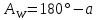; , где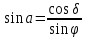

Контроль выполнить по теореме синусов: 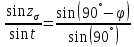, где .

Отсюда .

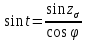Контроль должен сойтись с точностью до 0,0001.

При выполнении Задания №2 (и последующих заданий) возможно, использовать программу Exel или другую, удобную для вычислений, программу.

Пример выполнения Задания 2.1.

Вычислить моменты местного звёздного времени s и азимуты A точек восхода и захода звёзд.

Исходные данные: см. Задание №1. Вариант № = 100. Широта φ=30°00΄, АЕ 2018 г.

Условие
№ по АЕ

2018 год
Прямое восхождение α,

до 0,1m
Склонение δ,

до 0,1΄

Восходящие

и заходящие звёзды
2)
0h09,3m
+29°11,6΄

299)
12h11,1m
-22°43,3΄




№
Формулы
Звезда № 2)
Звезда № 299)

1.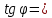


tg (30°00΄) = 0,5774
0,5774

2.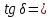


tg (+29°11,6΄) = 0,5587
- 0,4188

3.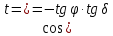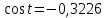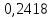






4.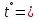


108,8191◦
76,0091◦

5.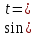


0,9465
0,9703

6.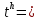


7,2546h
5,0673h

7.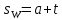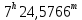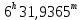






8.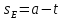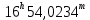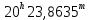






9.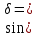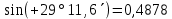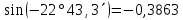






10.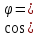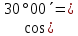


0,8660
0,8660

11.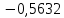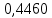






12.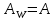


124,2784°
63,5121°

13.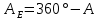


235,7216°
296,4879°

Контроль

14.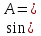


0,8263
0,8950

15.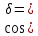


0,8730
0,9224

16.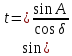


0,9465=0,9465 (из строки 5)
0,9703=0,9703


Пример выполнения Задания 2.2.

Вычислить моменты местного звёздного времени s и зенитное расстояние z двух звёзд в точках их прохождения первого вертикала.

Исходные данные: см. Задание №1. Вариант № = 100. Широта φ=30°00΄, АЕ 2018 г.

Условие
№ по АЕ

2018 год
Прямое восхождение α, до 0,1m
Склонение δ,

до 0,1΄

Звёзды, проходящие через первый вертикал над горизонтом

505)
20h40,5m
+15°58,7΄

231)
8h47,7m
+6°20,9΄




№
Формулы___Звезда_№_505)'>Формулы
Звезда № 505)
Звезда № 231)

1.


0,5774
0,5774

2.


0,2863
0,1113

3.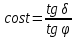


0,4959
0,1927

4.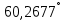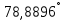






5.


0,8684
0,9813

6.


4,0178h
5,2593h

7.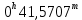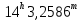






8.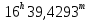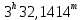






9.


0,2753
0,1106

10.


0,8660
0,8660

11.


0,5505
0,2211

12.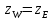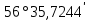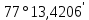






Контроль

13.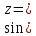


0,8347
0,9752

14.


0,8660
0,9939

15.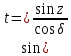


0,8684=0,8684 (из строки 5)
0,9813=0,9813

Пример выполнения Задания 2.3.

Вычислить моменты местного звёздного времени s и горизонтные координаты

( ) двух элонгирующих звёзд в момент их элонгации.

Исходные данные: см. Задание №1. Вариант № = 100. Широта φ=30°00΄, АЕ 2018 г.

Условие
№ по АЕ

2018 г.
Прямое восхождение α, до 0,1m
Склонение δ,

до 0,1΄

Элонгирующие звёзды
218)
7h56,0m
+47°30,9΄

487)
19h56,3m
+58°53,7΄




№
Формулы
Звезда № 218)
Звезда № 487)

1.


0,5774
0,5774

2.


1,0919
1,6574

3.


0,5288
0,3483

4.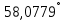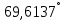






5.


0,8488
0,9374

6.


3,8719h
4,6409h

7.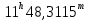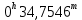






8.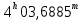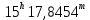






9.


0,7375
0,8562

10.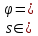


0,5000
0,5000

11.


0,6780
0,5840

12.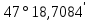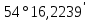






13.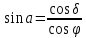


-0,7178
0,9407

14.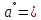


-45,8743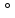

70,1632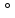

15.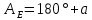


134,1257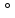

250,1632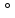

16.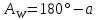


225,8743

109,8368

Контроль

13.


0,7351
0,8118

14.


0,6754
0,5166

15.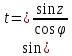


0,8488=0,8488 (из строки 5)
0,9374=0,9374

Смотрите также файлы