Файл: Учебнометодическое пособие по дисциплине геодезическая астрономия с основами астрометрии методические указания по выполнению контрольной работы 1 для студентов заочной формы обучения по специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 139
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
8. Выписка из КГЗ-2 Раздел II "Звёздные постоянные для приведения на видимое место звёзд со склонениями
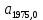" стр.96-209. Звезда (2237) -стр.154.  | +0,10052 | 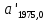 | +0,1568 |
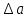 | +0,00001 | 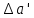 | +0,0015 |
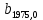 | +0,00839 | 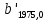 | +0,9876 |
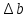 | +0,00008 | 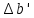 | -0,0002 |
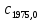 | +0,01341 | 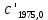 | +0,9564 |
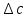 | +0,00013 | 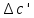 | 0 |
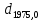 | -0,08444 | 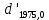 | +0,0982 |
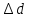 | 0 | 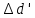 | +0,0009 |
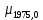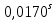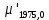 | +  |  | +0,282'' |
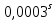 | -  |  | +0,002'' |
9. Вычислить звёздные постоянные на эпоху наблюдения t,5 (2003,5).
| Формула | Значение величины на 1975,0 | Значение поправки за переход на эпоху наблюдений | Значение величины на 2003,5 |
 | |||
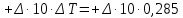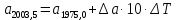 | +0,10052 | +0,00001·10·0,285=+0,00003 | +0,10055 |
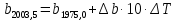 | +0,00839 | +0,00008·10·0,285=+0,00023 | +0,00862 |
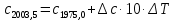 | +0,01341 | +0,00013·10·0,285=+0,00037 | +0,01378 |
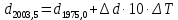 | -0,08444 | 0 | -0,08444 |
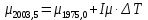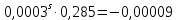 | +  | -  | +0,01691 |
| | | | |
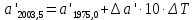 | +0,1568 | +0,0015·10·0,285=+0,0043 | 0,1611 |
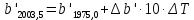 | +0,9876 | -0,0002·10·0,285=-0,0006 | 0,9870 |
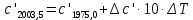 | +0,9564 | 0,0000 | +0,9564 |
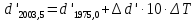 | +0,0982 | +0,0009·10·0,285=+0,0026 | 0,1008 |
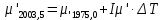 | +0,282'' | +0,002''·0,285=+0,0006 | +0,2826 |
10. Вычислить поправку за переход от средних координат
(см. п.5) к видимым координатам 
на заданный момент времени 
по формулам: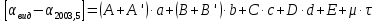
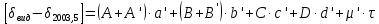
| Величина | Значение | Величина | Значение | Формула | Значение |
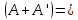 | +7,230 | 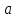 = | +0,10055 | 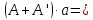 | +0,72699 |
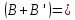 | +6,745 | 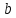 = | +0,00862 | 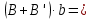 | +0,05813 |
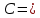 | +13,709 | 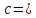 | +0,01378 | 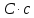 = | +0,18892 |
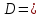 | -13,631 |  | -0,08444 | 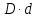 = | +1,15101 |
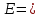 | +0,0017 | --- | --- | 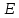 = | +0,0017 |
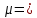 | +0,0169 | 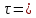 | +0,1044 | 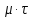 = | +0,00177 |
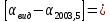 | +2,12851 | ||||
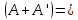| | +7,230 | 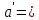 | +0,1611 | 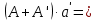 | +1,16462 |
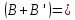| | +6,745 | 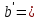 | +0,9870 | 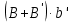 = | +6,65716 |
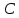 = | +13,709 | 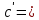 | +0,9564 | 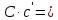 | +13,1114 |
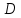 = | -13,631 | 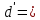 | +0,1008 | 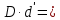 | -1,3735 |
 = | +0,288 |  = | +0,1044а | 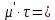 | +0,0295 |
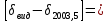 | +19,5891 | ||||
11. Вычислить видимые координаты
на заданный момент времени.по формулам:
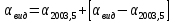
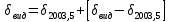
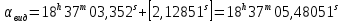
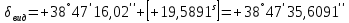
Приложение.
Основные формулы сферической тригонометрии
При решении задач сферической астрономии используются формулы сферической тригонометрии. Для того чтобы решить сферический треугольник необходимо найти все его неизвестные элементы, используя заданные (известные) элементы. Сферический треугольник считается заданным, если известны какие-либо три его элемента.
Приведённые ниже группы формул имеют преимущество, которое состоит в следующем: выбор четверти искомых углов происходит уже в решении, следовательно, отпадает необходимость анализа формулы на знаки.
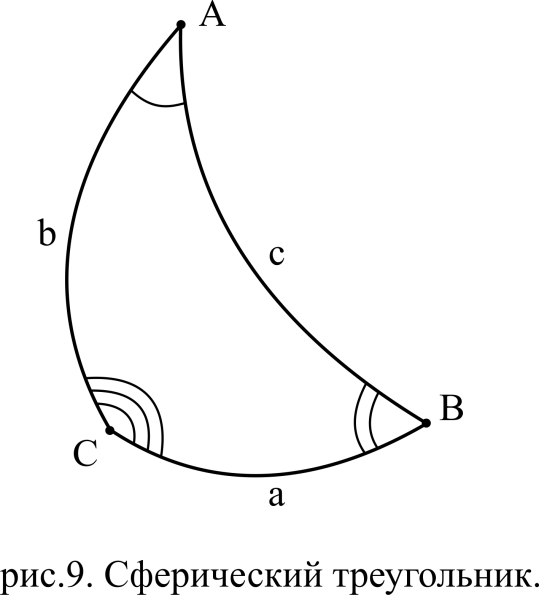
1. Формула синусов связывает между собой противолежащие элементы сферического треугольника - углы и стороны.
В сферическом треугольнике синусы сторон пропорциональны синусам противолежащих углов.
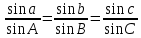
2. Формула косинуса стороны связывает между собой все три стороны и один из углов сферического треугольника.
Косинус стороны сферического треугольника равен произведению косинусов двух других сторон, сложенному с произведением синусов тех же сторон на косинус угла между ними.
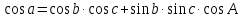
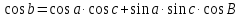
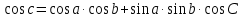
3. Формула косинуса угла связывает между собой три угла и одну из сторон сферического треугольника
Косинус угла сферического треугольника равен произведению косинусов двух других углов (взятому с обратным знаком) плюс произведение синусов тех же углов на косинус стороны между ними.
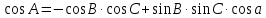
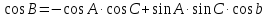
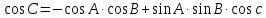
4. Формула пяти элементов.
Произведение синуса стороны на косинус прилежащего угла равно произведению косинуса противолежащей этому углу стороны на синус третьей стороны, минус произведение синуса противолежащей стороны на косинус третьей стороны и на косинус угла между ними.
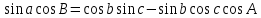
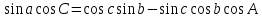
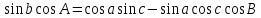
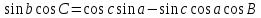
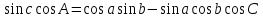
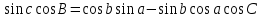
5. Формула котангенсов (четырёх элементов) связывает между собой четыре элемента сферического треугольника, лежащие рядом.
Произведение котангенса крайней стороны на синус внутренней, равно произведению косинусов внутренних элементов, сложенному с произведением
синуса внутреннего угла на котангенс крайнего.
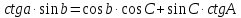
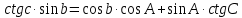
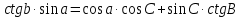
6. Правило Непера-Модюи применяется только для решения прямоугольных сферических треугольников. Решение прямоугольных треугольников проще, чем косоугольных, так как один из их элементов (угол 90°) всегда известен и для решения треугольника достаточно знать два элемента. Гипотенузой в прямоугольном сферическом треугольнике называется сторона, противолежащая прямому углу. А две другие стороны называются катетами.