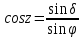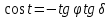Файл: Учебнометодическое пособие по дисциплине геодезическая астрономия с основами астрометрии методические указания по выполнению контрольной работы 1 для студентов заочной формы обучения по специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 136
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
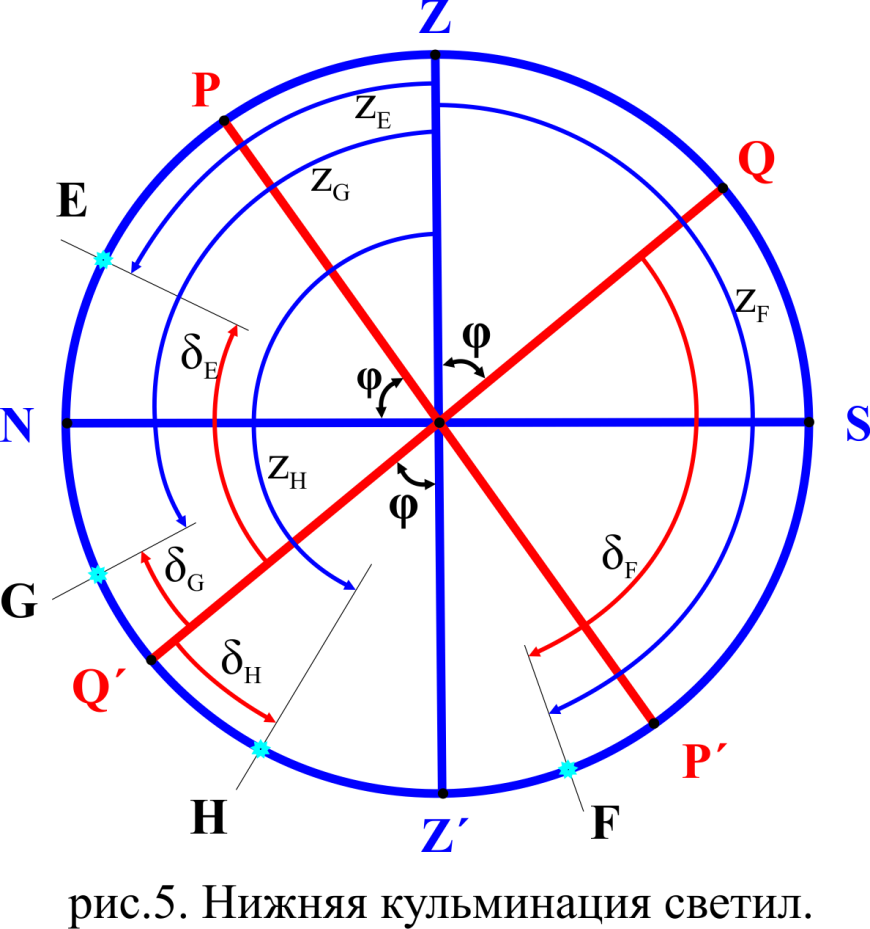 5. Если Нижняя Кульминация (НК) светила происходит
5. Если Нижняя Кульминация (НК) светила происходит от P до N (точка E на рис. 5),
то
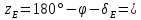
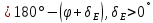
6. Если НК светила происходит
от N до Q ΄ (точка G на рис.5),
то
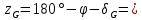
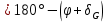 ,
, 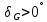 .
.7. Если НК светила происходит
от Q΄ до Z ΄ (точка H на рис.5),
то
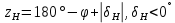 ,
,8. Если НК светила происходит
от P΄ до Z΄ (точка F на рис.5),
то
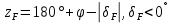 .
.Пример выполнения Задания № 1.
Исходные данные: вариант № = 100, широта
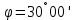 , АЕ 2018 год.
, АЕ 2018 год.п 1.1. Выборка звёзд.
| Условие | № по АЕ 2018г. | Прямое восхождение 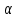 , , до 0,1m | Склонение 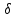 , ,до 0,1΄ |
| 1. Незаходящие звёзды  , , 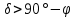 , ,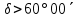 . . | 1) стр.271 | 0h41,3m | +82°35,7΄ |
| 310) стр. 264 | 12h34,3m | +69°41,2΄ | |
| 2. Невосходящие звёзды  , , 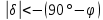 , ,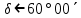 . . | 637) стр. 264 | 12h27,6m | -63°12,1΄ |
| 588) стр. 257 | 0h26,7m | -77°09,0΄ | |
| 3. Восходящие и заходящие звёзды а) 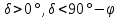 , ,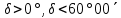 , ,б)  , , 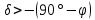 , ,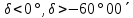 . . | 2) стр. 257 | 0h09,3m | +29°11,6΄ |
| 299) стр. 263 | 12h11,1m | -22°43,3΄ | |
| 4. Звёзды, проходящие через первый вертикал над горизонтом  , ,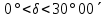 . . | 505) стр. 269 | 20h40,5m | +15°58,7΄ |
| 231) стр. 262 | 8h47,7m | +6°20,9΄ | |
| 5. Элонгирующие звёзды  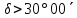 . . | 218) стр. 261 | 7h56,0m | +47°30,9΄ |
| 487) стр. 268 | 19h56,3m | +58°53,7΄ |
Примечание: 1. Номер звёзд по АЕ записывается с одной скобкой после цифр.
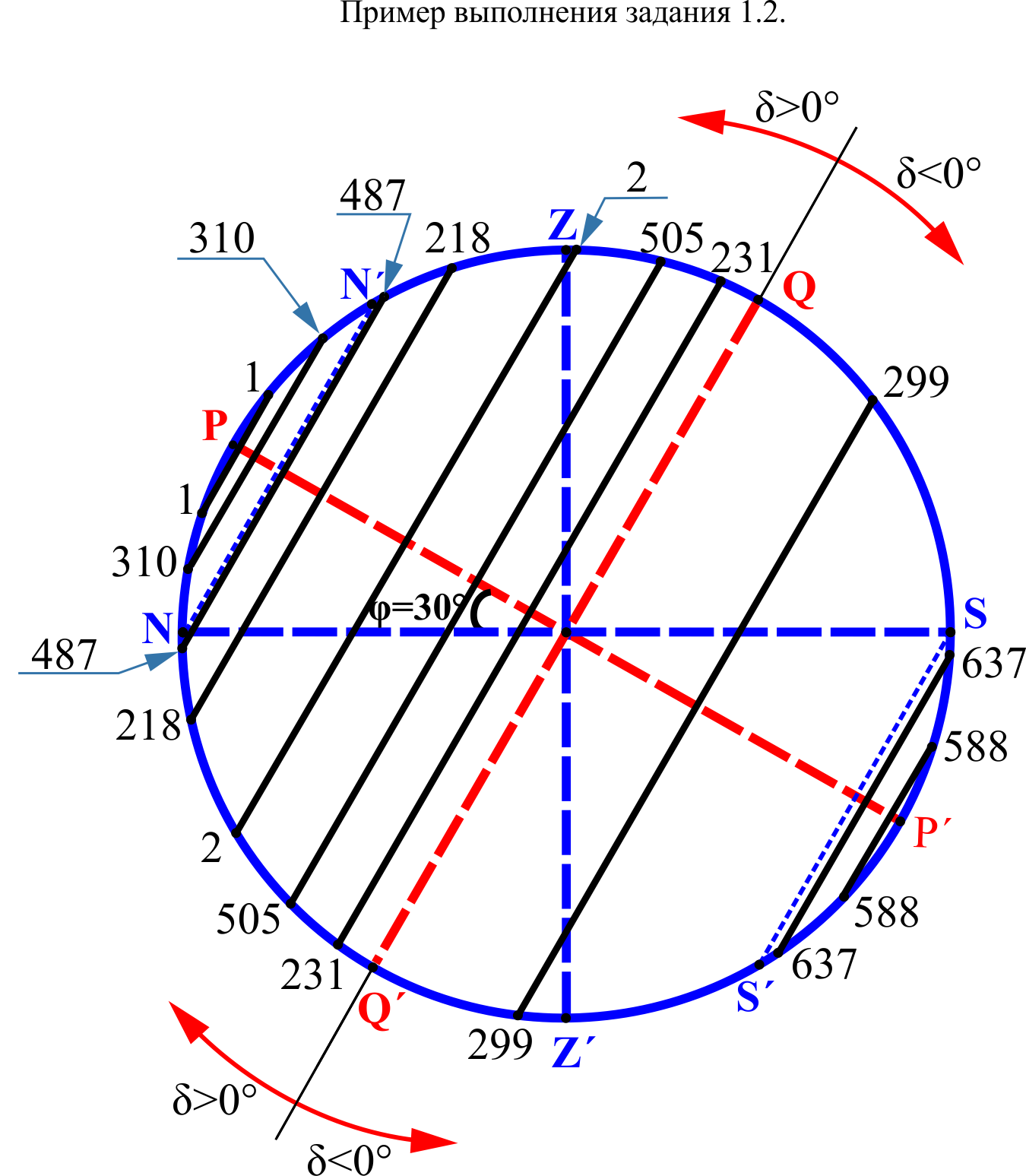
Пример выполнения 1.3.
Исходные данные: вариант № = 100, широта
 , АЕ 2018 год
, АЕ 2018 год| № звезды | Склонение δ, до 0,1΄ | Верхняя кульминация | Нижняя кульминация | ||||
| s s=α | A | z | s s=α+12h | A | z | ||
| 1) | +82°35,7΄ | 0h41,3m | 180° | z = δ - φ = 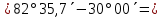 = 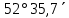 | 12h41,3m | 180° | z = 180°- (δ + φ) = 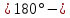 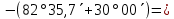 = 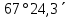 |
| 310) | +69°41,2΄ | 12h34,3m | 180° | z = δ - φ = = 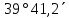 | 0h34,3m | 180° | z = 180°- (δ + φ) = = 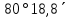 |
| 637) | -63°12,1΄ | 12h27,6m | 0° | z = φ + ⃒δ⃒= = 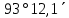 | 0h27,6m | 0° | z = 180° + φ - ⃒δ⃒= = 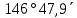 |
| 588) | -77°09,0΄ | 0h26,7m | 0° | z = φ + ⃒δ⃒= =107 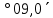 | 12h26,7m | 0° | z = 180° + φ - ⃒δ⃒= = 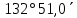 |
| 2) | +29°11,6΄ | 0h09,3m | 0° | z = φ - δ = = 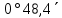 | 12h09,3m | 180° | z = 180°- (φ + δ) = = 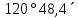 |
| 299) | -22°43,3΄ | 12h11,1m | 0° | z= φ +⃒ δ ⃒= 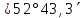 | 0h11,1m | 180° | z = 180° - φ + ⃒δ⃒= 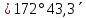 |
| 505) | +15°58,7΄ | 20h40,5m | 0° | z = φ- δ = 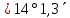 | 8h40,5m | 180° | z = 180°- φ - δ = = 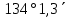 |
| 231) | +6°20,9΄ | 8h47,7m | 0° | z = φ - δ = 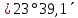 | 20h47,7m | 180° | z = 180°- φ - δ= = 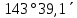 |
| 218) | +47°30,9΄ | 7h56,0m | 180° | z = δ - φ = = 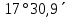 | 19h56,0m | 180° | z = 180°- φ - δ= = 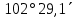 |
| 487) | +58°53,7΄ | 19h56,3m | 180° | z = δ - φ = = 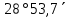 | 7h56,3m | 180° | z = 180°- φ - δ= = 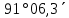 |
Задание № 2.
Решение практических задач на сфере.
2.1. Вычислить моменты местного звёздного времени s и азимуты A точек восхода и захода звёзд.
 Для решения использовать данные Задания №1. Так как известны широта
Для решения использовать данные Задания №1. Так как известны широта 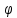 точки наблюдения и экваториальные координаты
точки наблюдения и экваториальные координаты  и
и  звезды
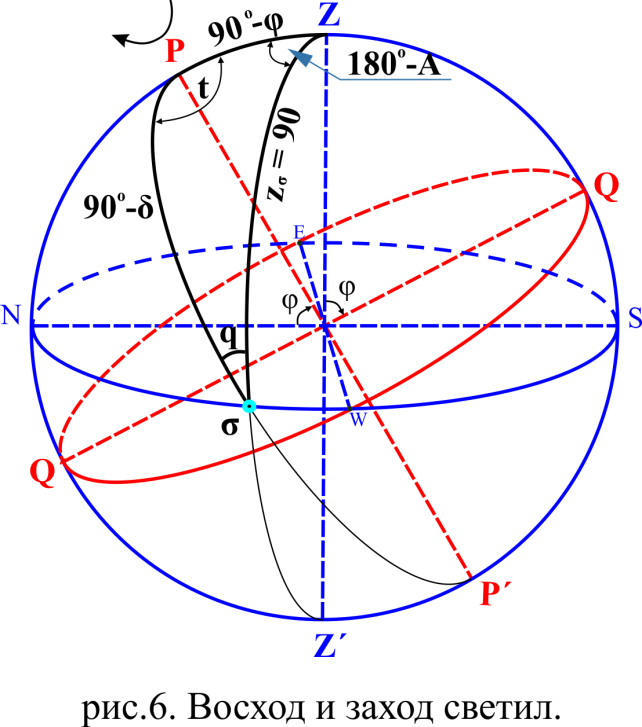
звезды 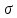 , то решение задачи получим из решения параллактического треугольника
, то решение задачи получим из решения параллактического треугольника 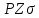 (см. рис. 6).
(см. рис. 6).Так как косинус - функция чётная, то по этой формуле найти по два значения часового угла
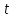 , лежащие в пределах от
, лежащие в пределах от 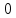 до
до 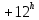 и от
и от 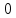 до
до 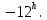 Первое значение часового угла соответствует заходу светила, второе - восходу.
Первое значение часового угла соответствует заходу светила, второе - восходу.Примечание: перевести значение часового угла t из градусной меры в часовую:
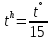 .
.-
Согласно формуле ( ) моменты восхода
) моменты восхода 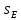 и захода
и захода 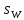 светила найти по формулам
светила найти по формулам
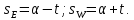
-
Определение азимутов звезды в моменты её восхода и захода.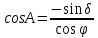
По
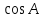
найти два значения азимута: первое соответствует восходу звезды и лежит в интервале
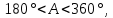 второе соответствует заходу звезды и лежит в интервале
второе соответствует заходу звезды и лежит в интервале 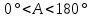 .
.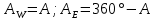 .
.Контроль выполнить по теореме синусов: в сферическом треугольнике синусы сторон пропорциональны синусам углов.
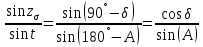 , где
, где 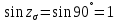 .
. Отсюда
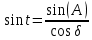 .
.Примечание: при необходимости вычесть или прибавить ± 24h или ± 60m, ±60s. Контроль должен сойтись с точностью до 0,0001.
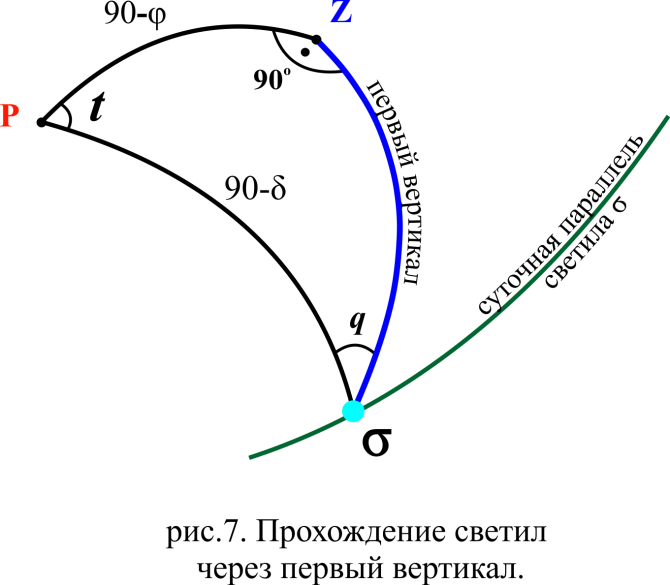
2.2. Вычислить моменты местного звёздного времени s и зенитное расстояние z двух звёзд в точках их прохождения первого вертикала.
Для решения использовать данные Задания №1. Так как известны широта
 точки наблюдения и экваториальные координаты
точки наблюдения и экваториальные координаты  и
и  звезды
звезды  , то решение задачи получим из решения прямоугольного параллактического треугольника
, то решение задачи получим из решения прямоугольного параллактического треугольника  (угол PZ
(угол PZ = 90o) (см. рис. 7) по правилу Непера – Модюи.
= 90o) (см. рис. 7) по правилу Непера – Модюи.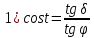
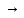
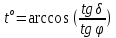
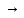

2)
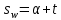 ,
, 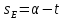
 3)
3)