ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 112
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Данные показатели используются для наглядного представления и первичного ("визуального") ана- лиза результатов измерений характеристик экспериментальной и контрольной группы.
Приведем формулы расчета основных показателей. Среднееарифметическоеxвыборки {xi}i=1…N
(выборочноесреднее) рассчитывается следующим образом19:
(1) x=1 (x1+x2 +x3 +…+xn-1
+xn) =
1
xi,
N
а выборочнаядисперсияDx:
Ni1
(2) D= 1 N ( x x)2 .
x i
N 1 i1
В компьютерной программе Microsoft Excel для Windows описательная статистика получается при- менением инструмента анализа данных "Описательная статистика" (Сервис/Анализ дан- ных/Описательная статистика). Описательная статистика для первого столбца таблицы 1 (числа пра- вильно решенных задач в контрольной группе до начала эксперимента) приведена в таблице 6.
13 Альтернативой является использование дополнительных статистических надстроек к Excel – Megastat, XLStat, которыеможно найти в свободном доступе в Интернете. В этих пакетах хорошо представлены непараметрические методы –критерийВилкоксона-Манна-Уитниидругие.
14Имеетсяввидусреднееарифметическоезначение.
15 Медианой называется значение исследуемого признака, справа и слева от которого находится одинаковое число элемен-тов выборки.
16 Модой называется такое значение измеренного признака, которым обладает максимальное число элементов выборки, тоесть значение, которое встречается в выборке наиболее часто. Например, если исследовалось число правильно решенныхучащимися задач, то модой будет такое число задач, для которого число учащихся, правильно решивших именно это числозадач, максимально.
17 Выборочная дисперсия рассчитывается как средняя сумма квадратов разностей между элементами выборки и среднимзначением. Дисперсияхарактеризуетразбросэлементоввыборкивокругсреднегозначения.
18 Гистограммой называется графическое изображение зависимости частоты попадания элементов выборки от соответ-ствующегоинтервалагруппировки(диапазоназначенийпоказателя).
n
19Символxi
i1
здесьидалееобозначаетсуммуэлементов{xi} поиндексуi,пробегающемупоследовательновсезначения
от единицы доn:x1+x2+…+xn.
Таблица6
Описательная статистика числа правильно решенных задач
в контрольной группе до начала эксперимента (см. первый столбец таблицы 1)
| Среднее | 12,6 |
| Стандартная ошибка | 0,76 |
| Медиана | 13 |
| Мода | 15 |
| Стандартное отклонение | 4,16 |
| Дисперсия выборки | 17,28 |
| Эксцесс | -0,89 |
| Асимметричность | -0,03 |
| Интервал (размах) | 15 |
| Минимум | 5 |
| Максимум | 20 |
| Сумма | 378 |
| Счет (объем выборки) | 30 |
Целый ряд приведенных в таблице 6 показателей описательной статистики педагогу-исследователю не понадобятся (далее используются только среднее (формула (1), первая строка таблицы 6), дисперсия (формула (2), шестая строка таблицы 6) и "счет" (объем выборки) – последняя строка таблицы 6). Тем не менее, мы приводим все показатели, которые автоматически выводит "Описательная статистика" в компьютерной программе Microsoft Excel для Windows (таблица 6 экспортирована из Excel), чтобы уважаемый читатель не терялся перед экраном компьютера.
Гистограмма в Excel получается применением инструмента анализа данных "Гистограмма" (Сер- вис/Анализ данных/Гистограмма). Гистограмма числа правильно решенных задач в контрольной группе до начала эксперимента (первый столбец таблицы 1) представлена на рисунке 2.
Гистограмма
 8
8Частота
6
4
2
0
5 8 11 14 17 20
Карман
Рис. 2. Гистограмма числа правильно решенных задач в контрольной группедо начала эксперимента ("частота" – число элементов выборки,попавшихвзаданныйдиапазон,называемый вExcel"карманом")
Рассмотрим теперь показатели описательной статистики для данных, измеренных в порядковой шкале.
Длярезультатовизмеренийвпорядковойшкале (задача 2.1 – см. таблицу 5) при небольшом числе градаций единственным информативным показателем описательной статистики является гистограмма20. Для визуального (качественного) сравнения экспериментальной и контрольной групп удобно стро-
ить для них совместные гистограммы. Например, по результатам таблицы 4 (см. выше) можно постро- ить несколько парных гистограмм, на которых отложены одновременно частоты для двух групп (на-
пример, контрольной и экспериментальной). На рисунках 3 и 4 приведены две из них – позволяющие сравнивать контрольную и экспериментальную группу до начала и после окончания эксперимента (на самом деле визуальный анализ не дает возможности сказать, значимо ли различаются данные выборки – для этого необходимо использовать статистические методы – см. ниже). Для их построения сначала перейдем от таблицы 4 к таблице 7, отличающейся от первой тем, что в ее ячейках стоят не абсолютное
20Есличислоградаций(различныхзначений) велико,тоинформативнымитакжеявляютсямодаимедиана.
число членов той или иной группы, набравших соответствующий балл, а доля21 (в процентах) членов группы, получивших данный балл, так как подобное преобразование (деление на одно и то же число – количество членов в данной группе) позволяет качественно сравнивать группы разных размеров (на- пример, разного количества учащихся). Затем строим гистограммы в компьютерной программе Micro- soft Excel для Windows (Меню/Вставка/Диаграмма) – см. рисунки 3 и 4, на которых по вертикали отло- жен процент членов той или иной группы, набравших соответствующий балл.
Таблица7
Результаты измерений уровня знаний в контрольной и экспериментальной группах до и после эксперимента
| Уровень знаний | Контрольная группа до на- чала экспери- мента (%) | Эксперимен- тальная группа до начала экс- перимента (%) | Контрольная группа после окончания эксперимента (%) | Эксперимен- тальная группа после оконча- ния экспери- мента (%) |
| Низкий | 30,00 | 28,00 | 40,00 | 8,00 |
| Средний | 46,67 | 48,00 | 33,33 | 52,00 |
| Высокий | 23,33 | 24,00 | 26,67 | 40,00 |
Таким образом, описательная статистика, во-первых, позволяет представить результаты педагоги- ческого эксперимента в компактном и информативном виде, что дает возможность проводить качест- венный анализ исследуемых объектов22. Во-вторых, ряд показателей описательной статистики исполь- зуется в количественном анализе (при применении статистических критериев – см. ниже).
60,00
50,00
40,00
30,00
20,00
10,00
0,00
 Низкий
НизкийСредний Высокий
 Контрольная группа до начала эксперимента (%)
Контрольная группа до начала эксперимента (%) Экспериментальная группа до начала эксперимента (%)
Экспериментальная группа до начала эксперимента (%)Рис.3.Гистограммыконтрольнойиэкспериментальнойгруппдоначала эксперимента
 60,00
60,0050,00
40,00
30,00
20,00
10,00
0,00
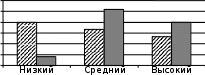
 Контрольная группа после окончания эксперимента (%)
Контрольная группа после окончания эксперимента (%) Экспериментальная группа после окончания эксперимента (%)
Экспериментальная группа после окончания эксперимента (%)Рис.4.Гистограммыконтрольнойиэкспериментальнойгрупппослеокончания эксперимента
21Доляпринимаетзначения отнулядоединицы.Дляпереходакпроцентамследуетдолюумножитьна100%.
22Показателиописательнойстатистики(объемвыборки,среднее,гистограммыит.д.) обычноприводятсявтекстедиссертационныхработиавторефератовпо педагогике.
Завершив рассмотрение показателей описательной статистики