ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «ВГТУ», ВГТУ)
ФАКУЛЬТЕТ МАШИНОСТРОЕНИЯ И АЭРОКОСМИЧЕСКОЙ
ТЕХНИКИ
Кафедра нефтегазового оборудования и транспортировки
Направление: 21.03.01 «Нефтегазовое дело»
Направленность: «Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки»
Группа: бНГД – 193
КУРСОВАЯ РАБОТА
по дисциплине «Методы и средства регистрации параметров энергетического оборудования газонефтепроводов»
Тема: Статистическая обработка результатов измерений и установление функциональной зависимости между исследуемыми величинами
Пояснительная записка
Разработал(а) В.С. Роднова
Подпись, дата Инициалы, фамилия
Руководитель Е.Е. Спицына
Подпись, дата Инициалы, фамилия
Воронеж 2021 г.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «ВГТУ», ВГТУ)
ФАКУЛЬТЕТ МАШИНОСТРОЕНИЯ И АЭРОКОСМИЧЕСКОЙ
ТЕХНИКИ
Кафедра нефтегазового оборудования и транспортировки
Направление: 21.03.01 «Нефтегазовое дело»
Направленность: «Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки»
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
по дисциплине «Методы и средства регистрации параметров энергетического оборудования газонефтепроводов»
студенту Роднова Валерия Сергеевна
группы бНГД - 193
вариант №21
(Xi=4,40мм)
Руководитель курсовой работы
СОДЕРЖАНИЕ
| | |
| Введение | 4 |
| 1. Методика обработки и анализа экспериментальных данных | 6 |
| 2. Установление минимального количества измерений | 11 |
| 3. Исключение грубых ошибок | 13 |
| 4. Методы подбора эмпирических формул | 14 |
| Заключение | 21 |
| Список литературы | 22 |
| Приложения | 23 |
ВВЕДЕНИЕ
Система доставки продукции нефтяных и газовых месторождений до потребителей представляет собой единую технологическую цепочку, в состав которой входят НПС (для нефти и нефтепродуктов) и КС (для природного газа). В связи с тем, что перекачиваемые жидкости и газы обладают массой и вязкостью, т.е. способностью оказывать сопротивление при своем перемещении, в процессе их транспортировки используют специальные энергетические системы для повышения давления нефти и газа в исходных точках магистрального трубопровода до величин, определяемых только прочностью труб и оборудования.
Еще на этапе проектирования насосного и компрессорного оборудования в обязательном порядке разрабатывают методику его испытаний, структуру определяемых количественных и (или) качественных показателей объекта, а также методы обработки и анализа экспериментальных данных.
При экспериментальном исследовании одного и того же процесса (наблюдения и измерения) повторные отсчеты на приборах, как правило, неодинаковы. Отклонения объясняются различными причинами - неоднородностью свойств изучаемого тела (материал, конструкция и т.д.), несовершенством приборов и классов их точности, субъективными особенностями экспериментатора и др. Чем больше случайных факторов, влияющих на опыт, тем больше расхождения в цифрах, получаемых при измерениях, т.е. тем больше отклонения отдельных измерений от среднего значения. Это требует повторных измерений а, следовательно, необходимо знать их минимальное количество. Кроме того, при анализе эксперимента необходимо, прежде всего, исключить грубые ошибки, появление которых ощутимо влияет на результат измерений. Однако, до того как исключить то или иное измерение, необходимо убедиться, что это действительно грубая ошибка.
После получения результатов измерений и оценки их точности, данные сводят в таблицы. Однако по табличным данным трудно установить закономерности, присущие изучаемым явлениям, поэтому на их основе подбирают алгебраические выражения, которые называют эмпирическими формулами. Такие формулы содержат постоянные величины, установленные по опытным данным, и имеют ограниченную область применения, которая не должна выходить за пределы эксперимента. Необходимость в подборе эмпирических формул также возникает при замене сложного аналитического выражения, которое требует громоздких вычислений
, упрощенной эмпирической зависимостью. Эмпирические формулы являются приближенными выражениями аналитических зависимостей. Замену точных аналитических выражений называют аппроксимацией, а функции – аппроксимирующими.
Наиболее часто в виде аппроксимирующих используют линейные, степенные, экспоненциальные и полиномные функции. Если по экспериментальным точкам можно построить несколько плавных кривых, то наилучшей будет та кривая, у которой разностные отклонения наименьшие. Наилучшие результаты при определении параметров заданного уравнения дает использование метода наименьших квадратов.
Основной целью курсовой работы является закрепление и углубление знаний, полученных студентами во время лекционных, лабораторных, практических занятий и производственной практики, а также приобретение практических навыков в работе со справочной литературой и стандартами.
Выполненная курсовая работа дает возможность объективно оценить уровень теоретической и практической подготовки студента, необходимой для его будущей инженерной деятельности.
1 Методика обработки и анализа экспериментальных данных
Общая погрешность измерений в основном определяется случайной погрешностью, учет которой очень важен. Анализ случайных погрешностей основывается на теории случайных ошибок. В основе теории случайных ошибок лежит предположение о том, что при большом числе измерений случайные погрешности одинаковой величины, но разного знака, встречаются одинаково часто. Большие погрешности встречаются реже, чем малые, или вероятность появления погрешности уменьшается с ростом ее величины. При бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений, а появление того или иного результат как случайного события описывается нормальным законом распределения.
Различают генеральную и выборочную совокупность измерений. Совокупность всех возможных значений случайной величины в рассматриваемых условиях представляет собой генеральную совокупность. Некоторая часть этих экспериментов, которая имеет место в действительных условиях, является выборочной или выборкой. Число экспериментов, составляющих выборку, представляет ее объем. Обычно считают, если число измерений n > 30, то среднее значение данной совокупности x приближается к его истинному значению.
Теория случайных ошибок позволяет решить две основные задачи: оценить точность и надежность измерения при данном количестве замеров; определить минимальное количество замеров, гарантирующее требуемую точность и надежность измерения. Наряду с этим возникает часто необходимость исключить грубые ошибки, определить достоверность полученных данных и др.
Для расчетов воспользуемся таблицами 1,2 и 3.
Таблица 1
| № измерения | Xi, мм | № измерения | Xi, мм | № измерения | Xi, мм |
| 1 | 4,40 | 14 | 4,41 | 27 | 4,43 |
| 2 | 4,38 | 15 | 4,35 | 28 | 4,40 |
| 3 | 4,49 | 16 | 4,47 | 29 | 4,50 |
| 4 | 4,31 | 17 | 4,25 | 30 | 4,33 |
| 5 | 4,23 | 18 | 4,42 | 31 | 4,23 |
| 6 | 4,44 | 19 | 4,36 | 32 | 4,36 |
| 7 | 4,37 | 20 | 4,25 | 33 | 4,41 |
| 8 | 4,25 | 21 | 4,29 | 34 | 4,41 |
| 9 | 4,46 | 22 | 4,31 | 35 | 4,48 |
| 10 | 4,40 | 23 | 4,36 | 36 | 4,26 |
| 11 | 4,28 | 24 | 4,41 | 37 | 4,46 |
| 12 | 4,43 | 25 | 4,47 | 38 | 4,39 |
| 13 | 4,50 | 26 | 4,30 | 39 | 4,38 |
Для большой выборки и нормального закона распределения характеристикой измерения являются дисперсия
Д или коэффициент вариации kв:
Д = σ2 =
 kв = σ /
kв = σ /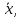 (1)
(1)где n – число измерений;
σ =
 – среднеквадратичное отклонение;
– среднеквадратичное отклонение; – среднеарифметическое значение.
– среднеарифметическое значение.Число выполненных измерений примем равным 39.

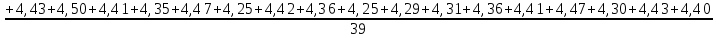
 = 4,37
= 4,37Таблица 2
| № измерения | 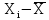 ,мм ,мм | № измерения | 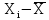 ,мм ,мм | № измерения | 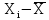 ,мм ,мм |
| 1 | 0 | 14 | 0,04 | 27 | 0,06 |
| 2 | 0,00 | 15 | -0,02 | 28 | 0 |
| 3 | 0,12 | 16 | 0,09 | 29 | 0,12 |
| 4 | -0,06 | 17 | -0,13 | 30 | -0,04 |
| 5 | -0,15 | 18 | 0,05 | 31 | -0,15 |
| 6 | 0,07 | 19 | -0,01 | 32 | -0,02 |
| 7 | 0 | 20 | -0,12 | 33 | 0,04 |
| 8 | -0,12 | 21 | -0,08 | 34 | 0,04 |
| 9 | 0,08 | 22 | -0,07 | 35 | 0,10 |
| 10 | 0,02 | 23 | -0,01 | 36 | 0 |
| 11 | -0,10 | 24 | 0,03 | 37 | 0,08 |
| 12 | 0,06 | 25 | 0,09 | 38 | 0,02 |
| 13 | 0,12 | 26 | -0,07 | 39 | 0,01 |