ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 3
| № измерения | 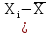 )2 ,мм )2 ,мм | № измерения | 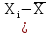 )2 ,мм )2 ,мм | № измерения | 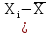 )2 ,мм )2 ,мм |
| 1 | 0 | 14 | 0,0013192 | 27 | 0,0034 |
| 2 | 0,0000 | 15 | 0,0006 | 28 | 0 |
| 3 | 0,0140 | 16 | 0,0089 | 29 | 0,0146 |
| 4 | 0,0039 | 17 | 0,0168 | 30 | 0,0019 |
| 5 | 0,0217 | 18 | 0,0021 | 31 | 0,0220 |
| 6 | 0,0045 | 19 | 0,0001 | 32 | 0,0003787 |
| 7 | 0 | 20 | 0,0155 | 33 | 0,0013 |
| 8 | 0,0152 | 21 | 0,0071 | 34 | 0,0014 |
| 9 | 0,0069 | 22 | 0,0042 | 35 | 0,0105 |
| 10 | 0,0005 | 23 | 0,0002 | 36 | 0 |
| 11 | 0,0092 | 24 | 0,0012 | 37 | 0,0068 |
| 12 | 0,0031 | 25 | 0,0084 | 38 | 0,0003 |
| 13 | 0,0155 | 26 | 0,0049 | 39 | 0,0000 |
Д = σ2 = 0,0043389
σ =
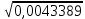 = 0,065
= 0,065kв =
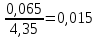
Дисперсия характеризует однородность измерения. Чем она выше, тем больше разброс. Коэффициент вариации характеризует изменчивость. Чем выше kв, тем больше изменчивость измерений относительно средних значений. Коэффициент вариации оценивает также разброс при оценке нескольких выборок.
Доверительным называется интервал значений Xi, в который попадает истинное значение
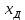 измеряемой величины с заданной вероятностью. Доверительной вероятностью измерения называется вероятность
измеряемой величины с заданной вероятностью. Доверительной вероятностью измерения называется вероятность 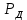 того, что значение
того, что значение 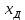 измеряемой величины попадет в данный доверительный интервал. Эта величина определяется в долях единицы или в процентах.
измеряемой величины попадет в данный доверительный интервал. Эта величина определяется в долях единицы или в процентах.Пусть необходимо установить вероятность того, что
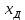 попадет в диапазон
попадет в диапазон a ≤
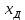 ≤ b. Доверительная вероятность
≤ b. Доверительная вероятность 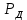 описывается выражением
описывается выражением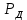 = P(a < m(x) < b) =
= P(a < m(x) < b) = 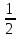 {Ф[ (b-x) / σ] - Ф[(a-x) / σ]} ,
{Ф[ (b-x) / σ] - Ф[(a-x) / σ]} ,где Ф(t) – функция Лапласа, аргументом которой является
t = μ / σ, (2)
здесь μ = (b-x); μ = - (а-x);
t – гарантийный коэффициент.
Функция Лапласа Ф(t) является интегральной, ее численные значения Ф(t) табулированы и изменяются (от t = 0 до t = 4,0) соответственно в пределах Ф(t) = 0 до Ф(t) = 0,9999.
Возможна и иная задача. На основе установленной доверительной вероятности (очень часто ее принимают равной 0,9 – 0,95) необходимо установить точность измерений, т.е. доверительный интервал 2μ.
Поскольку
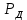 = Ф(μ / σ) , то в соответствии с приложением А обратным интерполированием можно определить половину доверительно интервала
= Ф(μ / σ) , то в соответствии с приложением А обратным интерполированием можно определить половину доверительно интервалаμ = σ ∙ arg Ф(
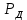 ) = σ ∙ t (3)
) = σ ∙ t (3)где t = arg Ф(
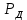 ) – аргумент функции Лапласа или при малом числе измерений
) – аргумент функции Лапласа или при малом числе измерений
(n < 10 ) аргумент функции Стьюдента, которая также табулирована в зависимости от числа измерений n и вероятности
 .
.t = argФ(0,99) = 2,625
μ = 0,076 ∙ 2,625 = 0,1995
2μ = 2 ∙ 0,1995 = 0,399
Доверительный интервал характеризует точность измерения данной выборки, а доверительная вероятность – достоверность измерения.
2. Установление минимального количества измерений
Задача сводится к установлению минимального объема выборки (числа измерений) Nmin при заданных значениях доверительного интервала 2μ и доверительной вероятности
 . При выполнении измерений необходимо знать их точность Δ, которую обычно характеризуют с помощью среднего значения среднеквадратичного отклонения σ0
. При выполнении измерений необходимо знать их точность Δ, которую обычно характеризуют с помощью среднего значения среднеквадратичного отклонения σ0 Δ =
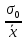 (4)
(4)где σ0 = σ /
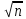 =
= 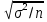 .
.σ0 =
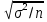 =
= 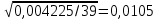
Δ =
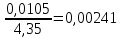
Значение σ0 также называют средней ошибкой. Доверительный интервал ошибки измерения Δ определяется аналогично тому, как и для измерений μ = t ∙ σ0 .
Зная t, по таблице легко определить доверительную вероятность ошибки измерения.
Часто возникает необходимость в определении минимального количества измерений по заданной точности и доверительной вероятности. В этом случае аналогично выражению (3) и с учетом условия (4) запишем
μ = σ ∙ arg Ф(
 ) = (σ /
) = (σ / 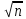 ) ∙ t . (5)
) ∙ t . (5)Отсюда, полагая Nmin = n, имеем
Nmin =
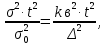 (6)
(6)где kв– коэффициент вариации, %;
Δ – точность измерения, %.
μ = (0,065 /
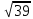 ) ∙ 2,625 = 0,027
) ∙ 2,625 = 0,027Nmin =
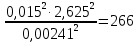
Параметр Nmin вычисляется в следующей последовательности:
-
проводят предварительный эксперимент с количеством измерений n, которое составляет в зависимости от трудоемкости опыта от 20 до 50; -
вычисляют среднеквадратичное отклонение σ = ;
; -
в соответствии с поставленными задачами эксперимента устанавливают требуемую точность измерений (μ, δ), которая должна быть не менее точности прибора; -
устанавливают нормированное отклонение t, которое также задают в зависимости от точности измерений, например, при большей точности t = 3,0, при малой – 2,0; -
из выражений (5) и (6) определяют Nmin. В дальнейшем в процессе эксперимента число измерений не должно быть меньше Nmin.
Оценки измерений с помощью σ и σ0 по приведенным методам справедливы при n> 30.
3. Исключение грубых ошибок
Появление этих ошибок ощутимо влияет на результат измерений. При анализе эксперимента необходимо, прежде всего, исключить грубые ошибки. Однако, до того как исключить то или иное измерение, необходимо убедиться, что это действительно грубая ошибка.
Известно несколько методов определения грубых ошибок статистического ряда. Наиболее простым способом исключения из ряда резко выделяющегося измерения является правило трех сигм, поскольку разброс случайных величин от среднего значения не превышает
xmax, min =
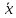 ± 3σ. (7)
± 3σ. (7)xmax = 4,35 + 3 ∙ 0,065=4,545
xmin = 4,35 - 3 ∙ 0,065=4,155
Более достоверными являются методы, базирующиеся на использовании доверительного интервала. Пусть имеется статистический ряд малой выборки, подчиняющийся закону нормального распределения. При наличии грубых ошибок критерии их появления вычисляют по формулам
β1 =
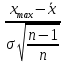 ; β2 =
; β2 = 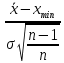 ; (8)
; (8)где xmax , xmin – наибольшее и наименьшее значения из n измерений.
β1 =
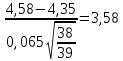
β2 =
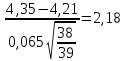
Установленные критерии сопоставляют с максимальным значением βmax, приведенным в таблице в зависимости от доверительной вероятности и числа измерений. После исключения грубых ошибок определяют новые значения
 и σ.
и σ.4. Методы подбора эмпирических формул
В процессе экспериментальных исследований получают статистический ряд измерений. Например, для функции двух переменных y = f(x) каждому значению функции y1,…,yn соответствует определенное значение аргумента x1,…,xn . На основе экспериментальных данных можно подобрать алгебраические выражения, которое называют эмпирическими формулами. Такие формулы содержат постоянные величины, установленные по опытным данным, они имеют ограниченную область применения, которая не должна выходить за пределы эксперимента. Тем не менее, эмпирические формулы имеют очень большое значение и весьма широко применяются. Необходимость в подборе эмпирических формул возникает, кроме того, при замене сложного аналитического выражения, которое требует громоздких вычислений, упрощенной эмпирической зависимостью. Часто эмпирические формулы незаменимы для анализа измеренных величин.
Таким образом, эмпирические формулы являются приближенными выражениями аналитических зависимостей. Замену точных аналитических выражений называют аппроксимацией, а функции – аппроксимирующими.
Процесс подбора эмпирических формул состоит в следующем. Вначале на сетку прямоугольных координат наносят данные измерения, соединяют точки плавной кривой, и выбираю ее вид. Вид формулы по возможности должен быть простым. Наиболее часто встречающиеся виды графиков эмпирических формул представлены на рисунке 1.
Аппроксимация экспериментальных данных прямолинейной функцией (см. рисунок 1а) позволяет наиболее просто установить эмпирическую формулу, поэтому при анализе графического материала линейную функцию часто используют. Ее также широко применяют для линеаризации кривых с помощью полу- или логарифмических координатных сеток.
Если экспериментальный график имеет вид, представленный на рисунке 1б, то необходимо применить формулу y = axb , заменяя x = lg x и, y = lg y. В результате получим y = lg a + bx, т.е. прямую на логарифмическое сетке.
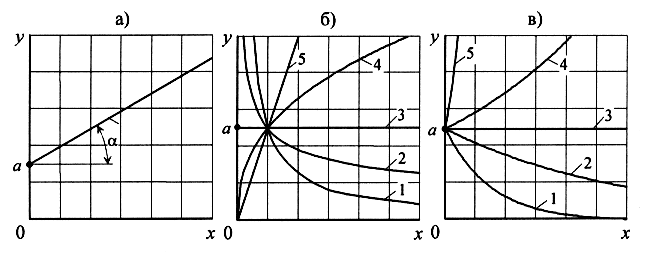
а) – линейная функция (y=a+b x, b=tg);
б) – ст