Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 264
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
z, т.е. Ez = 0; Ey ¹0; Ex ¹0. В этом случае уравнение индикатрисы принимает вид:
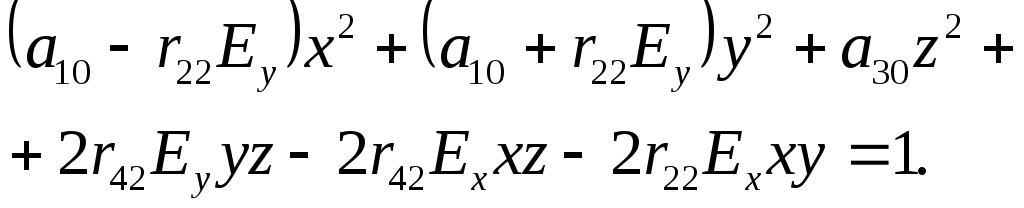 (10)
(10)
Если свет распространяется вдоль оптической оси кристалла (случай, когда поле приложено перпендикулярно направлению распространения света, называется поперечным электрооптическим эффектом), то для нахождения главных показателей преломления необходимо рассмотреть сечение оптической индикатрисы плоскостью, перпендикулярной z. Это сечение является эллипсом, удовлетворяющим уравнению:
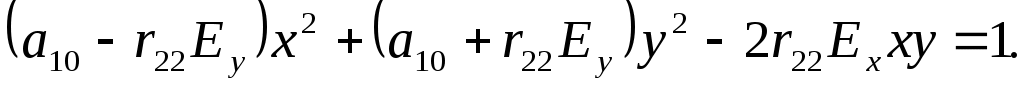 (11)
(11)
Главные оси эллипса x’, y’повернуты на угол a относительно кристаллографических осей x, y, причем
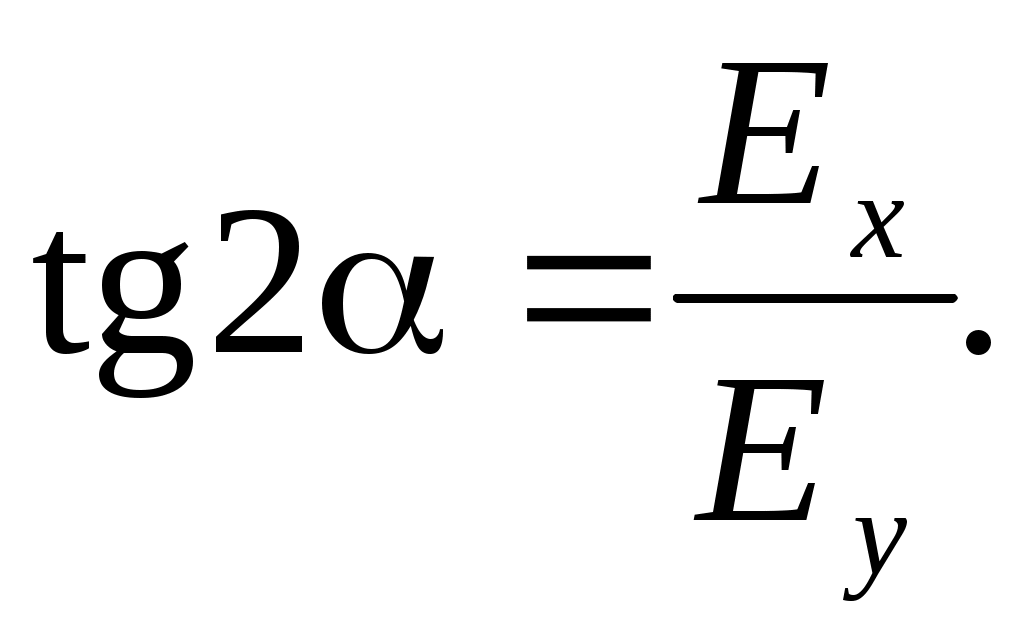 (12)
(12)
В главных осях уравнение эллипса (11) запишется в виде:
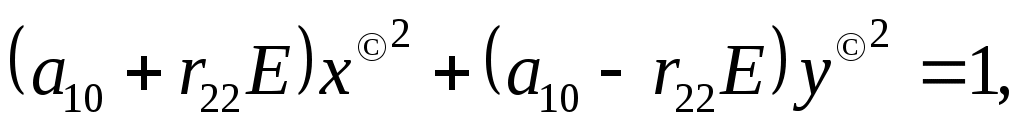 (13)
(13)
где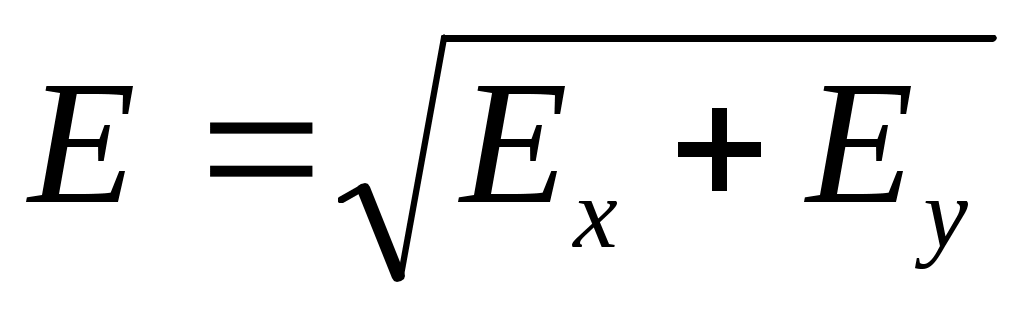 . Т.о., показатели преломления для света, поляризованного в главных направлениях, равны:
. Т.о., показатели преломления для света, поляризованного в главных направлениях, равны:
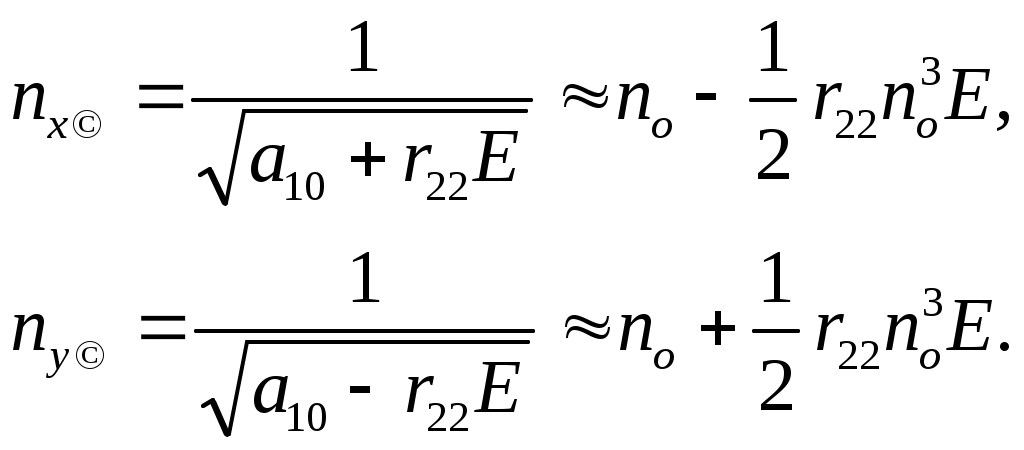 (14)
(14)
Тогда, согласно (5), разность фаз между волнами после прохождения пластинки толщиной l равна:
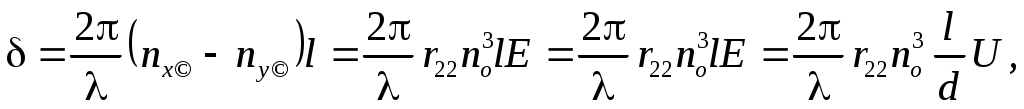 (15)
(15)
где U – приложенное напряжение; d – размеры кристалла вдоль поля. Следует отметить, что если свет распространяется не точно по оптической оси, то в (15) появляется начальный сдвиг фаз
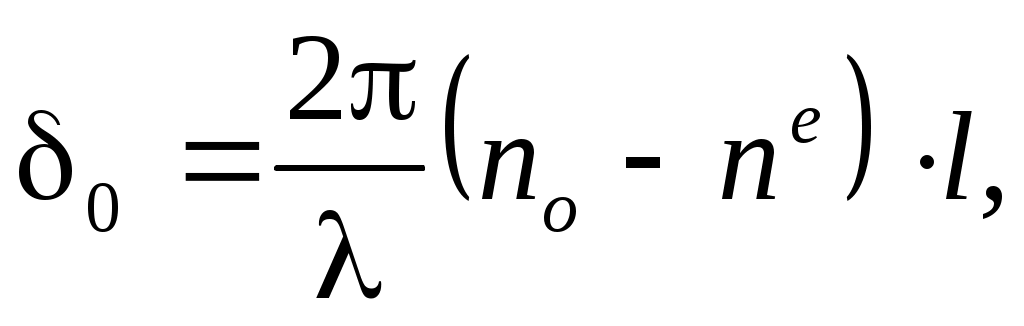 (16)
(16)
обусловленный естественной, не связанной с полем анизотропией. Индекс “е” вверху означает текущее (при произвольном угле между волной и оптической осью) значение показателя преломления для необыкновенной волны, которое может изменяться от noдо ne.
1.3. Статическая модуляционная характеристика электрооптического модулятора
Как уже указывалось, если на кристаллическую пластинку падает линейно поляризованный свет, то на выходе ее получается свет эллиптически поляризованный в общем случае. Прикладывая электрическое поле к кристаллу, мы меняем форму и ориентацию эллипса, т.е. осуществляем модуляцию света по поляризации, но интенсивность света остается неизменной. Для получения модуляции интенсивности света необходимо кристалл поместить между поляризатором и анализатором, как это показано на рис.3. Если анализатор скрещен с поляризатором, то интенсивность на выходе такого модулятора равна:
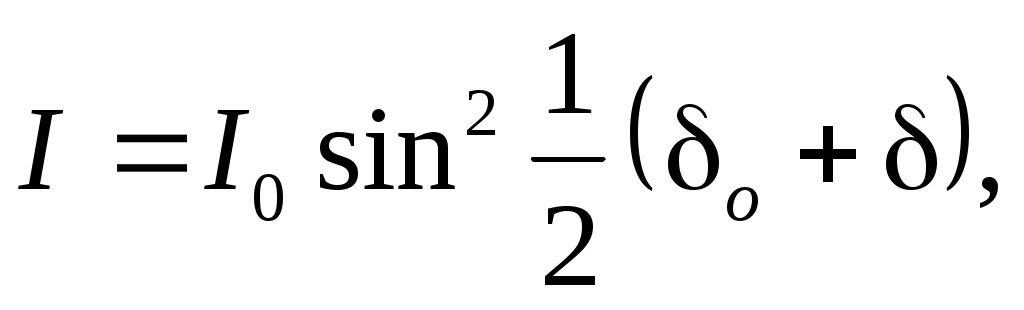 (17)
(17)
где I0 – максимальная интенсивность проходящего света.
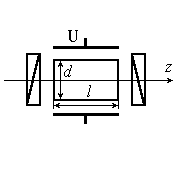
Рис. 3
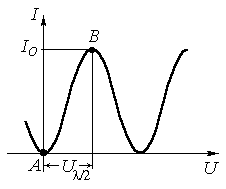
Рис. 4
Зависимость интенсивности света от статического напряжения U изображена на рис.4. Для изменения интенсивности света от нуля до максимального значения необходимо приложить к кристаллу напряжение Ul/2 . Это напряжение называется полуволновым , т.к. разность хода между обыкновенной и необыкновенной волнами в этом случае равна l/2. Из (15) нетрудно определить связь между полуволновым напряжением и параметрами кристалла:
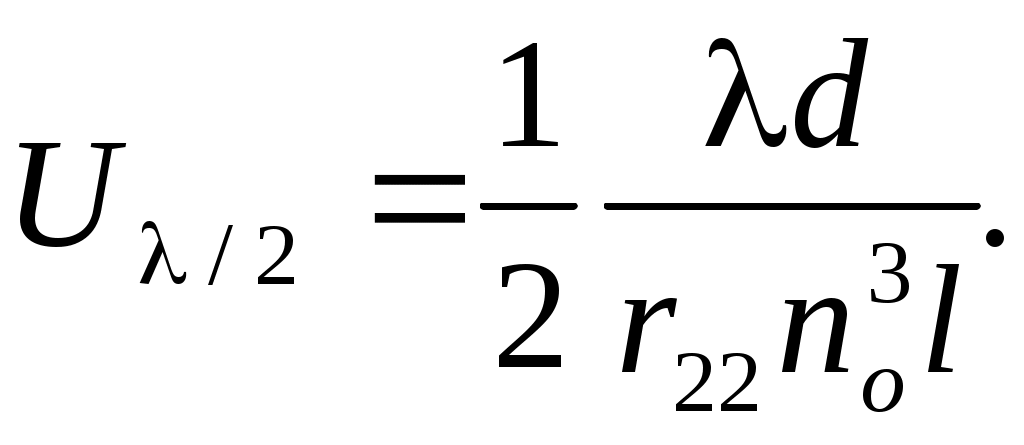 (18)
(18)
При другой конфигурации поля и осей кристалла аналогичные формулы, естественно, будут иметь иной вид.
2. Описание установки
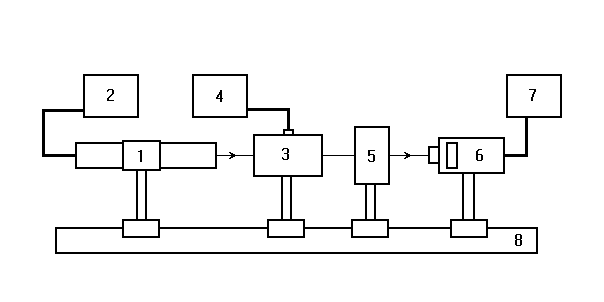
Рис. 5. Схема лабораторной установки
Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), электрооптического модулятора МЛ-5 (3) на основе кристалла LiNbO3, источника питания модулятора (4), анализатора (5), фотоприемника (6) с цифровым индикатором и блоком питания (7). Все оптические элементы размещены на оптической скамье (8). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник. Излучение лазера линейно поляризовано. Поляризатор лазера (1), модулятор (3) и анализатор (5) образуют так называемую ячейку Поккельса, позволяющую осуществлять амплитудную модуляцию прошедшего через нее света с помощью прикладываемого к модулятору напряжения от источника питания (4).
ВНИМАНИЕ ! В работе используется высокое напряжение (до 600 В). Электрооптический модулятор электрически уже соединен со своим источником питания. Студентам самостоятельно подключать или отключать разъемы модулятора и источника питания ЗАПРЕЩАЕТСЯ.
3. Порядок выполнения работы
3.1. Включить источник питания лазера и блок питания фотоприемника.
3.2. Съюстировать при необходимости все оптические элементы по лучу лазера так, чтобы луч проходил через центр всех элементов нормально к рабочим поверхностям этих элементов. Это можно проконтролировать по отражению: отраженный луч должен попадать в выходное отверстие лазера.
3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение.
3.4. Вращая оправу анализатора, определить такое положение, когда плоскость пропускания анализатора будет перпендикулярна плоскости поляризации падающего на анализатор лазерного излучения (по минимуму показаний фотоприемника).
3.5. Установить регулятор напряжения на источнике питания модулятора в крайнее левое положение. Включить источник питания модулятора.
3.6. Изменяя выходное напряжение U источника питания модулятора, снять зависимость показаний фотоприемника I от напряжения U через 20 В до 500 В (в области экстремумов зависимости – через 10 В). Измерения повторить не менее пяти раз.
3.7. Перевести регулятор напряжения на источнике питания модулятора в крайнее левое положение. Выключить все приборы.
3.8. Построить экспериментальную зависимость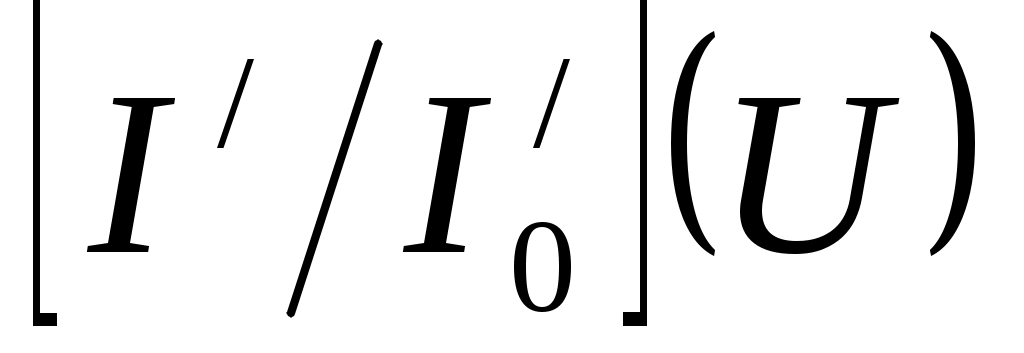 (где I/= (I – Imin), I0/= (I0 – Imin), I0 – показания фотоприемника в максимуме пропускания ячейки Поккельса, Imin – показания фотоприемника в минимуме) с учетом статистической обработки результатов с доверительной вероятностью 90%.
(где I/= (I – Imin), I0/= (I0 – Imin), I0 – показания фотоприемника в максимуме пропускания ячейки Поккельса, Imin – показания фотоприемника в минимуме) с учетом статистической обработки результатов с доверительной вероятностью 90%.
3.9. Используя определение полуволнового напряжения Ul/2, определить его значение из полученного графика.
3.10. По формуле: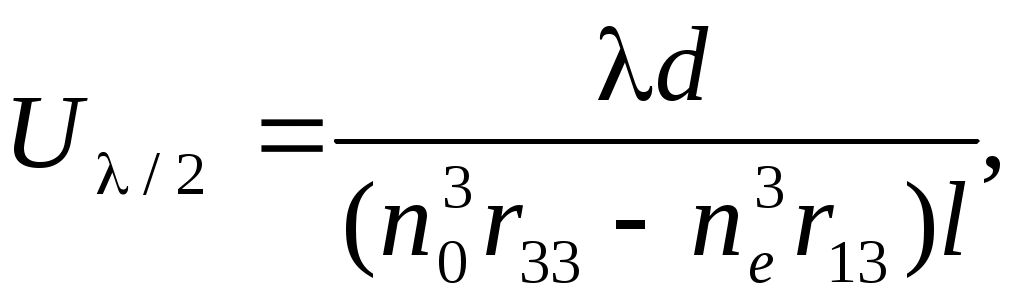 (19)
(19)
где n0 =2,2884 – обыкновенный показатель преломления кристалла; nе =2,2019 – необыкновенный показатель преломления кристалла; l – длина волны излучения лазера; r33=32,2×10-12 м/В; r13=10×10-12 м/В – электрооптические коэффициенты; d = 3 мм – толщина кристалла (расстояние между обкладками вдоль приложенного внешнего поля); l = 40 мм – длина кристалла вдоль направления луча, найти расчетное значение полуволнового напряжения для данного модулятора.
3.11. Используя полученное из эксперимента значение полуволнового напряжения, построить зависимость пропускания ячейки Поккельса от приложенного напряжения
U по формуле:

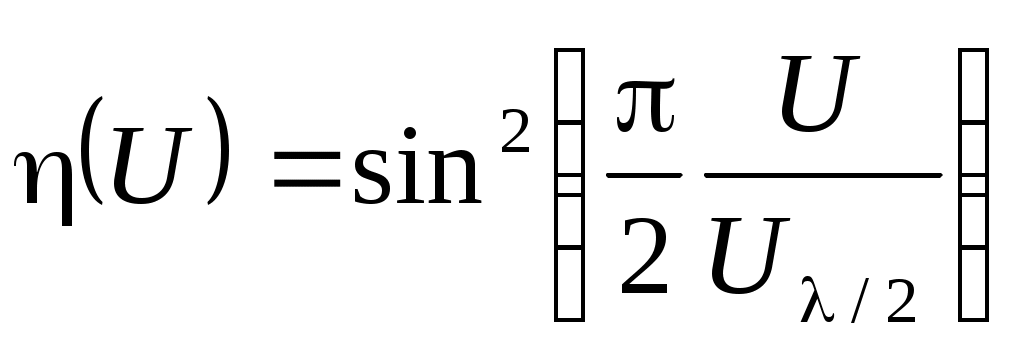 (20)
(20)
в одной координатной плоскости с экспериментальным графиком п. 3.8.
3.12. Сравнить полученные расчетные результаты с экспериментальными.
4. Контрольные вопросы и задания
Лабораторная работа
ЗАКОН МАЛЮСА
ЦЕЛЬ РАБОТЫ: ознакомление с методами получения и анализа линейно поляризованного света, работой простейших поляризационных устройств.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, поляризатор с лимбом, фотоприемник, оптическая скамья.
1. Теоретическая часть
Представление о поляризации света как его особом физическом свойстве впервые ввел И.Ньютон в 1704 г. Сам термин “
поляризация” принадлежит французскому инженеру и физику Э.Малюсу (1775–1812). Световые волны, у которых направления колебаний векторов электрического E и магнитного H полей сохраняются неизменными в пространстве или изменяются по определенному закону, называются поляризованными.
1.1. Виды поляризации световых волн
Если вектор E световой волны колеблется лишь в одной неизменной в пространстве плоскости, то такая волна называется линейно или плоско поляризованной. При линейной поляризации плоскость, содержащая волновой вектор k и вектор E, называется плоскостью колебаний или плоскостью поляризации волны.
Если же колебания вектора E совершаются так, что его конец описывает окружность в плоскости, перпендикулярной направлению распространения волны k, то такая волна называется поляризованной по кругу, еслиэллипс, то эллиптически поляризованной.
Световая волна, в которой различные направления вектора E в поперечной к направлению распространения волны плоскости равновероятны, называется естественной (естественно поляризованной или неполяризованной).
1.2. Суперпозиция двух линейно поляризованных волн [2]
Рассмотрим суперпозицию двух линейно поляризованных волн с одинаковыми частотами w, амплитудами электрических полей E1 и E2, распространяющихся в одном направлении (вдоль оси Z декартовой системы координат) со сдвигом фаз d. Пусть вектор E1 колеблется в плоскости XZ, а вектор E2 – в плоскости YZ:
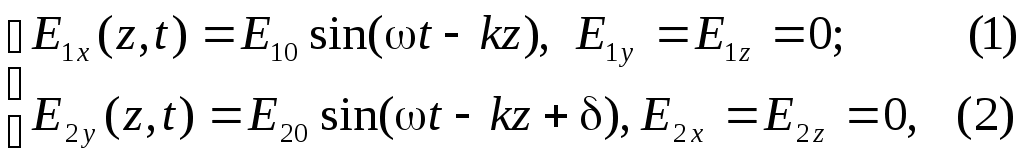
Найдем состояние поляризации суммарной волны, определяемой суперпозицией полей E ={Ex; Ey; Ez}= E1+E2, складывая покоординатно поля (1) и (2). Перепишем (2) в виде:
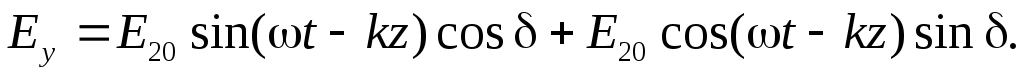 (3)
(3)
Исключая в (3) с помощью (1)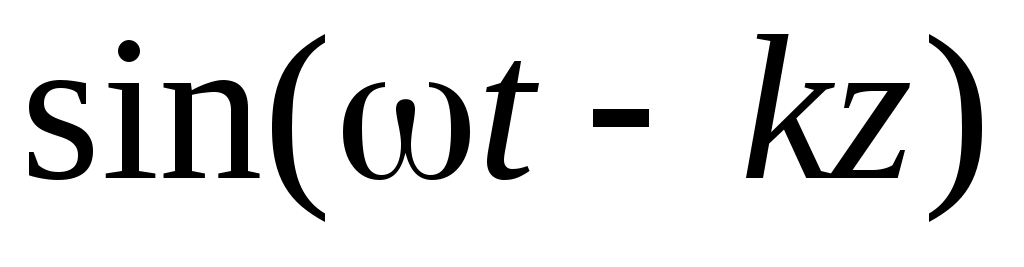 и
и 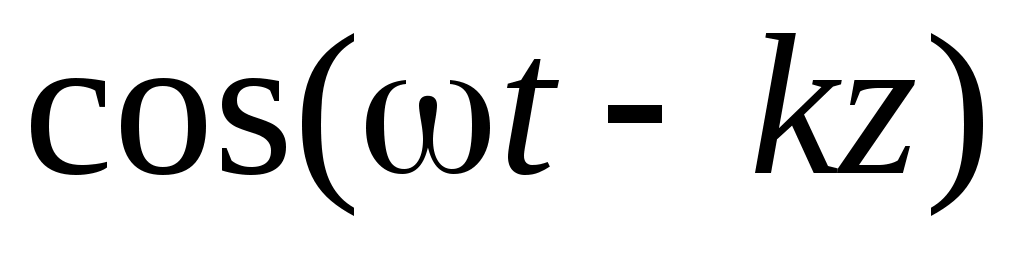 , получаем:
, получаем:
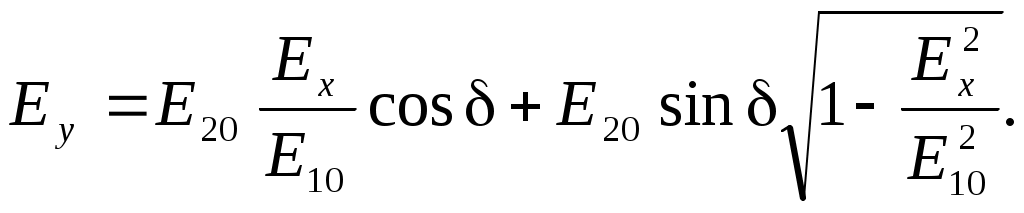 (4)
(4)
После перегруппировки получаем окончательно уравнение, описывающее состояние поляризации суммарного поля в общем виде:
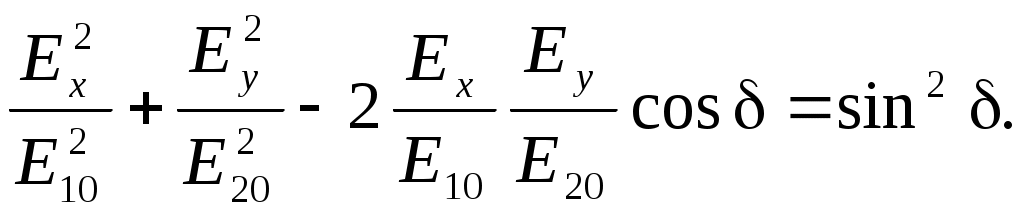
Если свет распространяется вдоль оптической оси кристалла (случай, когда поле приложено перпендикулярно направлению распространения света, называется поперечным электрооптическим эффектом), то для нахождения главных показателей преломления необходимо рассмотреть сечение оптической индикатрисы плоскостью, перпендикулярной z. Это сечение является эллипсом, удовлетворяющим уравнению:
Главные оси эллипса x’, y’повернуты на угол a относительно кристаллографических осей x, y, причем
В главных осях уравнение эллипса (11) запишется в виде:
где
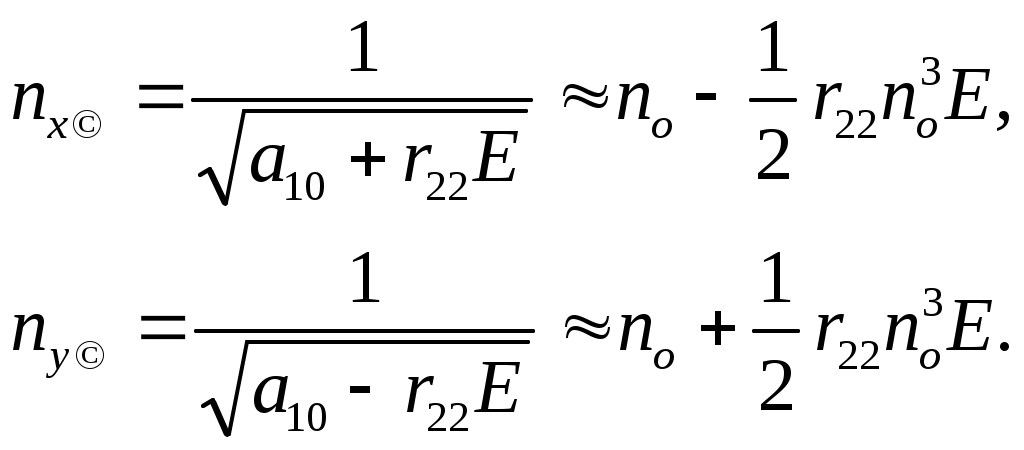 (14)
(14)Тогда, согласно (5), разность фаз между волнами после прохождения пластинки толщиной l равна:
где U – приложенное напряжение; d – размеры кристалла вдоль поля. Следует отметить, что если свет распространяется не точно по оптической оси, то в (15) появляется начальный сдвиг фаз
обусловленный естественной, не связанной с полем анизотропией. Индекс “е” вверху означает текущее (при произвольном угле между волной и оптической осью) значение показателя преломления для необыкновенной волны, которое может изменяться от noдо ne.
1.3. Статическая модуляционная характеристика электрооптического модулятора
Как уже указывалось, если на кристаллическую пластинку падает линейно поляризованный свет, то на выходе ее получается свет эллиптически поляризованный в общем случае. Прикладывая электрическое поле к кристаллу, мы меняем форму и ориентацию эллипса, т.е. осуществляем модуляцию света по поляризации, но интенсивность света остается неизменной. Для получения модуляции интенсивности света необходимо кристалл поместить между поляризатором и анализатором, как это показано на рис.3. Если анализатор скрещен с поляризатором, то интенсивность на выходе такого модулятора равна:
где I0 – максимальная интенсивность проходящего света.

Рис. 3

Рис. 4
Зависимость интенсивности света от статического напряжения U изображена на рис.4. Для изменения интенсивности света от нуля до максимального значения необходимо приложить к кристаллу напряжение Ul/2 . Это напряжение называется полуволновым , т.к. разность хода между обыкновенной и необыкновенной волнами в этом случае равна l/2. Из (15) нетрудно определить связь между полуволновым напряжением и параметрами кристалла:
При другой конфигурации поля и осей кристалла аналогичные формулы, естественно, будут иметь иной вид.
2. Описание установки

Рис. 5. Схема лабораторной установки
Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), электрооптического модулятора МЛ-5 (3) на основе кристалла LiNbO3, источника питания модулятора (4), анализатора (5), фотоприемника (6) с цифровым индикатором и блоком питания (7). Все оптические элементы размещены на оптической скамье (8). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник. Излучение лазера линейно поляризовано. Поляризатор лазера (1), модулятор (3) и анализатор (5) образуют так называемую ячейку Поккельса, позволяющую осуществлять амплитудную модуляцию прошедшего через нее света с помощью прикладываемого к модулятору напряжения от источника питания (4).
ВНИМАНИЕ ! В работе используется высокое напряжение (до 600 В). Электрооптический модулятор электрически уже соединен со своим источником питания. Студентам самостоятельно подключать или отключать разъемы модулятора и источника питания ЗАПРЕЩАЕТСЯ.
3. Порядок выполнения работы
3.1. Включить источник питания лазера и блок питания фотоприемника.
3.2. Съюстировать при необходимости все оптические элементы по лучу лазера так, чтобы луч проходил через центр всех элементов нормально к рабочим поверхностям этих элементов. Это можно проконтролировать по отражению: отраженный луч должен попадать в выходное отверстие лазера.
3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение.
3.4. Вращая оправу анализатора, определить такое положение, когда плоскость пропускания анализатора будет перпендикулярна плоскости поляризации падающего на анализатор лазерного излучения (по минимуму показаний фотоприемника).
3.5. Установить регулятор напряжения на источнике питания модулятора в крайнее левое положение. Включить источник питания модулятора.
3.6. Изменяя выходное напряжение U источника питания модулятора, снять зависимость показаний фотоприемника I от напряжения U через 20 В до 500 В (в области экстремумов зависимости – через 10 В). Измерения повторить не менее пяти раз.
3.7. Перевести регулятор напряжения на источнике питания модулятора в крайнее левое положение. Выключить все приборы.
3.8. Построить экспериментальную зависимость
3.9. Используя определение полуволнового напряжения Ul/2, определить его значение из полученного графика.
3.10. По формуле:
где n0 =2,2884 – обыкновенный показатель преломления кристалла; nе =2,2019 – необыкновенный показатель преломления кристалла; l – длина волны излучения лазера; r33=32,2×10-12 м/В; r13=10×10-12 м/В – электрооптические коэффициенты; d = 3 мм – толщина кристалла (расстояние между обкладками вдоль приложенного внешнего поля); l = 40 мм – длина кристалла вдоль направления луча, найти расчетное значение полуволнового напряжения для данного модулятора.
3.11. Используя полученное из эксперимента значение полуволнового напряжения, построить зависимость пропускания ячейки Поккельса от приложенного напряжения
U по формуле:
в одной координатной плоскости с экспериментальным графиком п. 3.8.
3.12. Сравнить полученные расчетные результаты с экспериментальными.
4. Контрольные вопросы и задания
-
Что называется оптической осью анизотропной среды? Какую поляризацию может иметь свет, распространяющийся вдоль оптической оси? -
Сколько оптических осей может существовать в кристалле? Что такое одноосные и двуосные кристаллы? -
Дайте характеристику взаимного расположения векторов электромагнитного поля для плоской волны в кристалле. -
Дайте определение обыкновенной и необыкновенной волны. Как соотносятся между собой показатели преломления этих волн? -
Что такое оптическая индикатриса кристалла? Какие характеристики можно определить с ее помощью? -
В чем заключаются электрооптические эффекты Керра и Поккельса? Чем они отличаются? -
Дайте определение полуволнового напряжения. Какие параметры влияют на его величину и какой физический смысл оно имеет? -
Выведите формулу (19). Какой конфигурации внешнего электрического поля и осей кристалла она соответствует? -
Ячейку Керра с нитробензолом поместили между двумя скрещенными поляризаторами так, что направление электрического поля Е в конденсаторе образует угол 450 с плоскостями пропускания поляризаторов. Конденсатор имеет длину l=100 мм. Через систему проходит свет с l=0,5 мкм. Имея в виду, что здесь постоянная Керра B = 2,2×10-10 см/В2 , определите число прерываний света в 1 с, если на конденсатор подать синусоидальное напряжение с частотой 10 МГц и амплитудой напряженности Em = 50 кВ/см. Постоянной Керра называется коэффициент B в формуле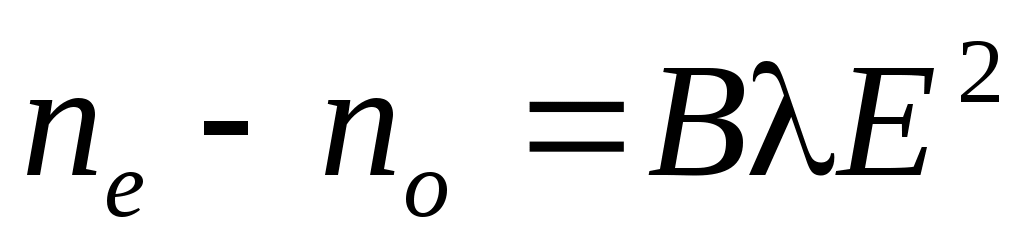 .
. -
Предложите, где на практике можно использовать электрооптический эффект.
Лабораторная работа
ЗАКОН МАЛЮСА
ЦЕЛЬ РАБОТЫ: ознакомление с методами получения и анализа линейно поляризованного света, работой простейших поляризационных устройств.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, поляризатор с лимбом, фотоприемник, оптическая скамья.
1. Теоретическая часть
Представление о поляризации света как его особом физическом свойстве впервые ввел И.Ньютон в 1704 г. Сам термин “
поляризация” принадлежит французскому инженеру и физику Э.Малюсу (1775–1812). Световые волны, у которых направления колебаний векторов электрического E и магнитного H полей сохраняются неизменными в пространстве или изменяются по определенному закону, называются поляризованными.
1.1. Виды поляризации световых волн
Если вектор E световой волны колеблется лишь в одной неизменной в пространстве плоскости, то такая волна называется линейно или плоско поляризованной. При линейной поляризации плоскость, содержащая волновой вектор k и вектор E, называется плоскостью колебаний или плоскостью поляризации волны.
Если же колебания вектора E совершаются так, что его конец описывает окружность в плоскости, перпендикулярной направлению распространения волны k, то такая волна называется поляризованной по кругу, еслиэллипс, то эллиптически поляризованной.
Световая волна, в которой различные направления вектора E в поперечной к направлению распространения волны плоскости равновероятны, называется естественной (естественно поляризованной или неполяризованной).
1.2. Суперпозиция двух линейно поляризованных волн [2]
Рассмотрим суперпозицию двух линейно поляризованных волн с одинаковыми частотами w, амплитудами электрических полей E1 и E2, распространяющихся в одном направлении (вдоль оси Z декартовой системы координат) со сдвигом фаз d. Пусть вектор E1 колеблется в плоскости XZ, а вектор E2 – в плоскости YZ:
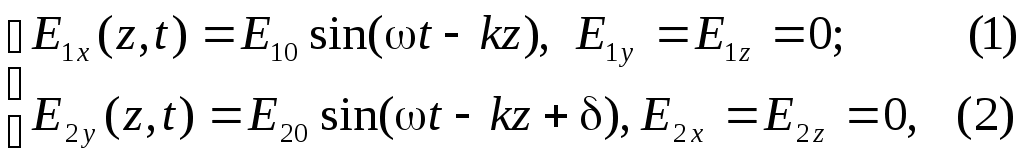
Найдем состояние поляризации суммарной волны, определяемой суперпозицией полей E ={Ex; Ey; Ez}= E1+E2, складывая покоординатно поля (1) и (2). Перепишем (2) в виде:
Исключая в (3) с помощью (1)
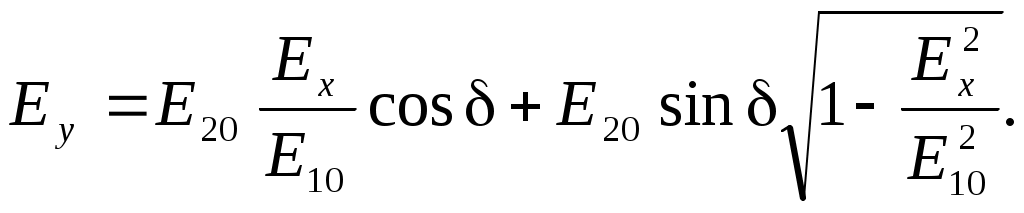 (4)
(4)После перегруппировки получаем окончательно уравнение, описывающее состояние поляризации суммарного поля в общем виде: