Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 247
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
А2 .
Расстояние f между передней главной точкой и передним фокусом называется передним фокусным расстоянием; расстояние f/между задней главной точкой и задним фокусом ‑ задним фокусным расстоянием:
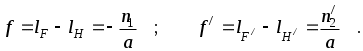 (21)
(21)
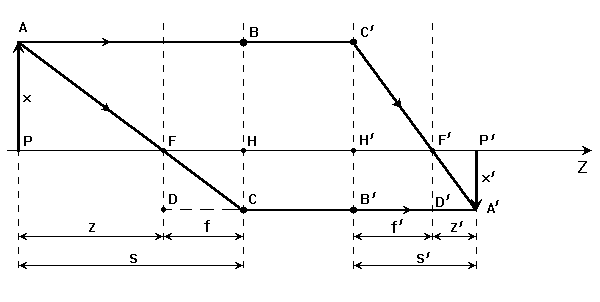
Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис.2).
Рис. 2
1.4. Уравнение линзы
Из подобия треугольников CDF, ABC, FPA (рис.5.4) следует:
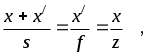 (22)
(22)
а из подобия треугольников A/D/F/, F/H/C/, A/B/C/ следует:
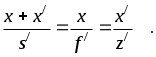 (23)
(23)
Из этих соотношений имеем: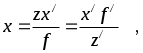 (24)
(24)
а отсюда получаем уравнение линзы в форме Ньютона:
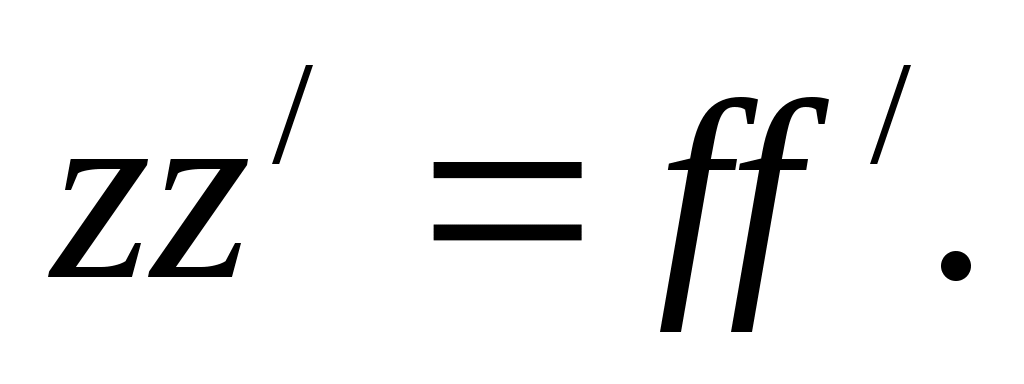 (25)
(25)
Из этих же уравнений можно получить уравнение линзы в форме Гаусса:
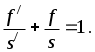 (26)
(26)
Увеличение линзы определяется из формулы:
 (27)
(27)
1.5. Тонкие линзы
Пусть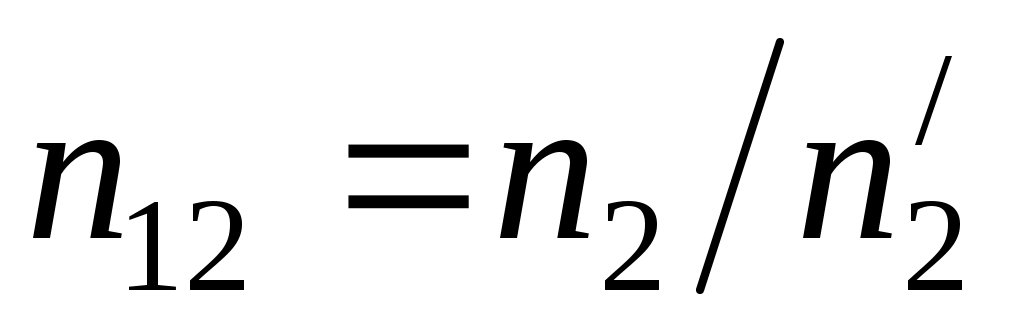 – относительный коэффициент преломления и
– относительный коэффициент преломления и 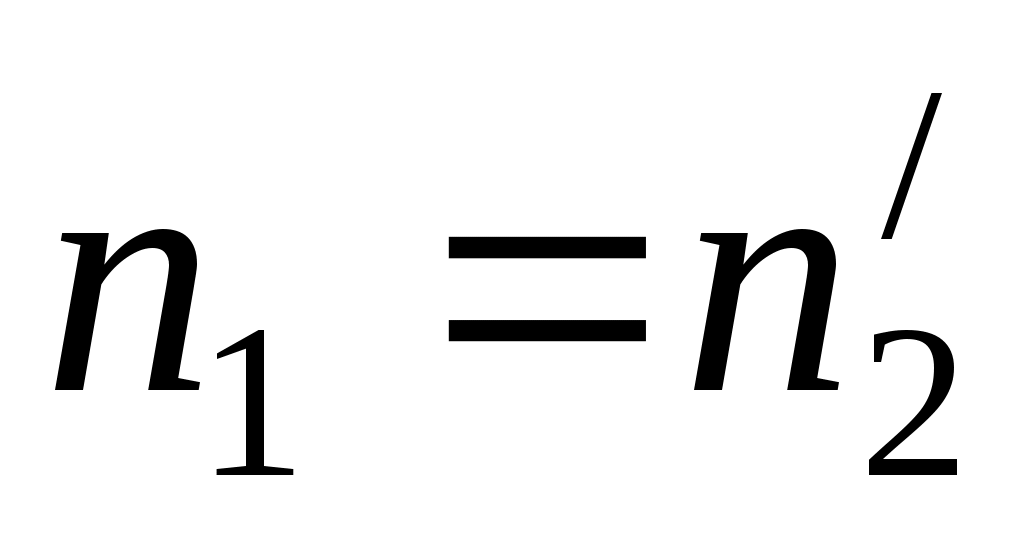 . Тогда из (12) и (21) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:
. Тогда из (12) и (21) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:
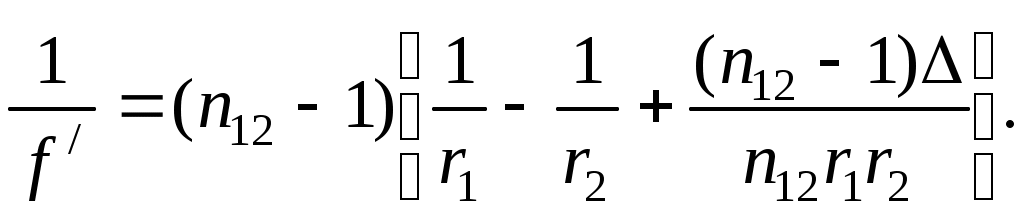 (28)
(28)
Тонкой линзой называется линза, для которой можно пренебречь третьим слагаемым в скобках (28), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:
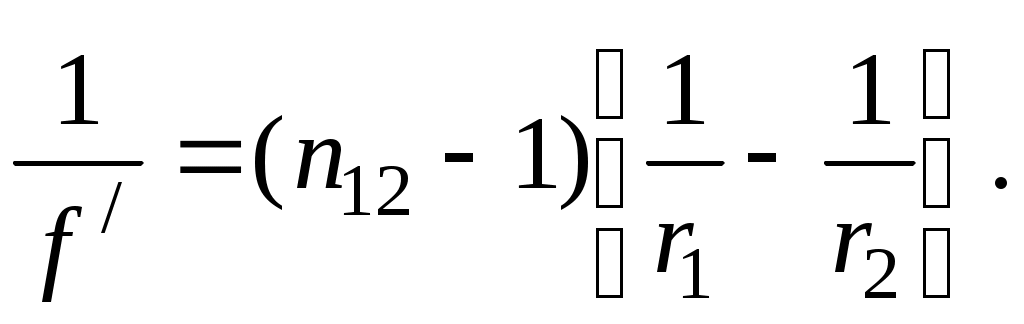 (29)
(29)
С поверхностями тонкой линзы совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:
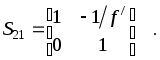 (30)
(30)
Величина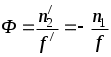 (31)
(31)
называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в воздухе 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.
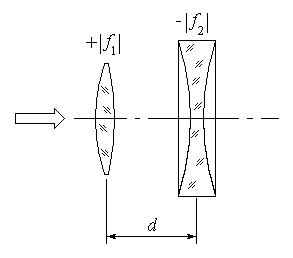 Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 3).
Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 3).
Тогда матрица S, описывающая данную систему, будет получаться путём перемножения матриц:
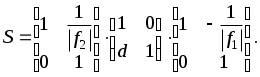 (32) Рис. 3
(32) Рис. 3
Далее находятся постоянные Гаусса, а из них кардинальные элементы данной оптической системы. Отсчет для передних главной точки и фокуса идет от первой линзы, а для задних кардинальных точек – от последней линзы по приведенному выше правилу знаков.
Примечание
При общем теоретическом введении выполнение данной лабораторной работы рекомендуется методически разбить на две последовательные части:
1. Определение фокусного расстояния тонкой линзы.
2. Определение фокусного расстояния и положения кардинальных элементов сложной оптической системы.
2. Описание лабораторных установок
2.1. Установка для измерений фокусных расстояний тонких линз
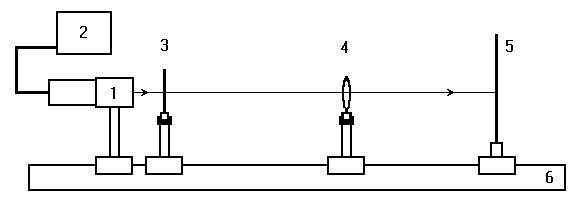
Лабораторная установка (рис.4) состоит из осветителя, включающего в себя излучатель (1) и блок питания (2) матового стекла (3) с перекрестием, играющим роль предмета, собирающей линзы (4), фокусное расстояние которой требуется определить, и экрана (5), на котором наблюдается действительное изображение предмета (3). Все элементы установлены на оптической скамье (6).
Рис. 4. Схема лабораторной установки
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте
, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана перпендикулярна оптической оси линз.
2.2. Установка для измерения положения кардинальных элементов сложной оптической системы
Лабораторная установка (рис.5) состоит из осветителя, включающего в себя излучатель (1) и блок питания (2), матового стекла (3) с перекрестием, играющим роль предмета, объектива (сложной оптической системы) (4), фокусное расстояние и положение кардинальных элементов которого требуется определить, зрительной трубы (5), настроенной на бесконечность. Все элементы установлены на оптической скамье (6). Наблюдение п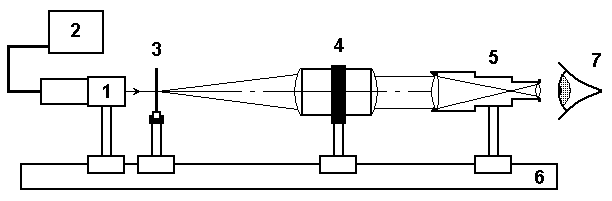 роводится глазом (7).
роводится глазом (7).
Рис. 5. Схема лабораторной установки
3. Порядок выполнения работы «Определение фокусного расстояния тонкой линзы»
3.1. Определение фокусного расстояния собирающей линзы по расстояниям от предмета до линзы и от линзы до изображения.
3.1.1. Поместив экран достаточно далеко от предмета, поместить между ними собирающую линзу и передвигать ее до тех пор, пока на экране не получится отчетливое изображение предмета (уменьшенное или увеличенное). Отсчитать по шкале линейки положения предмета, линзы и экрана.
3.1.2. Передвинуть экран и предмет в другое положение и вновь зафиксировать по шкале положения экрана, линзы и предмета.
3.1.3. Из-за неточности визуальной оценки резкости изображения измерения следует проделать не менее десяти раз. Часть измерений полезно произвести при увеличенном, а часть – при уменьшенном изображении предмета.
3.1.4. По данным каждого измерения вычислить фокусное расстояние линзы по формуле: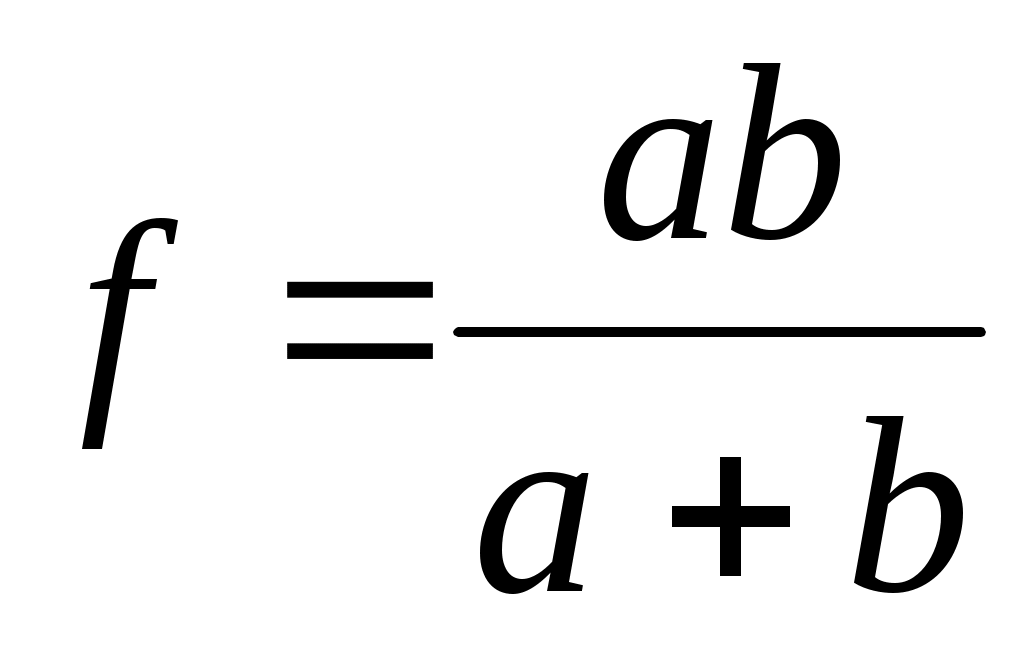 , (33)
, (33)
где а – расстояние от предмета до линзы; b – расстояние от изображения до линзы.
3.1.5. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2. Определение фокусного расстояния собирающей линзы по размерам предмета и его изображения и по расстоянию от изображения до линзы
3.2.1. Поместить собирающую линзу между предметом и экраном в таком положении, чтобы на экране появилось сильно увеличенное отчетливое изображение предмета.
3.2.2. Измерить при помощи линейки длину какого-либо штриха изображения (горизонтального или вертикального). Измерив расстояние от изображения (экрана) до линзы, найти фокусное расстояние линзы по формуле:
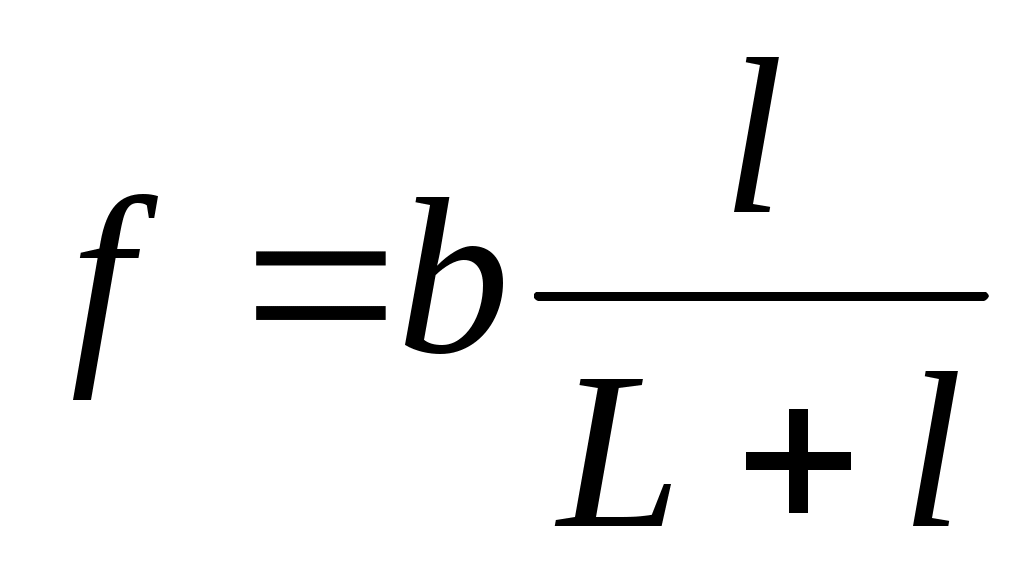 , (34)
, (34)
где b – расстояние от изображения до линзы, l – величина предмета (длина штриха предмета), L – величина изображения (длина штриха изображения).
3.2.3. Измерить расстояние от линзы до экрана не менее трёх раз. Для каждого из значений найти f. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.3. Определение фокусного расстояния собирающей линзы по величине перемещения линзы (способ Бесселя)
3.3.1. Установив предмет и экран на расстоянии А > 4f(ориентировочно значение f взять из предыдущих опытов), поместить линзу между ними и, передвигая ее, получить на экране отчетливое изображение предмета, например, увеличенное. Отсчитать по шкале положение линзы.
3.3.2. Проделать п. 3.3.1 не менее трёх раз. За положение линзы вновь принять среднее арифметическое отдельных отсчетов.
3.3.3. Передвигая линзу, получить второе отчетливое изображение предмета – уменьшенное. Снять отсчет положения линзы.
3.3.4. Проделать п. 3.3.3. не менее трёх раз. За положение линзы вновь принять среднее арифметическое отсчетов.
3.3.5. Измерить расстояние А между предметом и экраном.
3.3.6. Вычислить величину перемещения линзы l как разность отсчетов положения линзы.
3.3.7. Вычислить фокусное расстояние линзы по формуле:
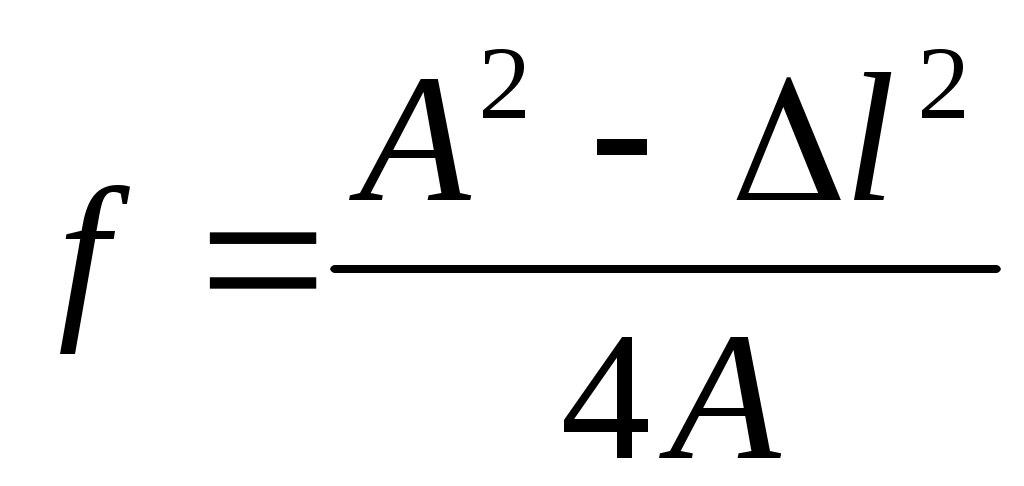 . (35)
. (35)
Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.4. Определение фокусного расстояния рассеивающей линзы
Отрицательная линза имеет мнимые фокусы. Фокусное расстояние рассеивающей линзы можно определить, если использовать действительное изображение предмета, полученное с помощью вспомогательной положительной линзы, играющее роль предмета для отрицательной линзы. Для этого необходимо использовать положительную линзу с оптической силой большей, чем модуль оптической силы исследуемой отрицательной линзы. В этом случае можно получит положительную оптическую систему, состоящую из собирающей и рассеивающей линзы.
3.4.1. Поместить между предметом и экраном собирающую линзу и получить на экране отчетливое уменьшенное изображение. Полученное с помощью собирающей линзы изображение Арбудет играть роль предмета для рассеивающей линзы (рис. 6).
3.4.2. Не убирая экрана, между ним и собирающей линзой поместить рассеивающую линзу. Замерить расстояние
b между рассеивающей линзой и экраном.
Р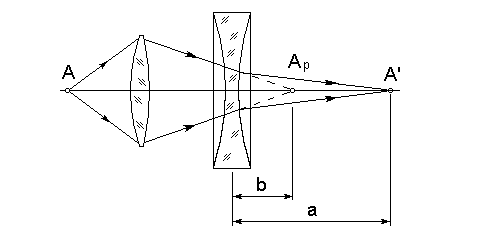
ис. 6
3.4.3. Отодвигая экран, снова добиться четкого изображения А/предмета A.
3.4.5. Замерить расстояние от рассеивающей линзы до экрана a.
3.4.6. Рассчитать модуль фокусного расстояния рассеивающей линзы по следующей формуле: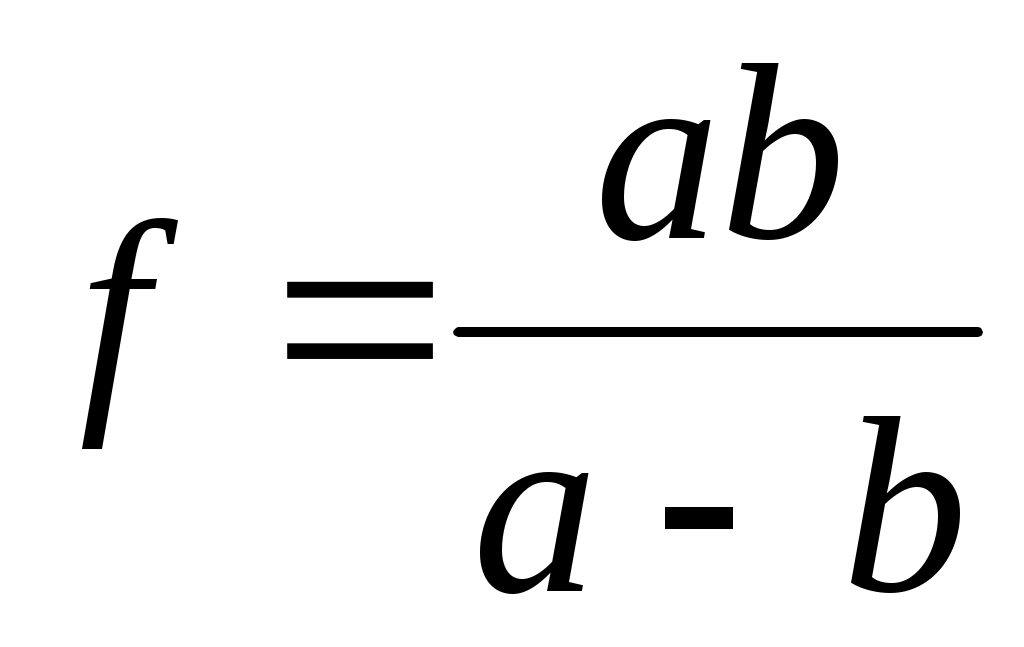 . (36)
. (36)
3.4.7. Измерения повторить не менее пяти раз. Провести статистическую обработку результатов с доверительной вероятностью 90%.
4. Порядок выполнения работы «Определение фокусного расстояния и положения кардинальных элементов сложной оптической системы»
В данной работе сначала определяется фокусное расстояние сложного объектива по способу Аббе. Затем с помощью зрительной трубы, настроенной на бесконечность, определяют положения фокусов. Отложив от фокусов отрезки, равные фокусному расстоянию, находят положение главных плоскостей.
4.1. Поместить сложный объектив между предметом и экраном.
4.2. Передвинув экран на край оптической скамьи и перемещая объектив, получить на экране сначала увеличенное изображение предмета, затем уменьшенное изображение. Определить в обоих случаях линейные увеличения изображений М1 и М2.
4.3. Измерить величину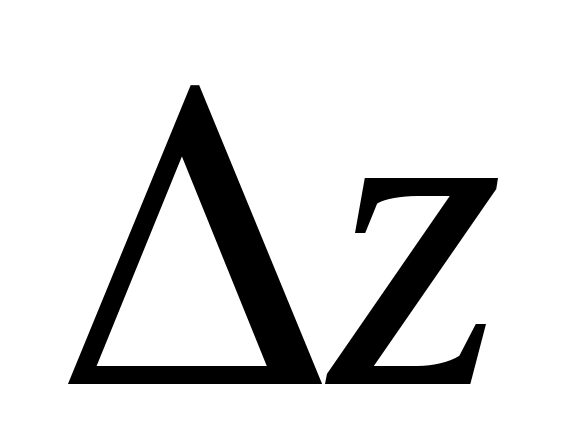 перемещения объектива из первого положения во второе.
перемещения объектива из первого положения во второе.
4.4. Рассчитать фокусное расстояние объектива по формуле:
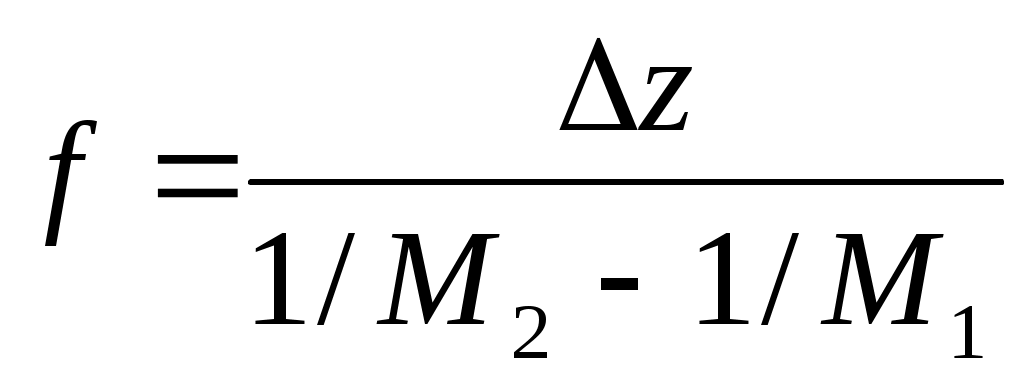 . (37)
. (37)
4.5. Убрать экран, а на его место поместить зрительную трубу, настроенную на бесконечность.
4.6. Перемещать объектив вдоль оптической скамью до тех пор, пока в поле зрения трубы не появится отчетливое изображения предмета. Измерить расстояние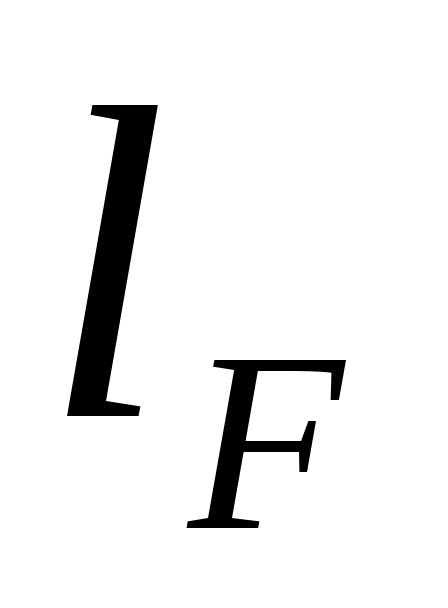 от передней преломляющей поверхности объектива по переднего главного фокуса.
от передней преломляющей поверхности объектива по переднего главного фокуса.
4.7. Перевернуть объектив на 180. Повторив п.4.6., получить расстояние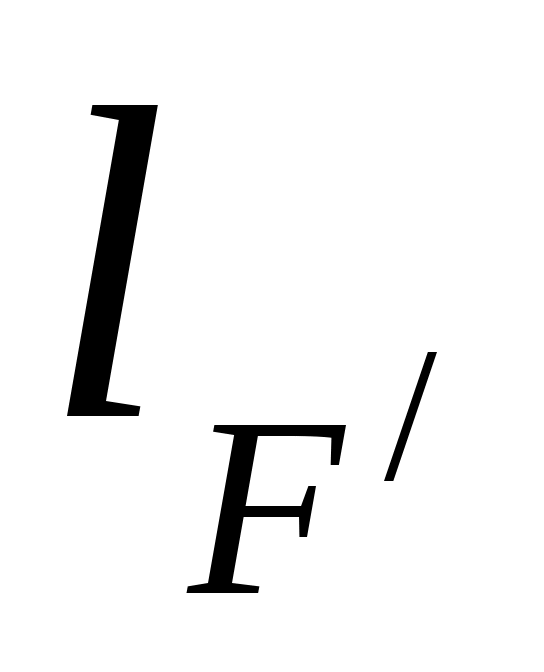
Расстояние f между передней главной точкой и передним фокусом называется передним фокусным расстоянием; расстояние f/между задней главной точкой и задним фокусом ‑ задним фокусным расстоянием:
Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис.2).
Рис. 2

1.4. Уравнение линзы
Из подобия треугольников CDF, ABC, FPA (рис.5.4) следует:
а из подобия треугольников A/D/F/, F/H/C/, A/B/C/ следует:
Из этих соотношений имеем:
а отсюда получаем уравнение линзы в форме Ньютона:
Из этих же уравнений можно получить уравнение линзы в форме Гаусса:
Увеличение линзы определяется из формулы:
1.5. Тонкие линзы
Пусть
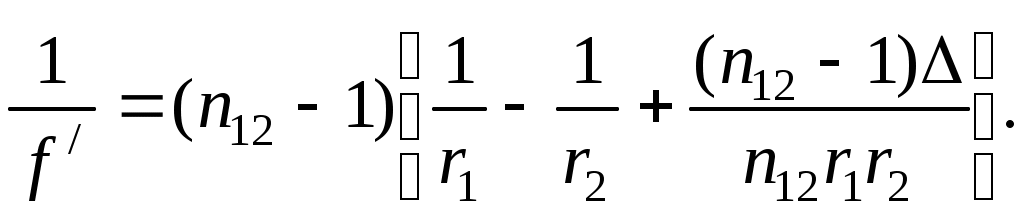 (28)
(28)Тонкой линзой называется линза, для которой можно пренебречь третьим слагаемым в скобках (28), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:
С поверхностями тонкой линзы совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:
Величина
называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в воздухе 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.
 Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 3).
Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 3). Тогда матрица S, описывающая данную систему, будет получаться путём перемножения матриц:
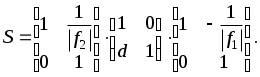 (32) Рис. 3
(32) Рис. 3Далее находятся постоянные Гаусса, а из них кардинальные элементы данной оптической системы. Отсчет для передних главной точки и фокуса идет от первой линзы, а для задних кардинальных точек – от последней линзы по приведенному выше правилу знаков.
Примечание
При общем теоретическом введении выполнение данной лабораторной работы рекомендуется методически разбить на две последовательные части:
1. Определение фокусного расстояния тонкой линзы.
2. Определение фокусного расстояния и положения кардинальных элементов сложной оптической системы.
2. Описание лабораторных установок
2.1. Установка для измерений фокусных расстояний тонких линз

Лабораторная установка (рис.4) состоит из осветителя, включающего в себя излучатель (1) и блок питания (2) матового стекла (3) с перекрестием, играющим роль предмета, собирающей линзы (4), фокусное расстояние которой требуется определить, и экрана (5), на котором наблюдается действительное изображение предмета (3). Все элементы установлены на оптической скамье (6).
Рис. 4. Схема лабораторной установки
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте
, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана перпендикулярна оптической оси линз.
2.2. Установка для измерения положения кардинальных элементов сложной оптической системы
Лабораторная установка (рис.5) состоит из осветителя, включающего в себя излучатель (1) и блок питания (2), матового стекла (3) с перекрестием, играющим роль предмета, объектива (сложной оптической системы) (4), фокусное расстояние и положение кардинальных элементов которого требуется определить, зрительной трубы (5), настроенной на бесконечность. Все элементы установлены на оптической скамье (6). Наблюдение п
 роводится глазом (7).
роводится глазом (7).Рис. 5. Схема лабораторной установки
3. Порядок выполнения работы «Определение фокусного расстояния тонкой линзы»
3.1. Определение фокусного расстояния собирающей линзы по расстояниям от предмета до линзы и от линзы до изображения.
3.1.1. Поместив экран достаточно далеко от предмета, поместить между ними собирающую линзу и передвигать ее до тех пор, пока на экране не получится отчетливое изображение предмета (уменьшенное или увеличенное). Отсчитать по шкале линейки положения предмета, линзы и экрана.
3.1.2. Передвинуть экран и предмет в другое положение и вновь зафиксировать по шкале положения экрана, линзы и предмета.
3.1.3. Из-за неточности визуальной оценки резкости изображения измерения следует проделать не менее десяти раз. Часть измерений полезно произвести при увеличенном, а часть – при уменьшенном изображении предмета.
3.1.4. По данным каждого измерения вычислить фокусное расстояние линзы по формуле:
где а – расстояние от предмета до линзы; b – расстояние от изображения до линзы.
3.1.5. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2. Определение фокусного расстояния собирающей линзы по размерам предмета и его изображения и по расстоянию от изображения до линзы
3.2.1. Поместить собирающую линзу между предметом и экраном в таком положении, чтобы на экране появилось сильно увеличенное отчетливое изображение предмета.
3.2.2. Измерить при помощи линейки длину какого-либо штриха изображения (горизонтального или вертикального). Измерив расстояние от изображения (экрана) до линзы, найти фокусное расстояние линзы по формуле:
где b – расстояние от изображения до линзы, l – величина предмета (длина штриха предмета), L – величина изображения (длина штриха изображения).
3.2.3. Измерить расстояние от линзы до экрана не менее трёх раз. Для каждого из значений найти f. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.3. Определение фокусного расстояния собирающей линзы по величине перемещения линзы (способ Бесселя)
3.3.1. Установив предмет и экран на расстоянии А > 4f(ориентировочно значение f взять из предыдущих опытов), поместить линзу между ними и, передвигая ее, получить на экране отчетливое изображение предмета, например, увеличенное. Отсчитать по шкале положение линзы.
3.3.2. Проделать п. 3.3.1 не менее трёх раз. За положение линзы вновь принять среднее арифметическое отдельных отсчетов.
3.3.3. Передвигая линзу, получить второе отчетливое изображение предмета – уменьшенное. Снять отсчет положения линзы.
3.3.4. Проделать п. 3.3.3. не менее трёх раз. За положение линзы вновь принять среднее арифметическое отсчетов.
3.3.5. Измерить расстояние А между предметом и экраном.
3.3.6. Вычислить величину перемещения линзы l как разность отсчетов положения линзы.
3.3.7. Вычислить фокусное расстояние линзы по формуле:
Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.4. Определение фокусного расстояния рассеивающей линзы
Отрицательная линза имеет мнимые фокусы. Фокусное расстояние рассеивающей линзы можно определить, если использовать действительное изображение предмета, полученное с помощью вспомогательной положительной линзы, играющее роль предмета для отрицательной линзы. Для этого необходимо использовать положительную линзу с оптической силой большей, чем модуль оптической силы исследуемой отрицательной линзы. В этом случае можно получит положительную оптическую систему, состоящую из собирающей и рассеивающей линзы.
3.4.1. Поместить между предметом и экраном собирающую линзу и получить на экране отчетливое уменьшенное изображение. Полученное с помощью собирающей линзы изображение Арбудет играть роль предмета для рассеивающей линзы (рис. 6).
3.4.2. Не убирая экрана, между ним и собирающей линзой поместить рассеивающую линзу. Замерить расстояние
b между рассеивающей линзой и экраном.
Р

ис. 6
3.4.3. Отодвигая экран, снова добиться четкого изображения А/предмета A.
3.4.5. Замерить расстояние от рассеивающей линзы до экрана a.
3.4.6. Рассчитать модуль фокусного расстояния рассеивающей линзы по следующей формуле:
3.4.7. Измерения повторить не менее пяти раз. Провести статистическую обработку результатов с доверительной вероятностью 90%.
4. Порядок выполнения работы «Определение фокусного расстояния и положения кардинальных элементов сложной оптической системы»
В данной работе сначала определяется фокусное расстояние сложного объектива по способу Аббе. Затем с помощью зрительной трубы, настроенной на бесконечность, определяют положения фокусов. Отложив от фокусов отрезки, равные фокусному расстоянию, находят положение главных плоскостей.
4.1. Поместить сложный объектив между предметом и экраном.
4.2. Передвинув экран на край оптической скамьи и перемещая объектив, получить на экране сначала увеличенное изображение предмета, затем уменьшенное изображение. Определить в обоих случаях линейные увеличения изображений М1 и М2.
4.3. Измерить величину
4.4. Рассчитать фокусное расстояние объектива по формуле:
4.5. Убрать экран, а на его место поместить зрительную трубу, настроенную на бесконечность.
4.6. Перемещать объектив вдоль оптической скамью до тех пор, пока в поле зрения трубы не появится отчетливое изображения предмета. Измерить расстояние
4.7. Перевернуть объектив на 180. Повторив п.4.6., получить расстояние